斯特林制冷机用直线电机设计与测试

郑文鹏，张 洲，苏 伟，鲁 华

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引言

随着空间技术的发展，直线式斯特林制冷机在卫星探测、遥感、通信等空间环境有越来越多的应用［1］。直线式斯特林制冷机由直线电机驱动，压缩机和直线电机一体化设计，采用非接触式气体动密封，具有体积小、重量轻、寿命长的特点，特别适用于空间环境。按照直线电机运动部件的不同，可分为动圈式、动磁式等结构。文献［2］中给出了这两种结构的主要技术对比，尽管动磁式直线电机存在单边拉力大、技术难度高等问题，但与动圈式相比，动磁式结构具有推力大、引线简单、污染小、效率高等一系列优点，动圈式直线电机有逐渐被动磁式直线电机取代的趋势。

1 动磁式直线电机结构及主要尺寸估算

1.1 动磁式直线电机结构特点

动磁式直线电机主要由定子和动子两部分构成，其中定子部分主要为线圈和外铁心(定子磁轭)，动子部分一般包括磁钢和内铁心(动子磁轭)。根据定子和动子的结构，直线电机可进一步分为很多种［3］，且分别具有不同的特点。图1为其中一种双磁钢、径向充磁的电机结构示意图。按斯特林制冷机用直线电机的结构，电机磁路为轴对称结构。由于电机的这种对称性，通过在rz坐标平面内建立的二维模型绕z轴旋转一周，即可得到电机的整体三维模型。图1中虚线表示磁路主回路示意图。

图1 动磁式直线电机结构示意图

1.2 主要尺寸估算

电机的主要尺寸与电机的最大输入功率、行程、频率及效率等参数有关。为简化分析，在估算电机主要尺寸之前，先进行如下假设:(1)电机的电压、电流均为正弦，电机功率因数为1;(2)忽略电机铁耗及其他杂散损耗;(3)气隙磁密均匀分布，忽略端部漏磁;(4)电机速度轨迹为正弦，超前位移90°电角度;(5)忽略线圈绝缘厚度。

电机的最大输入功率为

式中:umax——电机最大输入电压;

imax——最大电流。

电机的电压平衡方程为

式中:R——线圈电阻;

e——电机反电势。

反电势最大值计算公式为

式中:D——气隙平均直径，D≈(D1+D2)/2;

N′——线圈有效匝数;

B——气隙磁密径向分量幅值;

f——直线电机频率，即压缩机频率;

s——直线电机动子行程(动子单向运行最大距离)。

有效匝数N′按式(4)计算:

式中:N——线圈实际匝数;

γ——有效线圈系数，是磁钢轴向长度和线圈轴向长度的比值(见图1)，即γ=bPM/bc(动磁式电机γ＜1，动圈式电机γ=1)。

一般情况下，bPM和bc满足式(5):

则有效线圈系数可表示为

电机最大电流和最大功率之间满足式(7):

式中:η——最大功率时电机的效率。

电机的最大电流除了受电机效率影响外，还受允许的电流密度限制:

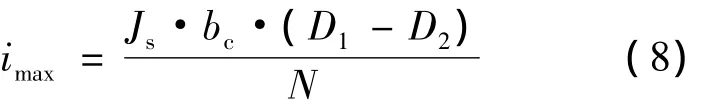
由于气隙磁密B受D1、D2影响较大，在利用式(9)进行计算时，应合理预计该值，并根据工作环境选取恰当的电流密度。

1.3算例

某样机主要指标和参数选取如表1所示。

式中:Js——线圈允许承受的电流密度。

由式(1)～(8)，得到斯特林制冷机用直线电机的主要尺寸估算公式:

表1 样机指标和参数选取

则根据式(9)可得:

可根据实际情况选取合适的bc、D1、D2，该算例中取为:bc=13×10-3m，D1=54.5×10-3m，D2=43×10-3m。

2 动磁式直线电机有限元分析

采用磁路法只能对斯特林制冷机用直线电机的参数进行粗略估算，难以准确计算。一般情况下，电机的磁场分布并不均匀，端部漏磁较大，同时，动子位置的变化加剧了漏磁情况的复杂程度。为准确计算电机的电磁参数，应进行磁场分析，目前最常用的磁场数值分析法是有限元法。在电机设计时，一般首先采用磁路法估算电机主要尺寸，再利用有限元法进行优化和精确计算，可以节约计算时间，加快设计速度。

利用该类直线电机具有的轴对称性，采用柱坐标系下的轴对称场建立平面求解模型，可以在不建立三维模型的情况下对电机参数进行计算，计算结果包含了电机的端部效应。基于麦克斯韦方程组的基本原理，引入矢量磁位A，在柱坐标系下电机磁场可表示为

式中:μ——材料磁导率;

J0——绕组电流密度;

Jm——永磁体等效磁化电流密度;

Ht——磁场强度的切向分量;

s1，s2——第一类、第二类边界条件。

Maxwell是基于上述原理的电机电磁场分析专用软件。图2是利用该软件建立的前述算例的平面几何模型，采用rz坐标系，z轴为对称轴。该算例样机与图1所示样机结构略有不同。图1所示电机动子采用双磁钢、径向充磁，图2所示电机动子采用单磁钢、轴向充磁，两种结构电机工作原理和分析方法均相同。图3所示为动子位于中心位置时的磁力线分布情况。从图3中可以看出电机端部及线圈之间的极间均存在漏磁。该漏磁随D1、D2的变化及动子位置的变化而变化，仿真显示D1、D2差别越大、动子越靠近行程的两个端部极限位置时，漏磁越大。

图2 样机几何模型

图3 磁力线分布

为分析有效气隙内(包括实际气隙和线圈部分)的径向磁密分布情况，在图2所示的不同位置画出3条直线，图4所示为沿对应直线的径向磁密分布情况。从图4中可以看出，径向气隙磁密随位置而变化，半径越大的位置气隙磁密越小，这说明半径越大时漏磁越大。在磁路法计算选取B值时，可以根据预估的尺寸建立简单的几何模型，然后用有限元法对该值进行校正，避免实际值与预估值有太大偏差。

3 比推力测试方法及结果对比

图4 不同位置的径向气隙磁密分布

比推力是斯特林制冷机用直线电机的一项重要测试内容，根据定义，比推力为单位电流产生的轴向推力。由于电机的端部效应不可避免，电机动子不同位置时其比推力会有所不同。在保持电机绕组电流不变的情况下，分别测量不同位置的电机推力，可以得到比推力-位移曲线。本文提出一种将直线电机竖直放置的测试方法，测试设备和工装夹具都很简单，操作方便。所采用的测试设备主要包括电源、弹簧拉压试验机(TLSS200型)等。

在测试之前，利用非磁性的工装夹具将电机的定子和动子组装固定，定子和动子之间利用线性轴承和心轴支撑，两者之间的摩擦力很小，可以忽略。具体测试步骤如下:

(1)将电机水平放置，使电机动子处于自由状态。在自定位力的作用下，动子会停留在一个平衡位置，将该位置作标记。

(2)将电机垂直放置在试验机托盘上，由于重力作用，动子会低于所标记的平衡位置。调节绕组电流，使动子恢复平衡位置，记录该电流值i1，然后调节试验机压板，使压板和电机心轴顶端处于临界接触状态，并将数显位置和力分别清零。

(3)维持电流i1不变，调节试验机压板的位置，记录n个不同位置的推力Fk(i1)，k=1，2，…，n。

(4)增加电流至i2，重复步骤3，记录不同位置推力Fk(i2)，k=1，2，…，n。

则电机的比推力可用式(11)计算:

该算法可以将外界因素(如板簧、摩擦力、重力等)的影响消除，但是得到的比推力仅指纯电磁力，并不包含自定位力。当考虑自定位力时，可通过弹簧拉压试验机的拉力测量模式得到动子不同位置的定位力fk(i=0)(该力应为扣除重力作用后的数值)。则式(11)变为

利用Maxwell软件对一台样机进行了有限元仿真计算，利用所设计的测试装置对样机进行了比推力测试，测试结果如表2所示。从对比结果可以看出，计算结果与测试结果吻合的很好，说明本文给出的仿真方法和测试方法是合理可行的，可用于该类电机的设计和测试。

表2 样机仿真结果和测试结果对比

4 结语

本文分析了斯特林制冷机用直线电机的结构特点，给出了电机主要尺寸估算方法，利用该方法对一台样机进行了估算。基于Mexwell磁场分析软件建立了该样机的有限元模型，并对性能参数进行仿真计算。最后，采用本文分析的一种结构简单、易于操作的测试方法对样机比推力进行测试，并将测试结果与计算结果进行对比，两者之间十分吻合，验证了计算方法和测试方法的有效性和准确性。

［1］闫春杰，潘雁频，许国太，等.80 K/0.8 W星载斯特林制冷机研制［J］.真空与低温，2007(4):237-239.

［2］陈楠，唐亚杰，徐烈，等.线性压缩机用动磁式直线电动机［J］.上海交通大学学报，2007(3):473-478.

［3］郑文鹏，陆英，张洲，等.斯特林制冷机用直线电机机构及特点分析［C］∥第十四届中国小电机技术研讨会论文集，2009:100-104.

［4］邰晓亮.动磁式直线电机驱动微小型活塞压缩机理论分析及实验研究［D］.上海:上海交通大学，2009.

［5］丁国忠，张晓青，何明顺，等.斯特林用直线压缩机的研究［J］.低温技术，2008(6):458-462.