基于混合励磁电机的直驱式风电系统

叶斌英，阮 毅， 杨 勇，汤燕燕

(上海大学机电工程与自动化学院，上海 200072)

0 引言

随着人们环境意识的加强，风力发电凭借其高效、环保、大功率的优势得到了越来越广泛的关注［1-4］。典型的风力发电技术分为恒速恒频和变速恒频两种。恒速恒频风电系统通常将发电机与电网直接连接;变速恒频风电系统一般利用电力电子装置对发电机进行控制，与恒速恒频发电技术相比，其具有显著的优越性，大大提高了风能转换效率，逐渐成为主流。变速恒频风力发电并网技术主要分为双馈式和直驱式两种。双馈式风力发电系统需要齿轮箱升速，维护费用高，而采用多极同步电机的直驱式风力发电系统结合电力电子装置，发电机可以在低速下发电运行，省去了齿轮箱，该系统已成为近年的研究热点［5-9］。

最大风能跟踪是风力发电的基本问题。在一定的风速下，存在一个最佳的发电机转速使得系统捕获的风能最大。对于直驱式风力发电系统，文献［10］分析了典型的基于永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)的矢量控制并网系统结构和最大风能跟踪方法，利用可控的整流桥、逆变桥分别控制机侧以获取最大风能和网侧并网逆变，通过直流母线进行联系，可以实现并网逆变和最大风能跟踪的目的，但存在着需要两套大功率变流器的缺点。文献［11］提出了不添加整流桥实现最大风能跟踪的控制方法，使系统更加稳定，但是控制方法复杂。文献［12］和文献［13］各自提出了在直流母线上添加BOOST电路进行最大风能跟踪的方法，拥有良好的跟踪性能，但是BOOST电路限制了系统的功率。由于永磁电机本身励磁不可控，为了达到捕获最大风能的目的，上面提到的这些基于PMSM的最大风能跟踪方法都需要在主电路上添加电力电子装置，辅助实现最大风能跟踪。近年，广受各国学者关注的混合励磁同步电机［14-16］(Hybird Excitation Synchronous Motor，HESM)在永磁体励磁的基础上添加了电励磁，同时具有电励磁同步电机和PMSM优点，在变速或负载不稳定的发电场合通过调节励磁电流即可提供恒压电源。如果在直驱式风力发电系统中，利用 HESM替代PMSM，通过混合励磁电机的电励磁协调控制直流母线电压，可省去一部分大功率电力电子装置，同时达到最大风能跟踪的目的。

本文推导了HESM和并网逆变器的数学模型，并在此基础上给出了本文所采用的系统结构模型，以及相应的最大风能跟踪策略，最后通过仿真验证了该系统结构的正确性。

1 数学模型

1.1 HESM数学模型

本文介绍的风力发电并网系统采用的HESM结构如图1所示:装在定子上的直流励磁线圈首先在旋转的转子上感应出交流励磁电流，该交流电又经过转子上的整流器得到直流电，该直流电与装在转子上的永磁体一起产生励磁作用，再安装在定子上的主绕组中感应出电动势。

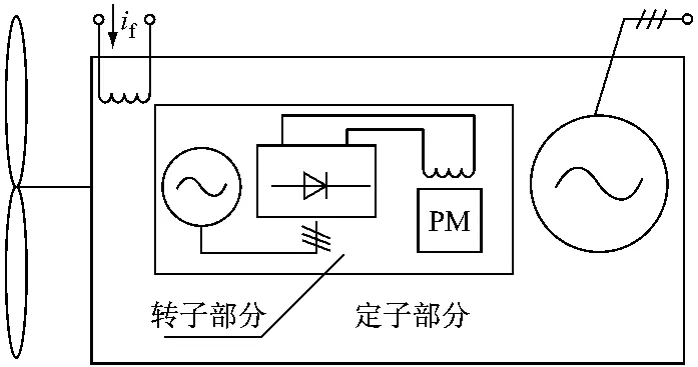
图1 HESM内部结构示意图

虽然HESM结构比较特殊，但从电磁关系的角度来看，HESM与普通PMSM相比，仅多了一个可以调节电流的励磁绕组。因此，仍然可以采用dq坐标系来分析HESM。由于定子坐标系下的HESM方程式是一组与转子瞬时位置有关的非线性微分方程式，只能采用与转子同步转速旋转的dq坐标轴系统的变换来消除微分方程中的这种非线性关系。取由定子绕组端点流入电机中心点方向作为定子各相电流的参考正方向，绕组磁链Ψ和电流i的正方向符合右手螺旋法则，永磁体产生的主极磁通方向取为d轴的正方向，q轴超前d轴正方向90°电角度。由此可得到电枢绕组和励磁绕组的磁链方程式为

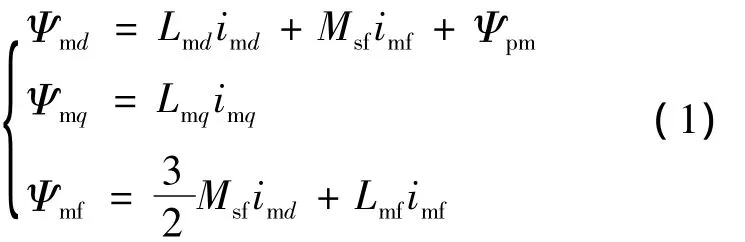
式中:Lmd，Lmq——直轴和交轴电感;

Msf——励磁绕组与电枢绕组互感的幅值;

Lmf——励磁绕组自感;

Ψpm——永磁体匝链电枢绕组的磁链幅值。

根据电压方程，经推导得电流微分方程为

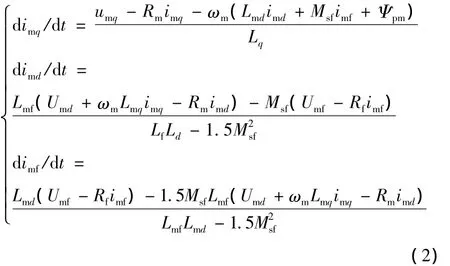
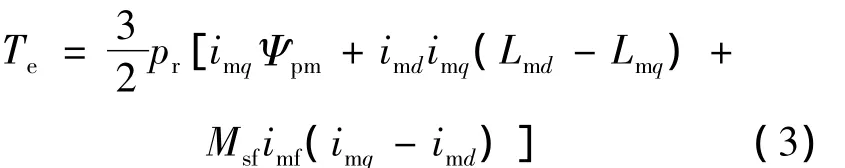
式中:pr——电机转子极对数;

ωm——转子的电角速度;

Rm——定子绕组阻值;

Rf——励磁绕组阻值。

1.2 三相并网逆变器的数学模型

三相并网逆变器作为发电系统与电网连接的桥梁，在整个系统中至关重要。三相电压型并网逆变器一般采用电网电压定向的矢量控制策略［18-19］，其拓扑结构如图 2 所示。其中:iA、iB、iC为并网逆变器输出电流;uA、uB、uC为并网逆变器

电磁转矩方程为:输出电压;eA、eB、eC分别为三相电网电压;L、R为连接并网逆变器与电网的电感和电阻;C为母线上的电容。各量的参考方向如图2所示。

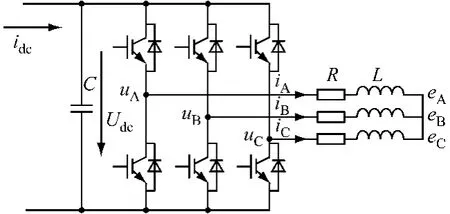
图2 三相电压型的并网逆变器

设三相电网电压为

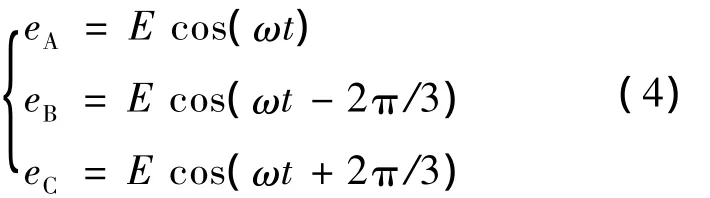
式中:E——相电压的峰值;

ω——电网角频率。

同步旋转坐标系中，将d轴定在电网电压的合成矢量上，通过检测电网电压的空间角度，可以得到脉宽调制(Pulse Width Modulation，PWM)整流器三相旋转坐标系dq轴的数学模型［17］:

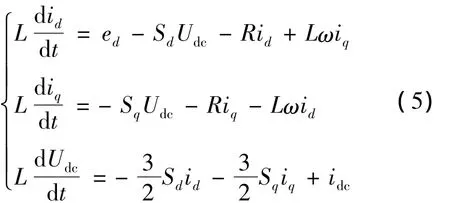
式中:Sd、Sq——开关函数在dq坐标系中的表示;

ed——电网电压的d轴分量;

id、iq——电流的d、q轴分量;

ω——电网电压角频率。

逆变输出的功率为

2 控制策略

2.1 风机特性

根据贝兹(Betz)理论，风轮机实际得到的功率与风速的三次方有关。在风速ν下运行时，单位时间内捕获的风能为

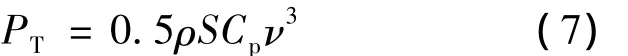
式中:ρ——空气密度;

S——风轮的扫掠面积;

Cp——风能利用系数，反映风轮机利用风能的效率，是叶尖速比λ和叶片节距角Q的函数。

叶尖速比:

式中:ωT——风轮旋转机械角速度;

R——风轮叶片半径。

变速恒频机组正常运行时，叶片节距角Q固定。因此，Cp的大小主要决定于λ。

一定风速下典型的风轮机的Cp-λ曲线如图3所示，而不同风速和转速下的功率曲线如图4所示。由图3可知，对于一个特定的风速ν，总存在一个最佳的叶尖速比λopt，对应着一个最大的风能转换系数Cpmax。从图4可以看出，在同一个风速下，不同的转速会使风力机输出不同的功率。只要能够根据风速的变化，适当调整风力机转速，使λ始终为λopt，即可使风力机运行在最佳功率点上，获得最大风能转换效率。

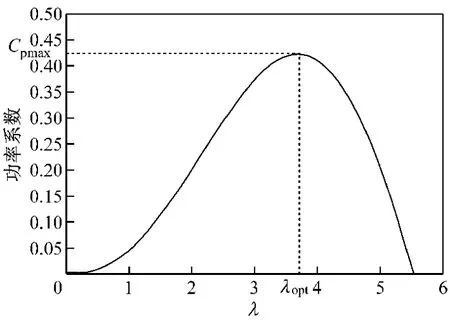
图3 风机的效率特性

图4 不同风速和转速下功率特性

2.2 控制策略

本文采用的基于HESM的直驱式风力发电系统模型如图5所示。系统采用了交-直-交结构，风轮机带动连轴的HESM，电机端子感应出频率和幅值都不固定的交流电，该交流电首先通过不可控整流桥得到直流电，再通过并网逆变器逆变为频率固定(50 Hz)的三相电输送到电网上。系统不仅能够根据风能的大小逆变有功功率至电网，还能根据需要逆变无功功率至电网。

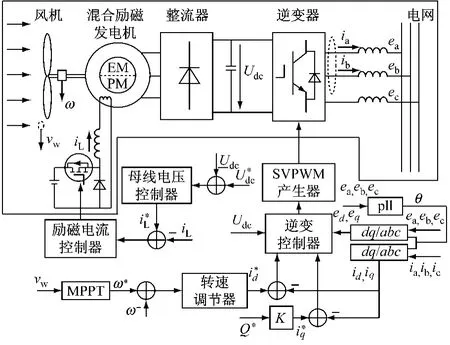
图5 基于混合励磁电机的直驱式并网发电系统结构图

根据图4所示的风轮机功率特性，每一风速下的最佳叶尖速比λopt是已知的。依据实际风速，调节发电机转速维持实际的λ=λopt，便可获得最大风能。

对于由风机和混合励磁电机组成的连轴系统而言，其运动方程如下:

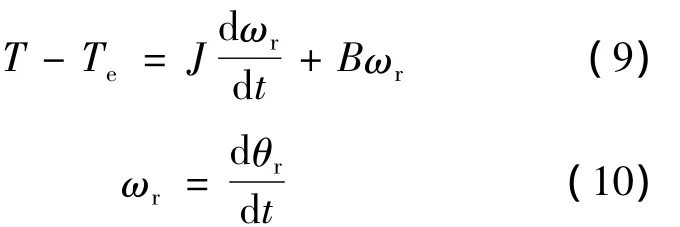
式中:T——风机输出转矩;

Te——混合励磁电机的电磁转矩;

J——系统转动惯量;

B——系统摩擦系数;

ωr——转子机械角速度。

从式(9)、(10)可以看出要控制发电机的当前转速只要控制发电机的电磁转矩，又根据式(3)，电磁转矩受到发电机输出电流即输出有功功率影响。因此，只要控制电机输出的电流大小，即可控制发电机的转速。结合式(2)和图5实线框内所示的主电路拓扑结构，假设直流母线上的电压恒定，发电机流出的电流受到逆变器输出电流的唯一控制。本文通过调节混合励磁电机的电励磁电流大小协调控制直流母线电压为一恒值，这样发电机的转速可通过逆变电流大小进行控制。母线电压的恒定也保证了并网逆变输出电流波形的质量，以此来达到并网逆变和最大风能跟踪的目的。

图6为母线电压控制环的结构，母线电压的差值经过PI作为混合励磁电机的电励磁给定，又通过PI得到BUCK电路开关控制信号。鉴于混合励磁电机的结构，两个PI调节器的输出限幅都只能是正值。图7为并网逆变电流控制环的结构，根据当前的风速可以得到唯一的最佳电机转速，此转速经过PI调节器得到有功电流的给定信号，与无功电流的给定信号一起得到空间矢量脉宽调制(SVPWM)模块的参考信号。风机的转速可以快速地根据风速的变化而变化，使得系统波动小、反应快。

图6 直流母线电压控制器

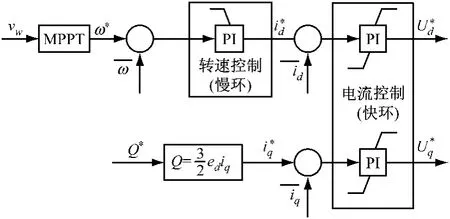
图7 转速控制器

3 仿真结果

为验证上述最大风能跟踪算法的正确性，在MATLAB/Simulink下搭建了系统进行仿真。仿真时采用的发电机参数如表1所示。

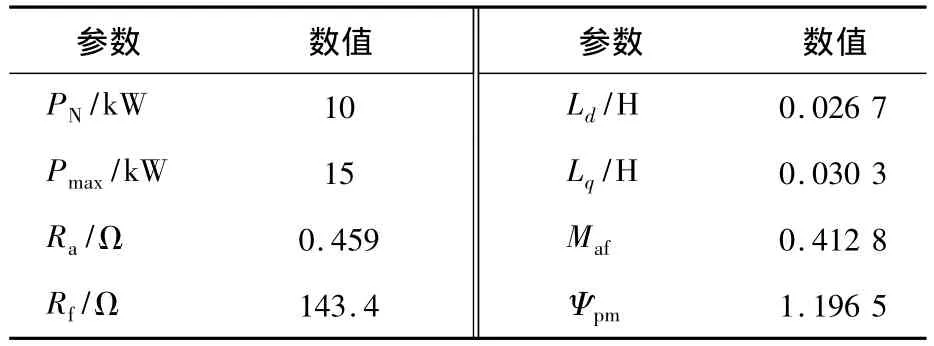
表1 仿真用混合励磁机参数

模拟的风速0 s时突给11 m/s，2 s时逐渐变化至13 m/s，在3.5 s时逐渐升至15 m/s，5.5 s时逐渐降至14 m/s，观察风机转速、逆变电流、母线电压的变化过程。

从图8和图9可以看出发电机的转速可以快速跟随风速变化。图10反映了发电机转速变化以后，直流母线电压能够维持在给定的600 V。图11是7.5～7.6 s之间a相的逆变电压缩小40倍的波形和 a相的电流波形，此时控制无功输出为0。从图11可看出电流和电压同相位。图12反映出风速变化后风机捕获的风能大小也跟随风速变化。图13是d轴电流给定的随风速变化的波形。

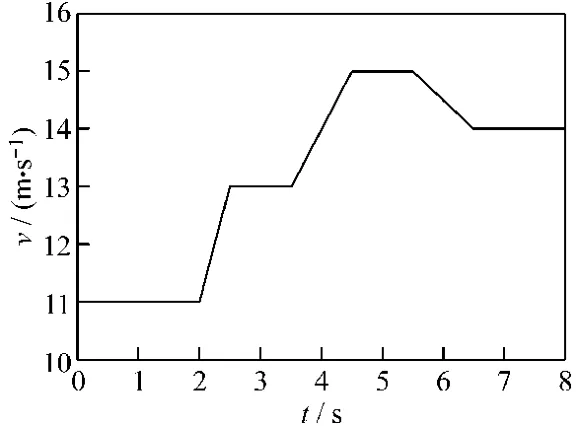
图8 风速变化仿真波形

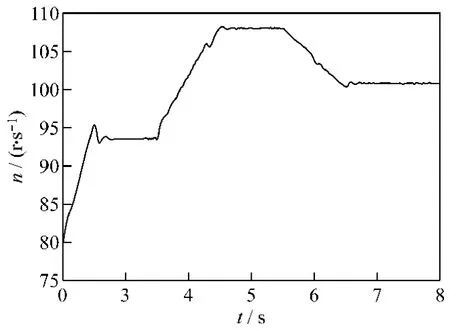
图9 发电机转速仿真波形

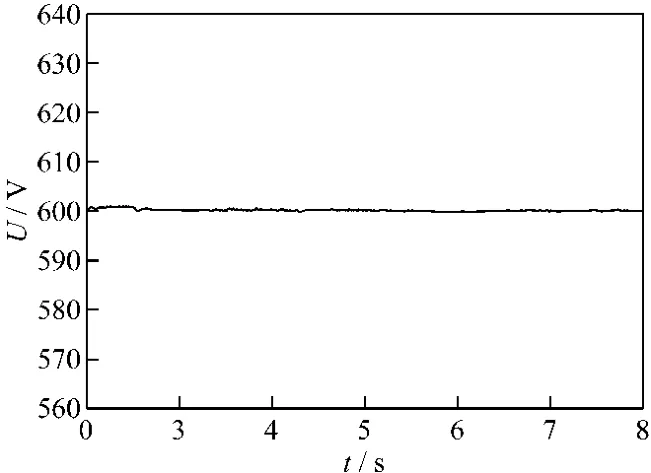
图10 直流母线电压

图11 a相逆变电压电流波形(无功给定为0)

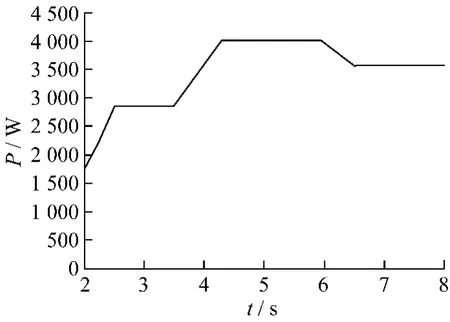
图12 风机输入功率

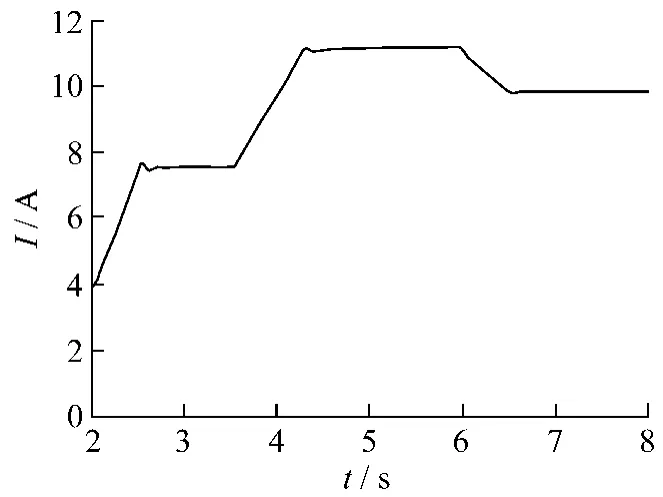
图13d轴(有功)电流变化(无功给定始终为0)

4 结语

本文介绍了一种基于HESM的直驱式风力发电系统结构，推导了相应的数学模型，并在此基础上提出了最大风能跟踪控制方法。该系统结构简单、控制方法清晰，通过混合励磁电机的电励磁环节可以省去部分大功率电力电子器件，而且风能跟踪的实时性高，并网逆变输出的电流波形质量好。

［1］Tapia G，Tapia A.Wind generation optimization al-gorithm for a doubly fed induction generator［C］∥IEE Proceedings，Generation，Transmission and Distribution，2005，152(2):253-263.

［2］Tapia A，Tapia G，Ostolaza J X，et al.Modeling and control of a wind turbine driven doubly fed induction generator［J］.IEEE Transactions on Energy Conversion，2003，18(2):194-204.

［3］李晶，王伟胜，宋家骅.变速恒频风力发电机组建模与仿真［J］.电网技术，2003，27(9):14-17.

［4］苑国锋，柴建云，李永东.变速恒频风力发电机组励磁变频器的研究［J］.中国电机工程学报，2005，25(8):90-94.

［5］Carrasco J M，Franquelo L G，Bialasiewicz J T，et al.Power electronic systems for the grid integration of renewable energy sources:a survey［J］.IEEE Transactions on Industrial Electronics，2006，53(4):1002-1016.

［6］Rajib Datta，V T Ranganathan.A method of tracking the peak power points for a variable speed wind energy conversion system［J］.IEEE Trans Energy Conversion，2003，18(1):163-168.

［7］Eftichios Koutroulis，Kostas Kalaitzakis.Design of a maximum power tracking system for wind-energy-conversion applications［J］.IEEE Trans Ind Electron，2006，53(2):486-494.

［8］Y Higuchi，N Yamamura，M Ishida，et al.An improvement of performance for small-scaled wind power generating system with permanent magnet type synchronous generator［C］∥IEEE Industrial Electronics Society Conference，2000(2):1037-1043.

［9］徐大平，张新房.风力发电控制问题综述［J］.中国电力，2005，38(4):70-74.

［10］Li Shu Hui，Haskew T A.Characteristic study of vector-controlled direct driven permanent magnet synchronous generator in wind power generation［C］∥Power Engineering Society General Meeting，2008(20-24):1-9.

［11］Srighakollapu N，Sensarma P S.Sensorless maximum power point tracking control in wind energy generation using permanent magnet synchronous generator［C］∥Industrial Electronics 34th Annual Conference of IEEE，10-13:2225-2230.

［12］Esmaili R，Xu L，Nichols D K.A new control method of permanent magnet generator for maximum power tracking in wind turbine application［C］∥Power Engineering Society General Meeting，San Francisco，California，USA，2005(3):2090-2095.

［13］Chen Yi Guang，Wang Zhi Qiang.A control strategy of direct driven permanent magnet synchronous generator for maximum power point tracking in wind turbine application［C］∥International Conference on Electrical Machines and Systems，2008:3921-3926.

［14］Tapia J A，Leonardi F，Lipo T A.Consequent-pole permanent magnet machine with field weakening capability［J］.IEEE Transactions on Industry Applications，2003，39(1):1704-1709.

［15］Zhang Hong Jie，Tang Ren Yuan.Theory and design of hybrid excitation permanent magnet synchronous generators［C］∥International Conf on Electrical Machines and System，Shenyang，2001(2):898-900.

［16］Wu R，Dewan S B，Slemon G R.Analysis of an AC-to-DC voltage source converter using PWM with phase and amplitude control［J］.IEEE Transactions on Power Electronics，1991，27(2):355-364.

［17］Noguchi T，Tomiki H，Kondo，et al.Direct power control of PWM converter without power-source voltage sensors［J］IEEE Transactions on Industrial Application，1998，34(3):473-479.

［18］Malinowski M，Jasinski M，Kazmierkowski M P.Simple direct power control of three-phase PWM rectifier using space-vector modulation(DPC-SVM)［J］.IEEE Transactions on Industrial Electronics，2004，51(2):447-454.

［19］Kazmierkowski M P，Malesani L.Current control techniques for three-phase voltage-source PWM converters:a survey［J］.IEEE Transactions on Industrial Electronics，1998，45(5):691-703.