灰色微分方程的参数改进

付晶园，罗明奇，马少仙

（西北民族大学 计算机科学与信息工程学院，甘肃 兰州730030）

灰色微分方程的参数改进

付晶园，罗明奇，马少仙

（西北民族大学 计算机科学与信息工程学院，甘肃 兰州730030）

分析了在求解微分方程（1）时由于给定的定解条件的不合理性，结合灰色系统理论和多元统计分析的原理，提出使用拟合原始数据的曲线方程近似代替微分方程求解中的参数常数c，使得预测方程得到一定的改进.

微分方程；参数；预测

灰色系统（Grey System）理论是八十年代发展起来的一门新学科.自从1982年我国学者邓聚龙教授创立灰色系统理论（Gray Theory）以来，灰色系统理论已经广泛的应用于各个学科中.艾什比（Ashby）将内部信息未知的对象称为黑箱（Black Box），这种称谓已被人们普遍接受.这里用“黑”表示信息未知，用“白”表示信息完全明确，用“灰”表示部分信息明确，部分信息不明确.相应的，信息完全明确的系统称为白色系统，信息未知的系统称为黑色系统，部分信息明确，部分信息不明确的系统称为灰色系统.

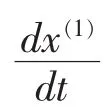
1 相关理论

依据灰色系统理论［1］，GM（1，1）模型的具体算法如下：

生成序列X（1）相应的微分方程为：

B中背景值Z（1）为X（1）的紧邻均值生成序列：Z（1）=（z（1）（2），z（1）（3），…，z（1）（n）），其中，z（1）（k）= 0.5（x（1）（k）+x（1）（k-1）），k=2，3，…，n.

在求解微分方程（1）时，得出通解为：

将其离散化，得到：

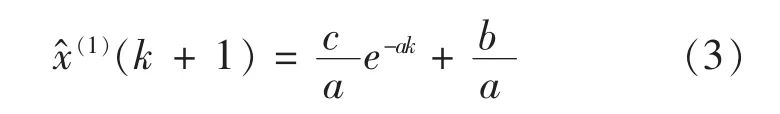
为了求解常数c，需要一个定解条件，在GM（1，1）中，令（1）=x（1）（1）=x（0）（1），则有：

（4）即为GM（1，1）的预测方程，此时可利用一次累减（1-IAGO）得到还原序列：

2 主要结论

由相关理论可知，在求解微分方程（1）时，得到（2），将其离散化得到（3），为了求解常数c，需要一个定解条件，在 GM（1，1）中，令（1）=x（1）（1）= x（0）（1），得到预测公式（4），由给定的初值条件可知，拟合曲线在坐标平面（k，x（1）（k））必然经过点（1，x（1）（1）），而由最小二乘法原理，拟合曲线不一定通过第一个数据点，但是其必定与第一个建模的数据点具有一定的差距，于是，将（1）=x（1）（1）作为已知条件的理论根据并不存在，另外，考虑到x（1）（1）是一个很旧的数据，与未来的关系不密切，而且不是通过累加生成得到的，规律性不强，更不符合灰色系统理论的信息原则.同时由于定解条件给定的不唯一性，使得无法确定一个精确度相对较高的预测方程，基于此，对于GM（1，1）模型的改进方式有很多种，谭冠军的GM（1，1）模型的背景值构修正［2-4］；孙辰军，王翠茹的GM（1，1）模型的残差修正［5］；王忠桃，彭鑫的初值修正的灰色预测模型的改进［6］.

通过对微分方程（1）的求解中，得到了通解（2），在通解（2）的求解中不再引入初值条件，不再化为定解问题，而是根据多元统计分析的思想，并结合灰色关联度的性质，在其中引入曲线拟合，即：根据灰色系统模型理论建立预测方程（1），得到其通解（2），关于（2）中的参数c，由经济学原理知道，当年的经济数据总是和前一年的经济数据具有一定的关系，所以根据已知的数据依据多元统计分析的原理，建立曲线拟合方程f（t），其必然是关于前一年经济数学函数关系，并将此拟合曲线方程作为参数c的取值，由此通过（2）进行预测研究.

据此得出：

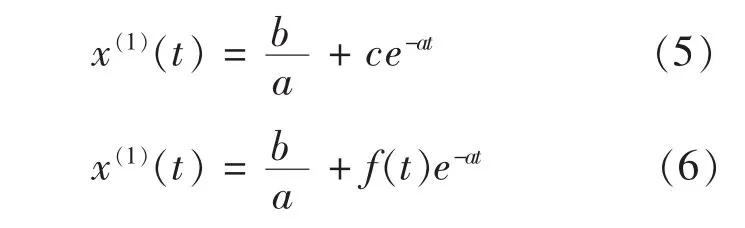
其中f（t）是根据已知数据所进行曲线拟合方程.于是，在原始数据序列满足准指数和光滑性的前提下可以据此来进行预测研究.

［1］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2005.

［2］谭冠军.GM（1，1）模型的背景值构造方法和应用（Ⅰ）[J].系统工程理论与实践，2000（4）：98-103.

［3］谭冠军.GM（1，1）模型的背景值构造方法和应用（Ⅱ）[J].系统工程理论与实践，2000（5）：125-132.

［4］谭冠军.GM（1，1）模型的背景值构造方法和应用（Ⅲ）[J].系统工程理论与实践，2000（6）：70-74.

［5］孙辰军，王翠茹.残差灰色预测模型的改进与应用[J].统计与决策，2005（3）：19-20.

［6］王忠桃，彭鑫.基于初值修正的灰色预测模型的改进及其应用[J].重庆工学院学报，2007（10）：81-84.

［7］张大海，江世芳，史开泉，等.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002（8）：140-142.

［8］罗荣桂，陈炜.灰色模型的一点改进及应用[J].系统工程理论与实践，1988（4）：46-52.

责任编辑：毕和平

IMprovement of Parameters of the Gray Differential Equation

FU Jingyuan，LUO Mingqi，MA Shaoxian
（College of Computer Science and Information Engineering，Northwest University for Nationalities，Lanzhou 730030，China）

The unreasonabilty in solving grey differential equations（1）on the basis of the given boundary conditions was analyzed.Combined with the ray systeMtheory and the principle of multivariate statistical analysis，the curve equation approximation instead of parameters constant in solving differential equations was proposed，which also improve the forecast accuracy.

differential equation；parameter；forecast

O 175

A

1674-4942（2010）02-0123-02

2010-02-20