例谈求解不等式中的放缩技巧

●江厚利 (杭州市第二中学 浙江杭州 310053)

不等式问题是竞赛中的热点问题，用放缩法解不等式问题对考生来说也是一个难点，难就难在放缩时需要综合运用一些技巧.譬如，添项舍项、换元转化、以直代曲、借助重要不等式等.同时，还要把握好放缩的方向与度，即要放缩得恰到好处.本文结合实例，谈谈不等式证明中的放缩技巧.

1 利用函数的单调性放缩

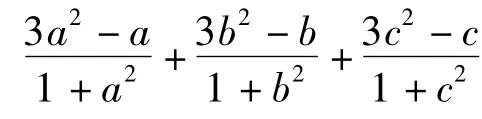
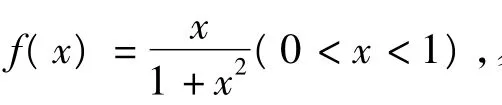
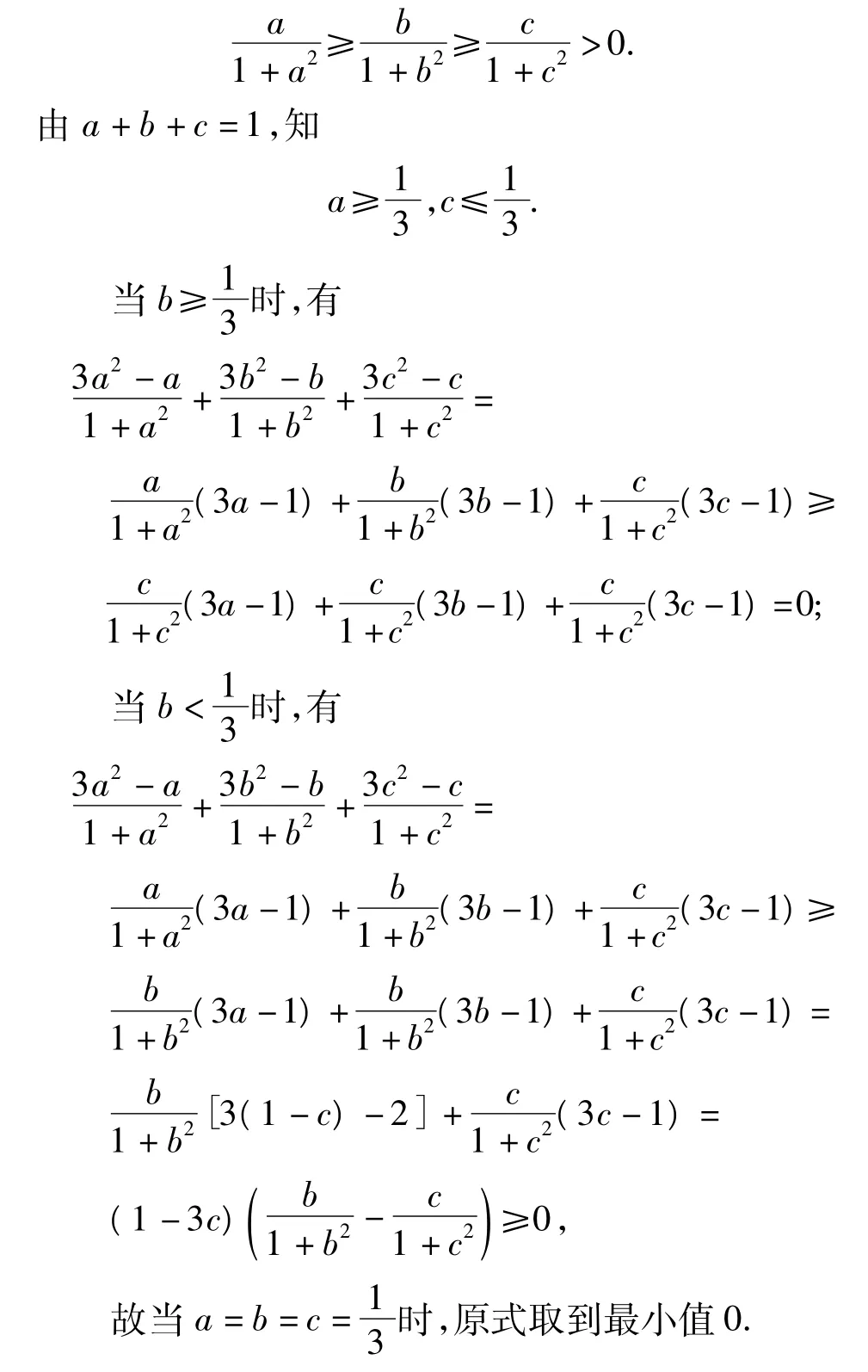
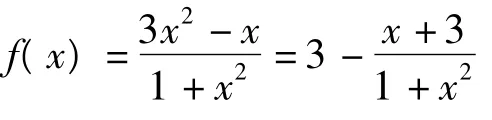
2 利用重要不等式放缩

上式等号成立的充要条件是

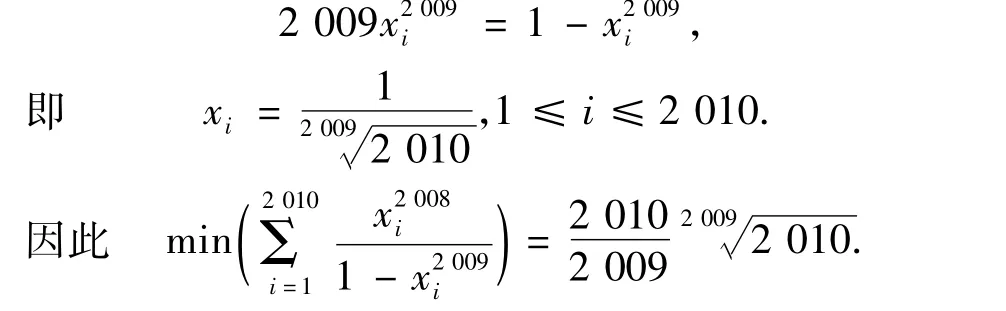
3 利用添项、舍项放缩

例3 已知数列{an}的前n项和Sn满足Sn=2an+(-1)n，n∈N+，证明：对任意整数 m ＞4，有

分析利用已知条件中的an与Sn的关系，易求得

由于待证不等式的左边比较复杂，因此先要设法将左边的项放缩，使之能够求和.

(1)当m＞4且m为偶数时，

(2)当m＞4且m为奇数时，

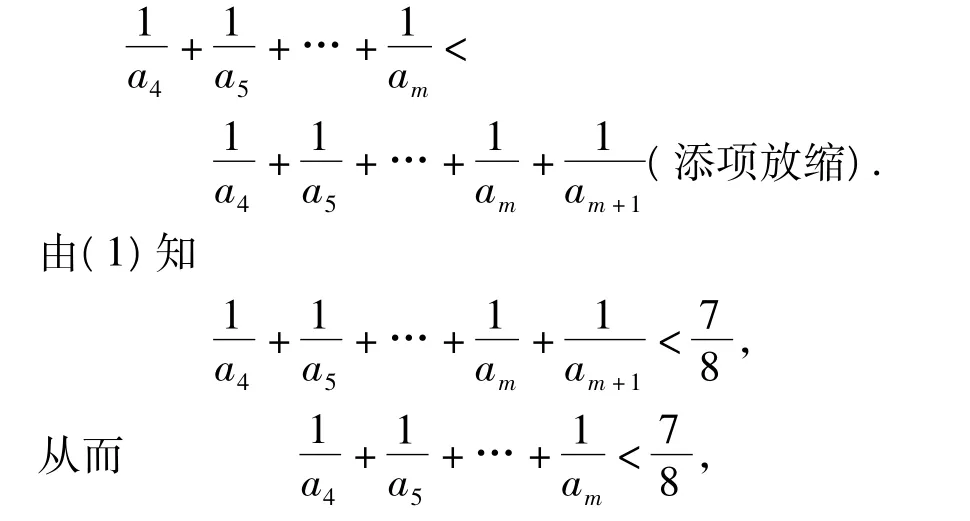
综合(1)，(2)可知，结论成立.

评注当-1和1在待证和式的项中交错出现时，仅考虑通项放缩往往不能奏效.若本题将通项中的-1和1舍去，则虽然可以化为等比数列求和，但由于通项有的放大，有的缩小，仍不能确定和式是放大还是缩小.此时，可以把奇偶相邻项捆绑求和后再放缩.注意在添项、舍项放缩时，不能放缩过头.

4 利用曲线的切线放缩

例4 设实数a，b，c满足a+b+c=3，求证：

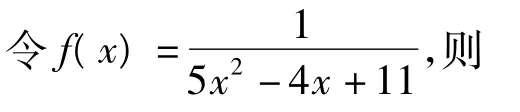
当且仅当a=b=c=1时，等号成立.

评注本题蕴含了一个非常朴素且重要的数学思想方法——以“直”代“曲”：将函数的曲线图像转化为相应的切线，以简化表达式.这也是一种放缩!对于当且仅当各变元相等时不等式取得等号的一类不等式，是一种常用且有效的证明方法.

5 利用积分思想放缩

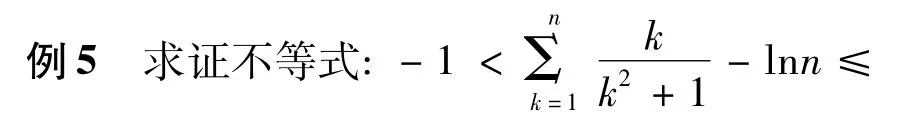
(2009年全国高中数学联赛加试试题)

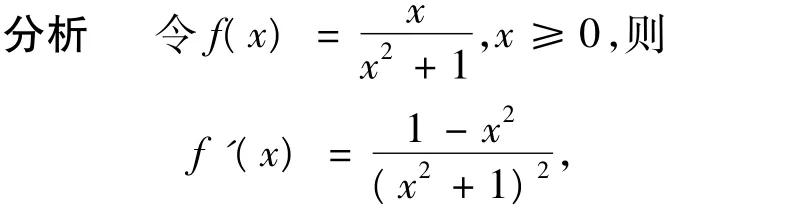
故f(x)在［0，1］上单调递增，在［1，+∞)上单调递减.结合函数图像可得，对任意k∈N+，有

评注分割及“曲直”替换是积分的基本思想方法.本题求解的关键是逆用积分的思想，通过直线转化为曲线，将不等式转化为某个函数的上和或下和，并结合积分中的上和不小于积分值、下和不大于积分值的原理即可以达到证题目标.