高职数学建模与数学实验教学反思*

王积建 韩义秀

（浙江工贸职业技术学院 a.基础部；b.汽车与机电工程系，浙江 温州 325003）

高职数学建模与数学实验教学反思*

王积建a韩义秀b

（浙江工贸职业技术学院 a.基础部；b.汽车与机电工程系，浙江 温州 325003）

目前《数学建模》与《数学实验》教学存在3个误区：（1）内容重复；（2）分科教学；（3）“高效灌输”的授受式教学. 将《数学建模》和《数学实验》两门课程进行整合，才有望解决以上突出问题.。

数学建模；数学实验；课程整合；教学反思

1 问题提出

截至2008年，全国大学生数学建模竞赛已经举办了17届，参赛校数遍及全国31个省、市、自治区（包括香港），从1992年的79所增加到2008年的1023所；参赛队数从1992年的314队增加到2008年的12846队（其中本科组10384队，专科组2462队）；参赛学生累计达到23万之多[1]。截至2008年，我国共有高职高专院校1168所，在校生近880万人，占全日制普通高校本专科在校生的47%[2]，高职教育已成为我国高等教育的“半壁江山”，而数学建模竞赛也已成为全国高校（包括高职院校）规模最大的课外科技活动。

然而，职业技术学院近两年开始推行“工学结合”培养模式，理论课程的学习一般压缩为2年，高等数学只开64课时左右，经济数学只开36课时左右，有些专业干脆砍掉了数学课程，这就明显减少了开展数学建模学习的课时。近两年受数学建模竞赛效应的影响数学建模选课还出现新情况，很多学生由于专业课程的需要（比如计算机软件专业、自动控制专业等），或者撰写毕业论文的需要（比如市场营销专业），也渴望学习和掌握与数学建模有关的知识。我校数学建模协会每学年招收新学员时都会出现爆满的场面，就说明了这个问题。

为了应对广大学生对数学建模学习和竞赛的渴求，许多院校都在学生业余时间进行培训。由于学生课外时间有限，所以仅靠延长课时的方式已经不能满足学生的需求。另一方面，延长课时的必然结果是学生的课业负担加重，学生出现厌学情绪。 总之，学生对数学建模知识技能的需求与学生业余时间的有限成为当前数学建模教学的突出矛盾。

基于以上分析，如何实施数学建模和数学实验课程，以满足广大学生对数学建模知识和能力的日益增长的需求，是需要亟待研究的新问题。

2 当前数学建模和数学实验的教学体系

通过考察某些高职院校中的数学实验和数学建模课程，可以发现基本形成了符合高职学生需求的内容体系。

2.1 高职数学建模教学体系

主要有：

数学建模简介。包括：数学模型与数学建模、大学生数学建模竞赛简介、数学建模论文的撰写方法。

初等模型。包括：代数模型（涵盖函数、方程、不等式、数列、三角等）、几何模型、平面解析几何模型、向量模型、简易逻辑模型等。

数学建模专题训练。包括：线性规划、目标规划、非线性规划、动态规划、网络规划、微积分和微分方程模型、随机模型、插值与拟合、决策模型（含层次分析法）等。

数学建模综合训练。包括实例问题解决、历届竞赛优秀论文等。

2.2 高职数学实验教学体系

数学实验课程主要以MATLAB软件为主，以LINDO、LINGO等软件为辅，实验内容主要有：

MATLAB 入门、微积分实验、线性代数实验、概率统计实验、线性规划实验、整数规划实验、0-1规划实验、二次规划实验、非线性规划实验、解方程和解非线性方程组实验、多元函数微积分实验、微分方程（组）实验、投入产出实验、数据插值实验、数据拟合实验、线性回归实验等。

从数学建模和数学实验课程的内容体系来看，大多数内容是对应设置的，这是由数学建模的性质决定的。因为从问题解决的全过程来看，数学模型建立起来以后，紧接着就是数学实验环节了，也就是在数学实验平台上对模型进行求解和验证，如果求解的结果与实际不符的话，还需要进一步分析和探究，并改进模型。这种课程设置模式不妨称之为“并联式”，如图 1所示。

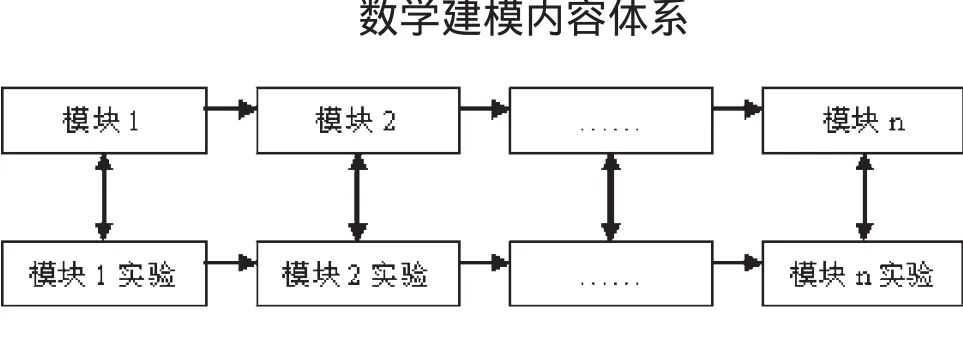
图 1 “并联式”课程设置模式

3 教学反思

通过对目前高职数学建模与数学实验课程教学体系进行反思，存在着以下四个方面的误区。

误区一：内容重复。从2.1节和2.2节可以看出，数学建模专题部分和数学实验部分几乎是对应设置的。事实上，无论是结构良好问题，还是结构不良问题[3]，其解决是一个完整的过程，只不过分为两个阶段解决的，一个是建模阶段，一个是求解、分析和改进阶段，但是把一个整体性的过程无端地分割成两个相对独立的过程，造成了知识的割裂和教学效率的低下。

成因：首先，从问题解决的全过程的内在逻辑来看，当数学模型建立起来以后，紧接着就是数学实验环节了，这就需要数学建模必须要有对应的数学实验技术相配套；其次，从师资力量上来看，有些教师擅长数学建模，有些教师擅长数学实验；第三，目前的课程设置仍然沿用了学科课程体系，虽然教育部在几年前就提出要开展信息技术和学科课程的整合，但到目前为止，在高职数学建模课程中还没有形成融合课程体系；第四，以“学科为中心”的观念仍然占有主导地位，以“学生为中心”的理念还没有落实。

误区二：分科教学。就是把数学建模课程与数学实验课程作为两门课程单独开设，任教数学建模课程的老师只讲建模方法，而对于模型求解的（计算机）方法却不讲；反之，任教数学实验课程的老师只讲模型求解的方法，而对于模型建立的方法却不讲。数学实验教师只要把前任教师的模型进行求解就完成了教学任务，而根据求解的结果对模型的有效性、合理性、稳健性、变量的误差和精度、变量的灵敏度等进行必要的分析这些环节就被取消了。

事实上，从数学建模的本质来看，很少有通过一次建模就能找到一个符合实际情况的数学模型。数学建模的魅力正在于根据实验的结果不断地改进模型，一步一步贴近实际走向成功，从而最终圆满地解决问题的。数学实验的内容仅仅剩下模型求解这样一个环节，使得学生丧失了体验数学建模的真正魅力的环节，也失去了培养分析、探究、优化模型的绝好机会。

成因：由于大多数数学软件都是英文版本，比如MATLAB软件、LINDO软件、LINGO软件等都是英文版本，这就给教师掌握和运用数学实验技术带来了障碍，导致教师数学实验能力不熟练，表现在以下几个方面：（1）在课堂上不能轻松驾驭实验平台，编写程序速度慢，浪费课堂上的宝贵时间，教学效率低；（2）当程序编写完成后出现不能运行的情况发生时，教师就无法寻找错误的原因并及时排除故障，从而导致模型求解失败，教师沮丧，学生失望；（3）尽管计算机已经返回了程序错误的原因和需要修改的地方，但由于返回的是英文，教师无法理解准确的意义，哪怕是很简单的程序错误，也因为不能理解真正意义而导致实验失败。为了避免出现课堂上实验失败或者操作低效的情况，干脆就指定一位教师去专门讲授数学实验，这样以来，讲授数学建模的教师就不讲授数学实验，同时，讲授数学实验的教师就不讲授数学建模。

误区三：“高效灌输”的授受式教学。 教学以讲授法为主，表面上好象按时保量完成了教学任务，相比探究式教学、研讨式教学等方式，显得“高效”，其实，学生并没有真正理解或掌握，教学效果大打折扣。经过很长一段时间的培训后，学生对实际问题，特别是结构不良问题的解决仍然感到无从下手；对于数学软件的实际操作，学生仍然难以独立地、顺利地、快速地编写程序。

成因：首先，数学建模要解决的问题大多数是结构不良问题，对这样的题目，学生感到没有现成的方法可以套用，感到无从下手；其次，由于学习平台没有建立起来，学生没有提前预习学习内容，在课堂上教师无法采用探究式、研讨式等自主学习的方式；第三，课时不足，没有充分的时间用来安排课堂讨论或者让学生自主练习。比如，数学实验这样的课程不是理论课的内容，不能由老师一讲到底，但现实情况是课时太少，内容太多，课堂上教师不得不一讲到底，至于操作练习就只能留给学生课后去练习了。

基于以上对数学建模和数学实验教学过程的反思，我们认为，现行的分科课程已经不能适应高职“工学结合”人才培养模式，只有将《数学建模》和《数学实验》两门课程进行整合，把两门课程的学科特点有机结合起来，才有望解决教学实践中出现的突出矛盾。

[1]进一步规范竞赛组织工作 不断提高竞赛质量[EB/OL].(2009-05-20)[2009-12-02]http://www.mcm.edu.cn/newsletter/letter2008/letter200803.pdf.

[2]宗 河.今年我国新设44种高职高专专业[N].中国教育报，2009-03-21.

[3]鲁志鲲. 结构不良问题解决研究述评[J].首都师范大学学报（社会科学版）,2006,(4).

The Teaching Reflection of Mathematical Modeling and Experimental Mathematics in Higher Vocational College

WANG Jijian, HAN Yixiu
(Zhejiang Industry & Trade Vocational College Wenzhou Zhejiang 325003)

At present there are three misunderstandings in “Mathematical Modeling” and “Experimental Mathematics” i.e.,repeated content, classified-subject teaching, high-efficiency giving and accepting style of teaching. The effective method to solve the above-mentioned problem lies in the integration of “Mathematical Modeling” and “Experimental Mathematics”.

Mathematics modelling; Experimental mathematics; Curriculum integration; Teaching reflection

G712

A

1672-0105（2010）01-0043-03

2009-12-20

浙江省2009年教育科学规划年度研究（重点）课题《高职数学实验与数学建模课程的整合研究》（SB26）.

王积建（1966- ），男，甘肃景泰人，副教授，硕士，主要研究方向：数学建模和数学教育研究。

[责任编辑：周宗谷]