改进的经验模式分解方法及其在图像边缘检测中的应用
2010-08-24郭艳光程显生
郭艳光,程显生
GUO Yan-guang, CHENG Xian-sheng
(内蒙古农业大学 职业技术学院 ,包头 014109)
0 引言
图像特征提取是图像处理的关键技术之一,图像边缘检测涉及图像中研究对象的特征提取,在实际的数字图像处理中,图像的边缘包含了图像的位置、轮廓等特征,是图像的基本特征之一,好的边缘检测算法对进行更高层次的图像分析、理解等有不可忽视的实用价值和影响。
传统的边缘检测算子中Roberts算子、Priwitt算子、Sobel算子、Canny算子等,将边缘点理解为灰度突变点,通过不同的算子提取。但是,噪声也是图像灰度变化中的高频成份,检测结果噪声较多;Gauss-Laplace和Canny算子较好的实现了图像边缘提取,但不能满足实际中对图像边缘提取的要求;还有小波方法、基于热传递方法、广义模糊算子方法等同样存在漏检边缘、模糊等缺陷。
二维经验模式分解方法在非平稳信号的处理应用中具有很多独特的优点。因此,把经验模式分解方法应用到边缘提取中,能提取出具有良好性质和结果的边缘。但经验模式分解最大的缺点是算法的时间复杂度大。本文将详细阐述EMD的原理及其实现方法,介绍一种快速经验模式分解方法并将其应用于图像边缘提取,将图像中的边缘快速有效的提取出来。
1 EMD原理
一维EMD的基本思想是:选取区域范围,从图像中找出信号中每个区域的局部极大值和局部极小值点,对极大值点和极小值点分别进行曲线插值,获得信号的上、下包络线,计算平均包络线,计算原信号与平均包络线的差值,然后利用筛选算法把符合模态函数(IMF)的信号分解出来。循环获得频率逐渐降低的多个模态函数。
模态函数必须满足:1)数据序列x(t)的极值点数目与零点数目之差少于2个,2)上、下包络的均值为零。第二个条件较为苛刻,将其用另外的标准代替:
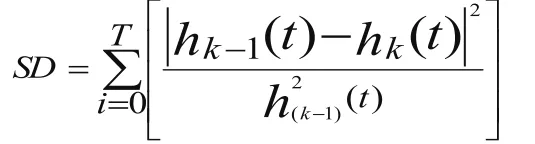
式中hk(t)是IMF分量提取模块中本次循环过程中求得的平均包络,hk-1(t)是上次循环过程中求得的平均包络,0……T是平均包络线所包含的时刻。SD值一般在0.2-0.3。
二维EMD分解实现过程:
1)对所给图像求取曲面局部极值点,包括所有局部极大值和极小值。
2)求取均值包络曲面。极值点选取之后,对各极大值点和各极小值点分别进行曲面拟合,经插值后得到极大值点曲面包络和极小值点曲面包络,将两曲面数据求平均得到均值包络曲面。
3)计算原始曲面与均值包络曲面。
4)与一维相似需计算终止条件。
重复步骤1~3,直到满足给定的终止条件得到第一个模态函数IMF1,用原图像减去第一个模态函数得到第一个残余(residue),对残余重复步骤1~步骤4,依次得到图像的N个固有模态函数和第N个残余。根据此方法对图像进行分解,结果为下图所示:





2 改进的BEMD
改进的BEMD原理:
目前,二维EMD已广泛应用在图像处理领域的诸多研究方向,也取得了一些可喜成果,但是二维EMD算法的时间复杂度一直是一个难以解决的问题,直接影响了它的应用范围。本文针对二维EMD算法中运行时间最长的求取上下包络进行改进,具体算法如下:
1)初始化r0(x,y)=f(x,y),N=1;f(x,y)是原图像,x,y是图像的大小,i是分解的IMF数目;
2)对所给图像求取曲面局部极值点,包括所有局部极大值max(x,y)和极小值min(x,y);
3)求第N个模态函数
(1)初始化: i=1,j=1,i,j为图像的大小,win=3,5,…,3+2N(N为分解的特征函数的个数);
(2)以点(i,j)为中心,覆盖到与它间距为(win-1)/2)的行和列中所有的点,构成win行win列矩阵(如果超出边界,则取边界值),计算矩阵中最大值和最小值的数目;
(3)如果局部最大值和最小值的数目相等,则计算该win行win列矩阵平均值avg。如果最大值和最小值的数目不相等,则win=win+2,跳转到2步,当win=3+2N时最大值和最小值的数目还不相等,则计算win行win列矩阵平均值avg(i,j);
(4)循环得到图像中每一点的平均值avg(i,j);
(5)IMF=r(i,j)-avg(i,j),求出第一个模式函数IMF;
4)循环得到i个IMF。改进的BEMD部分程序:
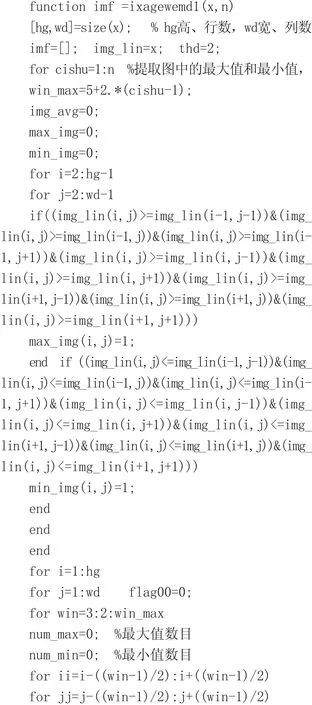


根据上述算法将图像进行二维EMD分解,得到N个IMF,结果如下图所示:

Image(128*128)

mode1

mode2

mode3

mode4

Image(512*512)

mode1

mode2

mode3

mode4
改进的BEMD算法避免了用插值方法求包络面,减少了时间复杂度,有效的增强了算法的可用性。
3 用改进的BEMD算法提取图像边缘
通过对图像进行分解得到多个模态函数,第一个模式中包含大多边缘信息,采用图像二值化方法或结合其他边缘检测算法提取边缘。本文采用改进的BEMD分解图像、二值化方法提取边缘(阈值为0)。
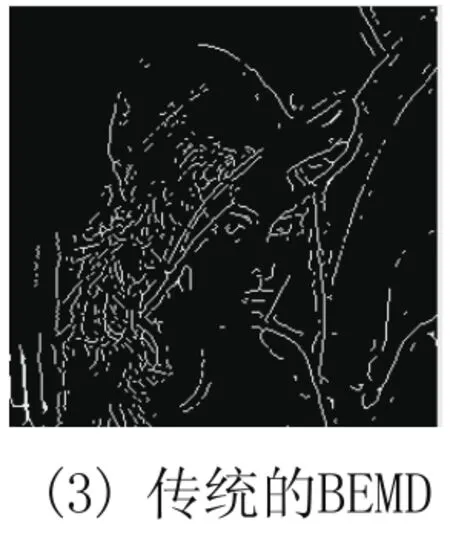
与传统边缘检测算法的比较结果如下图所示:图(1)采用Sobel算法,图(2)采用Canny算法,图(3)采用传统的BEMD算法,图(4)、(5)采用改进的BEMD算法。实验结果表明,采用改进的BEMD算法能更加清楚的提取边缘、算法效率较高。




4 结论
本文给出了经验模态分解(EMD)的实现方法,针对实现BEMD求取包络面时间复杂度大现象,提出了一种改进的BEMD算法,该方法避免了求解大型线性方程组以及大矩阵,降低了时间和空间复杂度,提高效率。实验结果证明了该方法的可行性和优越性。
[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decom position and the Hilbert spectrum for nonlinear and nonstationary times series analysis[J].Proc R Soc Lond A,1998,454:903-995.
[2] NORDEN E.HUANG,SHEN Z,Long S R.The Empirical Mode Decomposition Method and the Hilbert Spectrum for Non-Stationary Time Series Analysis[J].Proc.Royal.Soc.London A,1998,454(A):903-995.
[3] 米兰,许海波.基于边缘提取的图像拼接[J].计算机应用研究,2007,25(5):318-320.
[4] 沈滨,崔峰,彭思龙.二维EMD的纹理分析及图像瞬时频率估计[J].计算机辅助设计与图形学学报,2005,17(10):2345-2352.
[5] 张小蓟,张歆,孙进才.基于经验模态分解的目标特征提取与选择[J].西北工业大学学报,2006,24(4):453-456.
[6] 万 建,任龙涛,赵春晖.二维EMD应用在图像边缘特征提取中的仿真研究[J].系统仿真学报,2009,21(3):799-801.
[7] 宋立新,高凤娇,郗朝晖.二维EMD分解方法的比较与改进[J].电子与信息学报,2008,30(12):2890-2893.
[8] 刘忠轩,彭思龙.方向EMD分解与其在纹理分割中的应用[J].中国科学(E辑)—信息科学,2005,35(2):113-123.
