基于AMESim和SQP算法的爬行焊接机温控系统优化设计
2010-08-24张筱辰高宏力
张筱辰,高宏力,邓 鹏,郭 亮
ZHANG Xiao-chen, GAO Hong-li, DENG Peng, GUO Liang
(西南交通大学 机械工程学院,成都 610031)
0 引言
焊接是制造业中重要的工艺技术之一,近些年来的研究和应用成果表明,自动化焊接是保证焊接产品质量,提高焊接效率的可靠途径[1]。爬行焊接机是一种应用在工业生产现场的适用于PE土工膜等热焊性材料焊接施工的自动焊接机。由于爬行焊接机温控系统的重要组成部件——热楔具有储能特性,使得温控系统的稳态精度难以保证。并且爬行焊接机在实际工作时,温控系统不允许出现过大超调、系统响应要快、稳态温度上下偏差要求控制在1℃以内。因此,温控系统控制参数的选择直接影响焊接质量。
序列二次规划算法(简称SQP法)收敛速度快,效率高,是公认的最优秀的非线性约束算法之一。通过分析爬焊机温控系统参数和实际作业要求可知,爬焊机温控系统的参数选择可以归纳为一个求解非线性约束下的最优化问题。AMESim是法国Imagine公司推出的工程系统高级建模与仿真分析软件,它提供了一个系统级工程设计的完整平台,使得用户可以建立复杂的机电液一体化系统模型,并在此基础上进行仿真计算和深入的分析。针对爬焊机温控系统的特点,本文借助AMESim软件进行系统仿真与建模,并用SQP算法对温控系统的PID参数进行优化。
1 爬行焊接机温控系统设计
爬行焊接机的温控系统由直流稳压电源模块、温度控制模块、加热管驱动模块、加热模块、热电偶测温及其补偿模块组成。其中温度控制模块的处理芯片采用Atmel公司的AT89S52单片机,AT89S52是一种低功耗、高性能CMOS的8位微处理器,具有8K字节Flash。温度控制模块采用积分分离PID控制算法对加热管进行控制。
1.1 爬行焊接机温控系统组成及工作原理
本文利用AT89S52单片机实现对爬行焊接机加热温度的实时测量控制。温控系统控制框图如图1所示。安装在热楔内部的热电偶测量实际温度值并将其反馈到单片机中,单片机先将该反馈信号同温度设定值进行比较,然后用积分分离PID控制算法对系统误差进行处理,最后输出控制信号经加热管驱动模块对加热模块进行控制。从而起到调温作用。

图1 爬行焊接机温控系统控制框图
1.2 积分分离PID控制算法
系统中加入积分校正后,会产生过大的超调量。引进积分分离PID控制算法后,控制效果如图2所示。由图可知,采用积分分离算法既保持了积分环节,又避免了过大的超调。

图2 积分分离PID控制效果
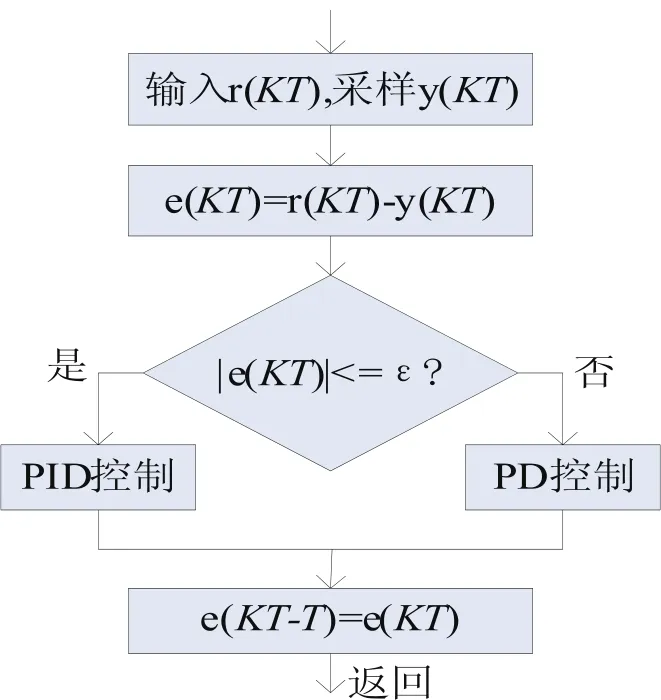
图3 积分分离PID算法流程图
积分分离PID的思想是人为的设定一个阈值ε(ε>0),当偏差|e(k)|>ε时,采用PD调节,当偏差|e(k)|<ε时,采用PID调节,算法流程图如图3所示。积分分离PID算法可用式(1)和式(2)表示[2]。

2 加热模块设计
加热模块由加热管和热楔两部分组成,结构如图4所示。爬行焊接机对材料进行焊接时,为了保证良好的焊接质量,焊接材料与热楔的不同接触点要求温度分布相等。本文采用ANSYS有限元分析软件对热楔不同点的温度分布进行了详细分析,通过优化热楔的结构尺寸,实现其温度分布达到工作要求,温度分布特性见图5。
2.1 加热管模型的建立
利用非接触式红外测温仪(希玛AR350)测量加热管在额定工作电压下,不同时间点的温度值,根据实际测得的数据,绘出如图6曲线:

图4 加热模块三维模型

图5 加热模块温度分布云图

图6 加热管温度-时间变化曲线
由加热管的温度-时间变化曲线可以看出,加热管的数学模型近似为一阶系统。一阶系统的单位阶跃响应是一条单调上升指数曲线,并最终维持在稳态值x(∞)。通过最小二乘法对采样数据进行处理后,可以得出时间常数T=35,故加热管的模型为1/(35S+1)。
2.2 热楔模型的建立
热楔相当于一个储能元件,具有积分环节的特性。积分环节的传递函数为1/Ts,其中 T是积分环节的时间常数。由积分环节的输入、输出关系可知:积分环节对阶跃输入,输出在t=T时等于输出。由能量守恒定律可得出如下公式:
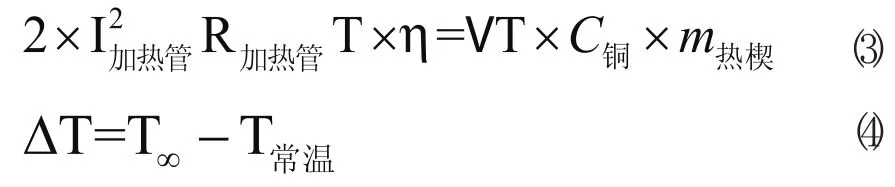
式中,通过加热管的电流I加热管=2A,单个加热管电阻R加热管=75Ω,T为时间常数,效率η=0.85,稳定温度T∞=282℃,常温T常温=25℃,铜的比热容C铜=0.39kJ/(kg·℃),热楔的质量m热楔=0.1kg。计算可得时间常数T=19.65。则热楔的模型为0.05/S。
3 序列二次规划算法
序列二次规划算法的基本思想是在每个迭代点构造一个二次规划子问题,将这个子问题的解作为迭代的搜索方向,并沿该方向进行一维搜索,逼近约束优化问题的解[3]。
约束非线性规划的数学模型通常表示为[4]:

式中f(x)为目标函数,每个等式和不等式为约束条件,f(x)和gi(x)为n元实值函数并且至少有一个是非线性的。序列二次规划(SQP)法就是在一点处用二次规划模型代替式(5),以一系列二次规划的解逼近式(5)的解,这样就使问题变得易于求解。其中,式(5)称为原问题,作为其近似的二次规划则被称为子问题。在SQP中,子问题的形式为
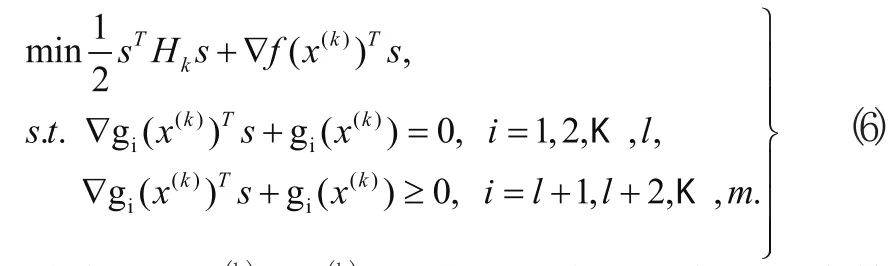
其中s=x-x(k),x(k)是n维欧氏空间Rn中的一个特定点,Hk是一个n阶实对称矩阵。子问题的库恩-塔克条件(KT条件)为
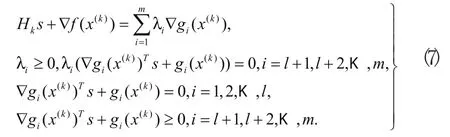
此不等式组的解记为(s(k),λ(k+1)),x(k)即是原问题的一个可供选择的解。
4 温控系统参数优化
根据上述计算的数学模型,在AMESim中建立如图7所示的爬焊机温控系统模型,系统在单位阶跃输入作用下产生偏差,经积分分离PID计算后,通过单相交流调压模块驱动加热管工作,加热管产生的热量传递到热楔后,安装在热楔中的热电偶采集实际温度值并经冷端自动补偿后反馈回来,同预设值进行比较,系统再经过处理,最终使实际温度等于预设温度并稳定输出。

图7 爬行焊接机的温控系统
1)用AMESim的批处理功能确定比例系数Kp,积分系数Ki,微分系数Kd这三个参数的大致范围。通过观察不同参数下曲线的输出结果,最终确定的参数范围是Kp(0~0.4), Ki(0~0.0005), Kd(0~20)。
2)确定系统的优化约束条件。经分析本文所述的加热管系统不允许出现过大的超调,爬焊机在实际的预热过程中允许的温度波动为5℃,最高温度为282℃,计算可得超调量MP约为2%。另外,爬焊机在工作前要预热2~3分钟,即爬焊机在120s的时候能够达到最高温度的80%以上即可正常的工作。
3)设置输出参数对话框,将 PID调节中的Kp、Ki、Kd设为输入参数,热楔模型输出OUTPUT、偏差ERROR作为输出量,要约束的量在复合输出参数中设置,超调量MP的表达式可写为max(0.0,-min_ERROR),min_ERROR的表达式为globMin(ERROR),系统在120s对应的温度值的表达式为valueAt( OUTPUT,120)。
4)选择AMESim中的设计开发模块,用SQP算法对PID参数进行优化。在设计开发定义对话框中分别按照批处理确定的参数范围定义各个输入参数的上限值和下限值。定义超调量的上限为0.02,系统在120s时达到最高温度值的80%以上。
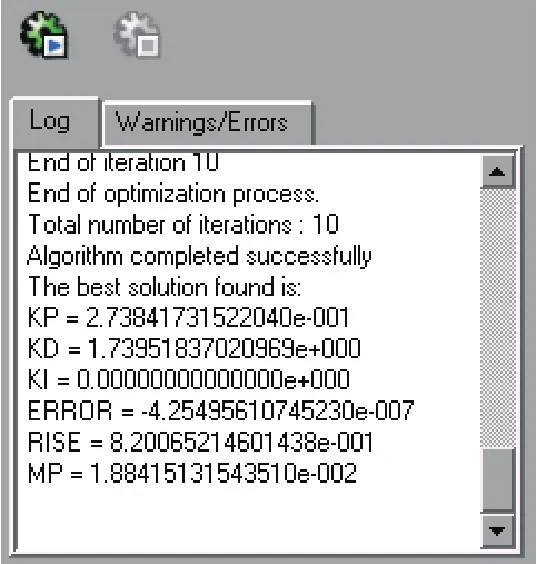
图8 参数优化结果
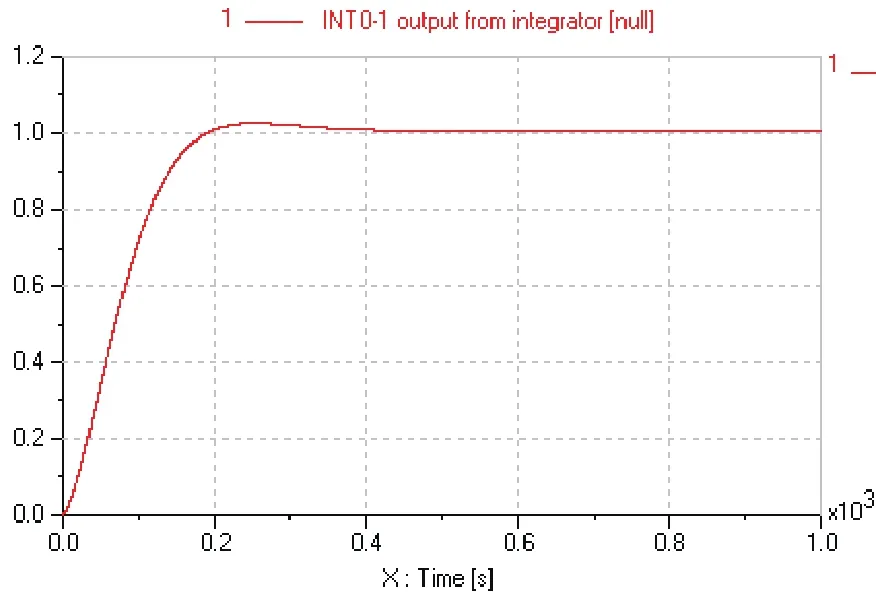
图9 优化后的阶跃响应
5)运行并查看优化过程。运行后的参数优化结果如图8所示,从优化结果可以看出,Kp=0.27、Ki =0、Kd=1.74。该优化参数下系统的阶跃响应如图9所示。从系统优化后的阶跃响应曲线可以看出优化结果非常好,超调小,响应快,达到了预期效果。
5 结论
本文分析了爬行焊接机温控系统的工作原理,并建立其AMESim仿真模型。借助序列二次规划(SQP)算法对PID控制器的控制参数进行了优化。该算法处理速度快,可靠性高,有效的提高了优化设计的效率。为解决同类控制系统优化问题提供了重要参考。
[1] 林尚扬,等.焊接机器人及其应用[M].北京:机械工业出版社,2000.
[2] 何克忠,李伟.计算机控制系统[M].北京:清华大学出版社,1998.
[3] 贾长治,郑坚.结构设计参数对火炮炮口振动影响的仿真及基于SQP方法的优化[J].机械工程学报,2006.
[4] 张忠桢.二次规划:非线性规划与投资组合的算法[M].武汉:武汉大学出版社.2006.
[5] 张俊俊,江玲玲.基于AMESim和遗传算法的液压位置伺服系统优化设计[J].机床与液压,2008.
[6] 付永领.AMESim系统建模和仿真[M].从入门到精通.北京:北京航空航天大学出版社,2006.
