基于正交试验设计的客车车身结构优化研究

崔 玲，高云凯

CUI Ling1 , GAO Yun-kai2

（1.山东交通职业学院，潍坊 261206；2.同济大学，上海 201804）

0 引言

汽车车身结构优化是汽车车身轻量化工程的主要方面之一。车身结构优化后，不仅可以节省材料、减轻自重，而且能提高整车的动力性和经济性并减少排放。但是，要同时保证车身结构在多种工况下的强度、刚度、NVH、疲劳等性能指标，进行车身结构综合优化分析是比较复杂的。目前，对多工况优化结果综合的方法有：将各工况优化结果取均等的权重进行综合，确定优化后结构参数值[1]；或取同一设计变量在几种工况优化结果中最大者作为最终的综合结果[2]。前者平衡考虑了各工况优化结果，但没有区别出各种工况优化结果对综合优化结果影响的差异性；后者最大程度上保证了综合后车身结构的强度、刚度，但没有达到轻量化的最优目的。总之，都不能最佳地实现车身轻量化。

本文首先应用MSC Nastran软件，分析了某客车车身骨架梁结构在四种不同工况下的优化截面尺寸[3-5]。然后采用正交试验设计方法[6,7]，分析了四种优化工况结果在综合优化分析中影响因素的大小及其在综合中各应占的最优权重，确定了该客车车身最优的综合优化方案。通过对综合优化后的车身结构进行强度、刚度和模态的分析校核，可以确认，在客车车身结构综合优化中引入正交试验设计方法，能够在确保大客车车身刚度、强度和模态等性能指标的前提下，实现结构多工况优化和车身结构的轻量化。

1 截面尺寸优化

考虑到客车实际运行工况要求及车身骨架的近似对称性，选取四种工况进行优化：弯曲工况、右前轮悬空工况、右后轮悬空工况、台架试验扭转工况。四种优化工况使用同一个优化有限元模型，约束和载荷处理根据各工况的要求及特点进行设置。

1.1 有限元模型

使用前处理软件MSC.Patran建立有限元模型，骨架有限元划分时采用基本单元尺寸为50mm的Bar单元，车身骨架底架焊接板的单元划分采用基本尺寸为50mm的shell单元。模型共有25926个单元，其中Bar单元14021个，shell单元11905个。有限元模型如图1所示。

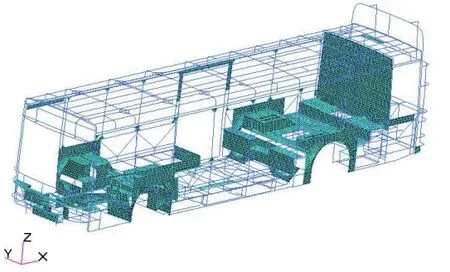
图1 优化分析有限元模型

1.2 优化参数的设置

四种工况的优化目标函数和设计变量的设置都是相同的。考虑车身轻量化目标，目标函数选为车身总质量最小。设计变量为梁截面的高和宽。其中，支架梁等一些非承载零部件，由于没有承载，在优化中易导致错误的截面尺寸减小，因此不作为设计变量；另外考虑到制造成本问题和优化方案可行性，底架截面尺寸较大的热冲压纵梁与横梁也不作为设计变量进行优化。考虑以上因素，该优化分析中共取了301组梁的截面宽和高为设计变量，共602个设计变量。

约束条件根据各工况特点及工程要求分别设置。在四种工况的优化中，约束所有梁的最大应力不超过215MPa。在台架试验扭转工况优化中，按照同级别大客车车身骨架的扭转刚度值77000Nm/deg约束前、后桥对应的车架位置Z向的位移为9.331mm。

1.3 优化结果分析

四种工况的优化结果都不相同，但都不同程度的实现了车身骨架结构质量的明显减小，同时也分别满足应力和挠度等约束条件。四种工况优化结果如表1所示。可见，同一设计变量在四种工况优化结果中的增减趋势不完全相同，每一工况优化结果只满足该工况的优化约束要求。为同时满足该客车实际运行多工况的要求，需要进行多工况优化的综合分析，采用正交试验设计方法，确定各工况优化结果在综合优化分析中的权重。

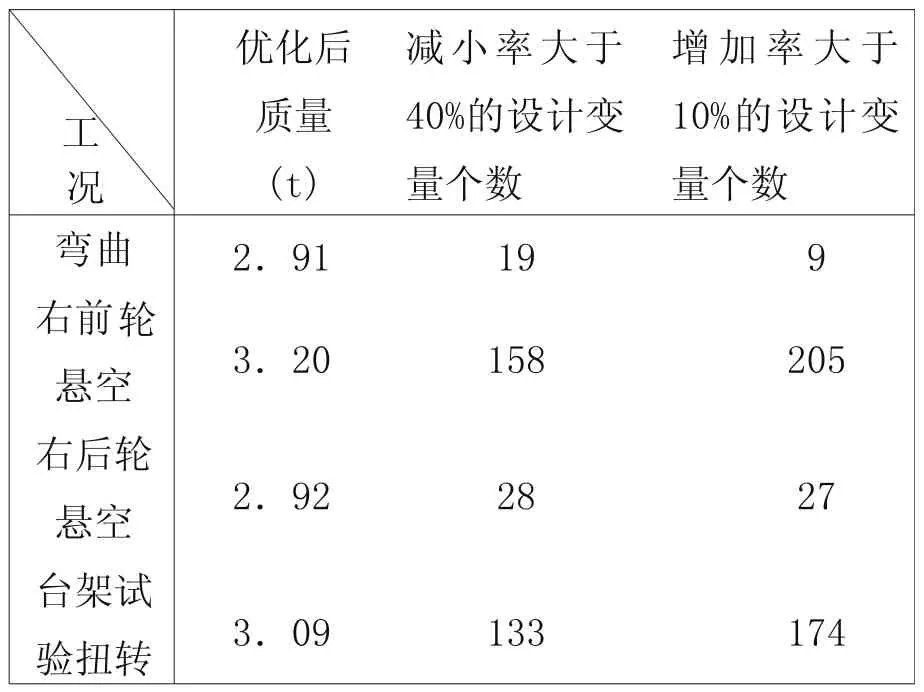
表1 四种工况优化结果

2 正交试验设计

所谓正交试验设计就是一种利用正交表来合理地安排试验，利用数理统计的原理科学地分析试验结果，处理多因素试验的科学方法。这种方法的优点是，能通过代表性很强的少数次试验，摸清各个因素对试验指标的影响情况，确定因素的主次顺序，找出较好的生产条件或最优参数组合。经验证明，正交试验设计是一种解决多因素优化问题的卓有成效的方法。而正交表是运用组合数学理论在拉丁方和正交拉丁方的基础上构造的一种表格，它是正交设计的基本工具，它具有均衡分散，整齐可比的特性。

2.1 正交试验设计方案

试验指标设为车身骨架质量，因素设为弯曲、右前轮悬空、右后轮悬空、台架试验扭转四种工况的优化结果，水平设置为每种工况在综合分析中所占的权重。由于四个因素的权重之间存在线性关系，又根据L9(34)的特点，首先选取了三水平三因素，即选择正交表L9(33)的前三列，三因素为弯曲、右后轮悬空、台架试验扭转工况的优化结果，如表2所示；三因素的三水平设置如表3所示，通过弯曲、右后轮悬空、台架试验扭转权重系数的线性关系即得到每组试验中右前轮悬空工况优化结果在综合分析时的权重系数，试验设计方案如表4所示 。

表2 选用的正交表L9(33)

表3 各因素水平

表4 试验设计方案

2.2 试验结果分析

用各工况的优化结果乘以权重得到每次试验的综合值，在MSC.Patran软件中将综合后的截面尺寸附给相应的梁杆件，得到每次试验的车身骨架质量。试验结果如表5所示。由表5可以看出，弯曲和右后轮悬空列的正交试验极差都较大，说明弯曲工况和右后轮悬空工况因素水平的变化对试验指标的影响较大。试验指标车身骨架质量是越小越好，因此对于每种因素不同水平对试验指标的影响程度分析如下：第1列即弯曲工况第3水平所对应的数值3.035为最小，所以取它的第3水平最好；第2列即右后轮悬空工况第1水平所对应的数值3.038为最小，所以取它的第1水平为最好；第3列即台架试验扭转工况第1水平所对应数值3.061为最小，所以取它的第1水平为最好。最优的试验设计结果是弯曲、右后轮悬空、台架试验扭转工况权重分别为0.3、0.4、0.3，相应的前扭工况权重为0。但这种组合不在所选择的九个试验中，故对该组合进行一次试验得到试验后的车身骨架质量为2.959t，优于正交表所列的9次试验结果，可认为该组合为最优方案。

由于上面的正交试验只研究了弯曲工况、右后轮悬空工况、台架试验扭转工况不同水平对试验指标的影响，无法得到右前轮悬空工况的不同水平对试验指标的影响趋势，因此进行了第二次正交试验，试验的过程同上面试验，只是正交表中的1、2、3 因素改为弯曲、右前轮悬空、右后轮悬空，其他设置如前，台架试验扭转工况的权重由其与弯曲、右前轮悬空、右后轮悬空工况的线性关系确定。试验结果表明右前轮悬空工况试验指标的较优水平为其最小水平。

表5 正交试验设计结果分析

由上面两次正交试验分析可知，对四种工况下优化结果进行综合的最优方案为：弯曲工况占30%、右前轮悬空工况占0%、右后轮悬空工况占40%、台架试验扭转工况占30%。

3 综合优化分析

取前面正交试验设计得到的最优综合方案，将综合后的截面尺寸附给相应的梁杆件，得到最优综合方案下该车车身骨架质量为2.959t。对车身骨架模态较灵敏部件的截面尺寸进行加强，并根据工程要求对截面尺寸进行规范化处理，对修改后模型的模态、刚度、强度进行反复校核，直至满足各项指标。优化前、后，模型模态、刚度、强度性能对比见表6。

由表6可以看出，采用正交试验设计方法确定各工况优化结果的权重，进而进行综合优化分析后，车身骨架的一阶扭转和一阶弯曲模态都有所提高，优化前车身骨架应力较大的部件也得到了加强，最大应力值得到有效降低，扭转刚度值较优化前低但仍处于客车扭转刚度合理范围之中。

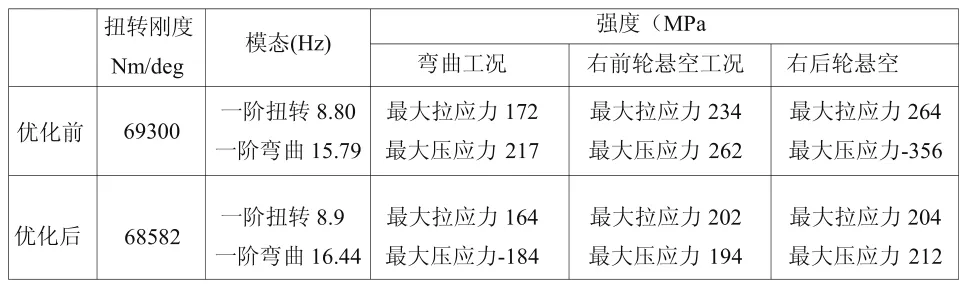
表6 优化前、后模型模态、刚度、强度性能对比

4 结论

1）使用正交试验设计方法可以合理确定大客车车身多工况优化结果在综合分析中所占的最优权重，为多工况车身结构优化结果的综合分析提供了一种方法。将正交试验设计法用于结构优化分析中有利于实现车身结构的轻量化。

2）在进行客车车身骨架结构的综合优化时，分别按40%、30%、30%的权重考虑右后轮悬空、弯曲及台架试验扭转工况，即可在满足刚度、强度要求的条件下实现车身骨架质量明显下降。

[1] 江峰.城市公交大客车车身结构分析与优化研究[D].上海：同济大学,2007.3.

[2] 高云凯,姜欣,张荣荣.电动改装轿车车身结构优化设计分析[J].汽车工程,2005,27(1)：115-117.

[3] T.Kim.Study on the optimization of bus body structure.SAE 923953.

[4] 隋允康,等.MSC.Nastran有限元动力分析与优化设计实用教程[M].北京：科学出版社,2004：166-168.

[5] 徐宏兵,葛如海,王怀.大客车车身骨架轻量化改进设计[J].江苏大学学报(自然科学版),2003,24(6)：25-28.

[6] 曾小华,王庆安,等.正交优化设计理论在混合动力汽车设计中的应用[J].农业机械学报,2006,37(5)：26-28.

[7] 陈魁.试验设计与分析[M].北京：清华大学出版社,2005.