三种估计疲劳极限方法的比较

朱学超，李泉珍

（贵州大学土木建筑工程学院，贵州 贵阳 550003）

疲劳极限是表征材料与结构疲劳性能的重要参量之一，其试验与测定方法一直受到国内外的关注。当研究其概率值时，试验方法主要有大子样升降法和小子样升降法。大子样升降法测定结果精度较高，但花费试样较多，一般大于30个，这一试验方法已写入了英、日、法等国的试验标准。小子样升降法测定结果精确度稍差，但花费试样较少，约 13个～20个，在我国得到了广泛应用。

疲劳极限的早期理解是，材料不发生疲劳损伤（无限疲劳寿命）的临界疲劳强度；后来被理解为一定疲劳寿命（如 107循环数）下的中值疲劳强度估计值。因材料的疲劳极限随加载方式和应力比的不同而异，通常以对称循环（即应力比R=－1）下的疲劳极限作为材料的基本疲劳极限。［1］扩展到概率领域，则应理解为一定疲劳寿命下疲劳强度的概率（包含存活概率和置信度两方面含义）估计值。本文阐述了3种估计计算方法，并进行了比较。

1 加权平均法

为了区别对待不同精度条件下的测量结果，在计算平均值时需要采用加权平均。所谓权，就是权衡轻重的意思，某个测量值越可信赖，则在数据分析中应该使它占有越大的比重，即需要赋予它越大的权。测量值的可信赖程度与测量值的误差密切相关，误差越小，可信赖程度就越高，权也就越大；反之亦然。在加权平均时，习惯上将权值取得与测量结果的方差成反比。采用加权平均法对其小子样升降法的疲劳试验结果进行处理时，其缺点是加权平均值只可以作为可靠度为50%的疲劳极限。

2 正态分布（或对数正态分布）估计疲劳极限应力值［2］

在疲劳分析中，需要利用由各种试验获得的疲劳性能数据。由于疲劳试验数据常常有很大的分散性，因此，只有用统计分析的方法处理这些数据才能够对材料或构件的疲劳性能有比较清楚的了解。

正态分布也称高斯（Gaussian）分布。对数疲劳寿命 lgN常常是服从正态分布的。令X＝lgN，即可利用正态分布理论进行对数疲劳寿命X的统计分析。

2.1 正态分布的密度函数和分布函数

若随机变量X服从正态分布，则密度函数（或称频率函数）为：

式中，μ为母体均值；σ为母体标准差，是非负的。正态概率密度函数曲线是关于x＝μ对称的，两端伸向无穷。f（x）在x＝μ处取最大值，且可见，σ越小，在x＝μ附近取值的可能越大；密度函数曲线越“瘦”，随机变量X的分散性越小，故标准差σ反映了X的分散性。

一般来说，无论分布形式如何，概率密度函数均具有以下性质：

（1）f（x）≥0。f（x）表示随机变量X取值为x的频繁程度，故对于所有的可能取值，f（x）显然是非负的。

正态概率分布函数为：

分布函数F（x）给出了随机变量X取值小于等于x的概率。显然可见，随机变量X取值大于x的概率则为1－F（x）。

2.2 给定疲劳寿命下的破坏概率估计和置信水平

在对数疲劳寿命服从正态分布的假设下。首先，应确定分布参数，即均值µ和标准差σ。µ、σ是母体分布参数，其真值常常是得不到的。一般只能由取自该母体的若干试件组成的“子样”（或称样本）试验数据来估计。

子样均值 为：

式中，xi为第i个观测数据，对于疲劳分析，则是第i个试件的对数寿命，即xi＝lg Ni；n为子样中xi的个数，称为样本大小（或样本容量）。

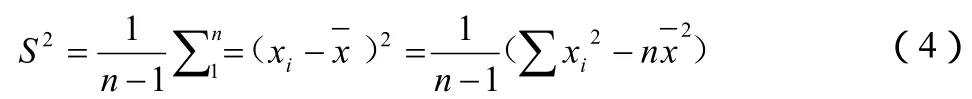
子样方差S2为：方差S2的平方根s，即子样标准差，是偏差的度量，反映了分散性的大小。注意到（4）式，所有n个偏差的总和为零，故只有（n－1）个偏差是独立的。

子样大小n越大，子样均值x和标准差s就越接近于母体均值µ和标准差σ。因此，假定对数疲劳寿命X＝lgN是服从正态分布的，则只要由一组子样观测数据计算出子样均值和标准差s，并将它们分别作为母体均值µ和标准差σ的估计量，即可得到具有某给定破坏（或存活）概率下的寿命或某给定寿命所对应的破坏（或存活）概率。

事实上，这样估计的对数寿命Np＝＋up·s（其中 up为与破坏概率p对应的标准正态偏量，其存活率即可靠度R＝1－p），可能比母体对数寿命的真值µ＋up·σ小，也可能比母体真值大。因此，需要引入置信度γ这一概念。如果由＋up·s估计的破坏概率为p的对数寿命小于真值的概率为γ，则称γ为这一估计的置信度。置信度γ通常取为90 %或95 %。将破坏概率为p，置信度为γ的对数寿命写为：

式中，k称为单侧容限系数。

由此，可以求出一定可靠度R和置信度γ下的疲劳极限。

3 三参数威布尔分布理论［2、3］

在疲劳强度的可靠性设计中，最适合表达疲劳强度分布的函数，除了正态分布函数外，还有目前发展起来的威布尔分布概率密度函数。威布尔分布概率密度函数的优点，在于存在最小寿命，即100 %可靠度的寿命，这是符合疲劳破坏实际情况的。

3.1 威布尔分布的密度函数和分布函数

威布尔分布的密度函数为：

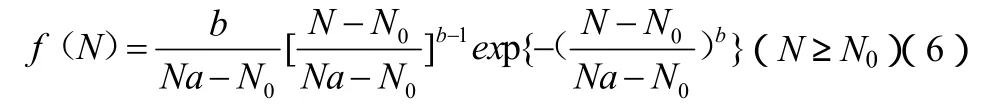
式中，N0、Na和b为描述威布尔分布的3个参数。N0是下限，也称为最小寿命参数；Na控制着横坐标的尺度大小，反映了数据N的分散性，称为尺度参数；b描述分布密度函数曲线的形状，称为形状参数。

如同前面讨论正态分布一样，我们关心的是在疲劳寿命 N之前破坏的概率，或寿命小于等于N的概率F（N）。由此有威布尔分布的分布函数为：

令 x＝（N－N0）/（Na－N0），则有 dN＝（Na－N0）dx，并注意到F（N）＝F（x），即得三参数威布尔分布函数F（N）为：

由上式显然可知，当N＝N0时，F（N0）＝0，即疲劳寿命小于N0的破坏概率为零，故N0是最小寿命参数；当N＝Na时，F（Na）＝1－1/e＝0.632，即疲劳寿命小于 Na的破坏概率恒为63.2 %而与其它参数无关，所以Na也称为特征寿命参数。

3.2 威布尔分布参数的估计

正态分布母体的均值µ和方差σ2都能直接反映在正态分布概率密度函数中。但在威布尔分布概率密度函数中并不包含 µ和σ2。因此，只能通过威布尔的三个参数N0、Na和b来表达µ和 σ2值。

引入伽马函数，设z＞0，定义伽马函数［4］（Γ－函数）为：

且有如下性质：①Γ（z＋1）＝zΓ（z）；

根据求数学期望的定义，通过积分计算可得威布尔变量的数学期望，即母体均值µ为：

威布尔变量的方差σ2为：

其置信度γ＝1－α（α是显著度）。

由此，便可求出一定可靠度和置信度下的疲劳极限。

4 结论

本文阐述了3种估计疲劳极限的方法。加权平均法简单易行，但缺点是加权平均值只可以作为可靠度为 50 %的疲劳极限。按正态分布（或对数正态分布）可以求出一定可靠度R和置信度γ疲劳极限，但它存在一个缺点，即当失效概率很小时，疲劳寿命或疲劳极限趋于零，这与很多试验结果和实际不符。而三参数威布尔分布中的参数 N0在疲劳试验中表示最小寿命或最低疲劳极限，与实际疲劳特性相符。

三参数威布尔分布理论与加权平均法相比，不仅考虑置信度，还可以求出任意可靠度下的疲劳极限。与按正态分布（或对数正态分布）相比，能更准确地估计疲劳极限，应用更广泛。

1 周传月、郑红霞、罗慧强.MSC.Fatigue疲劳分析应用与实例.北京：科学出版社，2005.3

2 陈传尧.疲劳与断裂.武汉：华中科技大学出版社，2002.1

3 李舜酩.机械疲劳与可靠度设计.北京：科学出版社，2006.9

4 吴 翊、李永乐、胡庆军.应用数理统计. 北京：国防科技大学出版社，2005.8