供水系统水泵装置更新维护费用的优化分析

王晓杰，程洪霞

（太原理工大学水利科学与工程学院，山西 太原 030024）

供水系统作为一种提水排水或补给水源的水利系统工程，在水资源调配、跨流域引水、城市及工农业供水等方面举足轻重，是解决水资源分布地域差异的有效系统工程。为保证供水系统的安全和稳定运行，必须对供水系统中的各项装置进行适时的更新维护，而水泵作为供水系统的主体，其更新维护决策显得尤为重要。本文给出了供水系统中水泵更新维护费用的经济优化分析，以期在保证供水系统安全稳定运行的条件下，降低成本，提高供水系统的总效益。

1 水泵的更新与维护

水泵的更新即购买新的水泵装置需要支付购买费。在水泵的折旧年限内，每年的购买价格有所不同，呈增加趋势。

水泵的维护主要包括：（1）叶轮：①叶轮叶片与叶轮室的间隙测量；②叶轮和叶轮室汽蚀、磨损检查及处理；③叶轮静平衡试验；④叶轮叶片密封装置的检查、更换、试验；⑤叶轮体耐压、密封试验；⑥叶轮叶片接力器的修理或更换。（2）泵轴：①泵轴变形和轴颈、轴承磨损程度；②轴承间隙的测量、调整；③同轴度的测量与调整。（3）泵壳和悬架：主要检测泵壳和悬架的锈蚀、裂纹、变形、损坏等情况。

水泵的维护需要支付相关的设备、实验和人工等费用，随着水泵使用时间的增长，每年所需的维护费用也在增加。

水泵的更新与维护都需要资金的投入，如何以最少的资金投入获得同样的效益，是值得泵站管理者及相关工作人员关注的一个重要问题。本文将该问题归结为图论中的最短路问题。

2 最短路问题的数学模型

2.1 最短路问题的基本思想

最短路问题就是在一个网络图中，给定一个起点，求出该起点到另一终点的权数最小的通路。最短路问题是网络理论中应用最广泛的问题之一。

最短路问题的一般提法如下［1］：设G=（V，E）为连通图，图中各边（vi，vj）有权 lij（lij=∞表示 vi和 vj间无边），vs、vt为图中任意两点，求一条道路μ，使它是从vs到vt的所有路中总权最小的路，即最小。

2.2 最短路问题的求解方法

最短路问题的求解方法有：Dijkstra算法、逐次逼近算法和Floyd算法等。其中Dijkstra算法由Dijkstra于1959年提出，可用于求解指定两点vs和vt间的最短路，或从指定点vs到其余各点的最短路，目前被认为是求无负权网络最短路问题的最好方法。

Dijkstra算法的基本步骤［1］如下：

采用标号法，可用两种标号：T标号和P标号，T标号为试探性标号（tentative label），P标号为永久性标号（permanent label），给vi点一个P标号时，表示从vs到vt点的最短路权，vi点的标号不再改变。给vi点一个T标号时，表示从vs到vt点的估计最短路权的上界，是一种临时标号，凡没有得到P标号的点都有T标号。每一步计算都把该计算点的T标号改为P标号，当终点vt得到P标号时，计算过程结束。

计算步骤：

（1）给vs以P标号，P（vs）=0，其余各点均为T标号，T（vi）=+∞。

（2）若vi点为刚得到P标号的点，考虑这样的点vj∶（vi，vj）∈E，且 vj为 T 标号，则 vj的 T 标号为：T（vj）=min［T（vj），P（vi）+lij］。

3 实例仿真与分析

现以某型号离心泵（一台）为例进行分析。每年年初做出购买决定，若购买新的水泵，要支付购买费，若使用旧的水泵，要付维护费。在购买新泵的第二年不考虑更换，因为泵正常运行的情况下，经过合理的维护，其运行效率不会有明显降低。［2］制定一个 12年的更新计划（对于离心泵，其折旧年限为 12年［3］），使总支出费用最少。

根据多年来该水泵的价格走势，对未来的价格做出预测，以等差数列的形式表示购买费。每年基本折旧率按8.08 %计算，每年平均大修理费按6 %计，净残值占原值按3 %计，［3］可得出水泵的维修费与余值，见表1。

考虑到水泵更新的当年旧水泵不一定能够卖出，例如用了一年后的水泵如果没有卖出，即实现不了4 596元的余值，但水泵仍可实现最终的残值150元，所以采用余值的期望收益来表示。

一个决策变量的期望值，就是它在不同自然状态下的损益值（或机会损益值）乘相对应的发生概率之和，即式中， )(Eja表示变量aj的期望值，Vij表示变量aj在自然状态θi下的损益值（或机会损益值），)(Piθ表示自然状态的θi发生概率。［4］这里取余值变现的概率为0.9，余值未变现的概率为0.1，可得到各年份期望余值（见表1）。

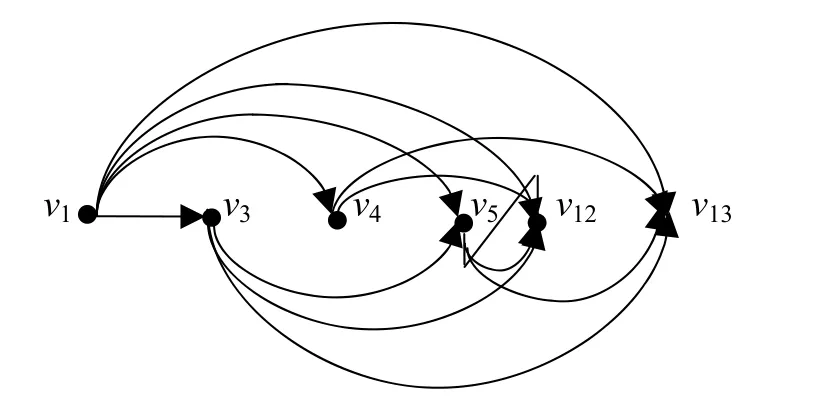
图1 路径示意图

该问题的路径见图1，用点vi表示第i年年初购进水泵装置，虚设一点v13，表示第12年年底。边（vi，vj）表示第i年年初购进的水泵装置使用到第j年年初，即第j－1年年底。

边（vi，vj）上的权重表示第i年年初购进的水泵装置，使用到第j年年初所需支付的购买和维护的全部费用（由表1计算得到）。例如（v1，v3）边上的1 357是第一年初购买费5 000加上两年的维修费50、95，减去第2年水泵装置的余值3 788；（v3，v6）边上的1 961是第三年初购买费5 100加上3年维修费50、95、140，减去水泵余值3 424。同理，可得各边上的权重（见表2）。

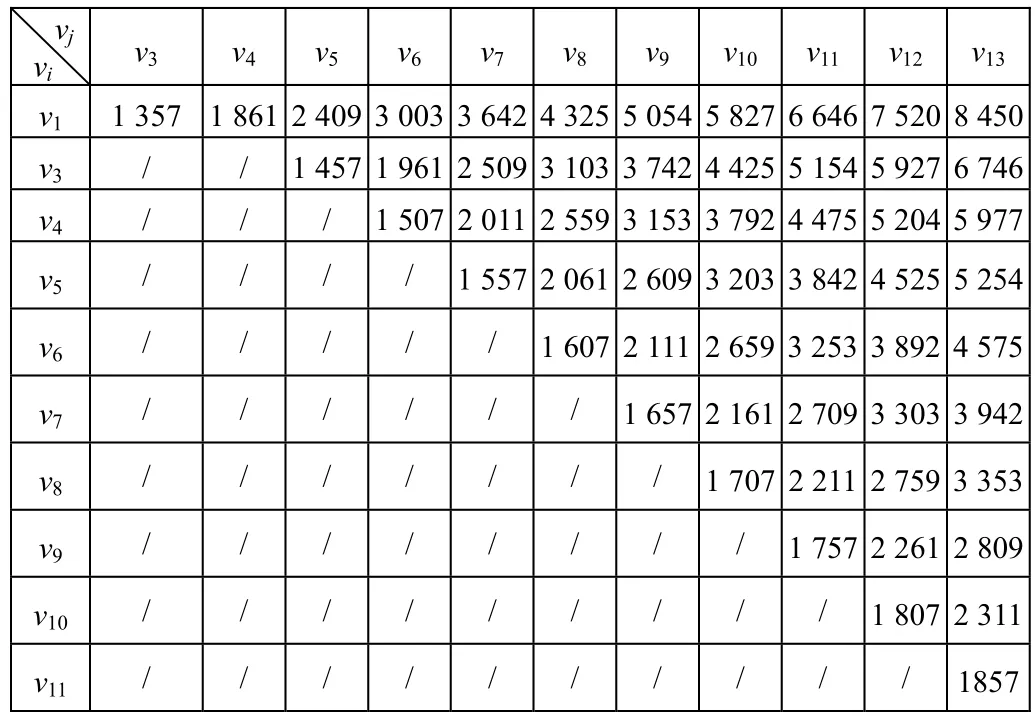
表2 边（vi，vj）上的权重lij （元）

运用Dijkstra算法作如下计算：

（1）首先给v1以P标号P（v1）＝0，给其余所有点T标号，T（vi）＝+∞（i＝2，3，…13）。

（2）v1为刚得到P标号的点，考虑点v1，有：T（v3）＝min［T（v3），P（v1）+l13］＝min［+∞，0＋1357］＝1357。

同理可得：T（v4）＝1 861；T（v5）＝2 409；T（v6）＝3 003；T（v7）＝3 642；T（v8）＝4 325；T（v9）＝5 054；T（v10）＝5 827；T（v11）＝6 646；T（v12）＝7 520；T（v13）＝8 450。

（3）比较所有T标号，T（v3）最小，所以令P（v3）=1 357，并记录路径（v1，v3）。

依此类推，可得计算结果见表3。

表3 最小路径记录表

综上所述，从v1到v13的最短路为v1→v6→v13，路长为7 578。所以决策者可以选择的方案为：在第一年初和第六年年初购进新水泵，在其余年份进行合理维护。此方案总支出费用为7 578元。

4 结束语

本文针对供水系统中水泵装置的更新维护费用问题，主要做了以下工作：①建立了网络理论中的最短路优化数学模型；②根据模型得出水泵装置更新维护的经济费用，并提供了最优决策方案；③考虑到余值变现的不确定性，运用概率的思想，采用期望余值的方法。通过以上的决策模拟过程，可以为供水系统中水泵装置的更新维护提供更经济合理的方案，从而为供水系统安全稳定运行节约成本，提高其总效益。另外，文中实例的数学模型是在水泵正常运转的条件下建立的，对于事故水泵以及实际中余值变现的概率，决策者应根据实际情况作具体分析，从而实现在确保水泵装置安全运行的条件下更新维护费用最低的目标。

1 胡运全主编.运筹学教程（第2版）.北京：清华大学出版社，2003

2 赵玉香.水泵修复与涂护工艺的方法探讨.中国农村水利水电，2008.4：113～114

3 武汉水利电力大学主编.泵站技术管理规程（SL255－2000）.北京：中国水利水电出版社，2000

4 张所地著.管理决策论.北京：中国科学技术出版社，2005