基于Hopfield网络模型的A/D转换器设计
2010-08-23李素文陈得宝杨一军
李素文,陈得宝,杨一军,赵 鑫,邵 芬
(淮北师范大学物理与电子信息学院,安徽淮北 235000)
在我校电气信息类专业的课程教学中,模拟量转换为数字量(A/D转换器)的原理分析以及相关的电路设计,在多门课程中作为主要内容被介绍。比如“电子线路”[1]、“数字电路”[2]、“电子线路的设计与实践”以及“通信原理”[3]中的模拟信号的数字传输等。而Hopfield神经网络是反馈式网络的一种,它具有一般非线性系统动力学系统的许多性质,如稳定问题,各种类型的吸引子以至混沌现象等,它是一种能利用这些性质来完成各种复杂计算功能的网络[4]。由于Hopfield网络收敛于其能量函数的极小值[5],且采用并行方式工作,有很强的并行计算能力和良好的实时性,我们可以用来设计最佳的A/D转换器。
1 连续性Hopfield网络模型
连续性Hopfield网络的模型结构如图1所示,每个运算放大器及其相关的电阻/电容网络代表一个神经元。运算放大器的输入/输出特性为s函数。Ii为外加的偏置电流,起神经元阈值的作用;wij为电导值,是第i个放大器与第j个放大器的反馈系数,wij=1/Rij。这里Rij是反馈电阻,yi是输出电压,=-yi;电阻ri和电容Ci并联实现时延,一般ri是运算放大器的输入电阻,电容Ci为分布电容。
设ui为第 i个放大器输入节电的电压。根据KCL定律的电流定律可推导出Hopfield模型的运算方程:

图1 连续性Hopfield网络模型
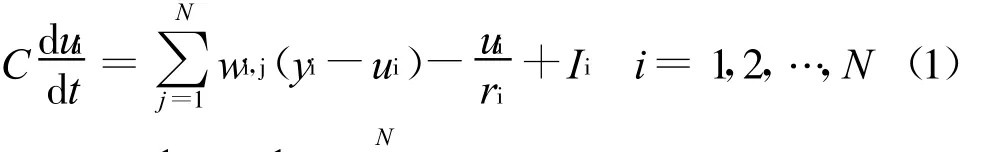

放大器的传输函数通常是一个s函数。s函数及其反函数我们都假设为增函数。
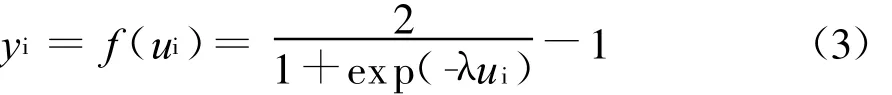
定义能量函数E为
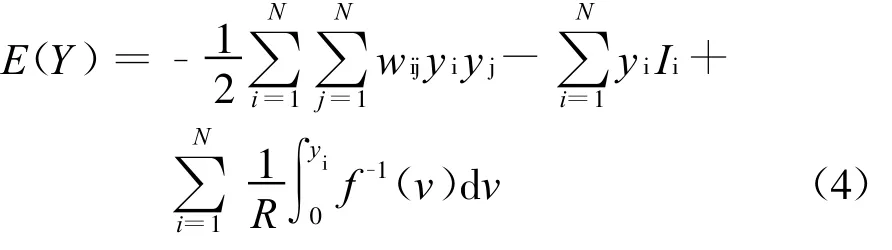
如果wij=wji,wii=0,则网络按能量函数E向减小的方向演化。
2 利用Hopfield网络设计A/D转换器
连续型Hopfield网络收敛于其能量函数的极小值,这使它能作优化计算。对于满足一定约束条件的优化问题,可以将约束条件包含于代价函数中,只要将优化问题的代价函数映射成网络的能量函数,就可以求出网络函数。设计的单层反馈4位A/D转换器电路如图2所示。A/D转换器的参数为
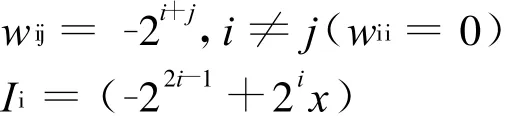
图2中用小黑圆圈表示连接电导值,x输入为电压值。该A/D转换器的优点是并行工作速度快,需要的运算放大器数目较少,电路结构简单。
但是,在选定了x的情况下,网络的能量函数存在多个极小点,其中一个是全局最小解。为了解决A/D转换网络存在多个稳定点问题,可以通过采用具有唯一平衡点的下三角互联网络,其网络参数为
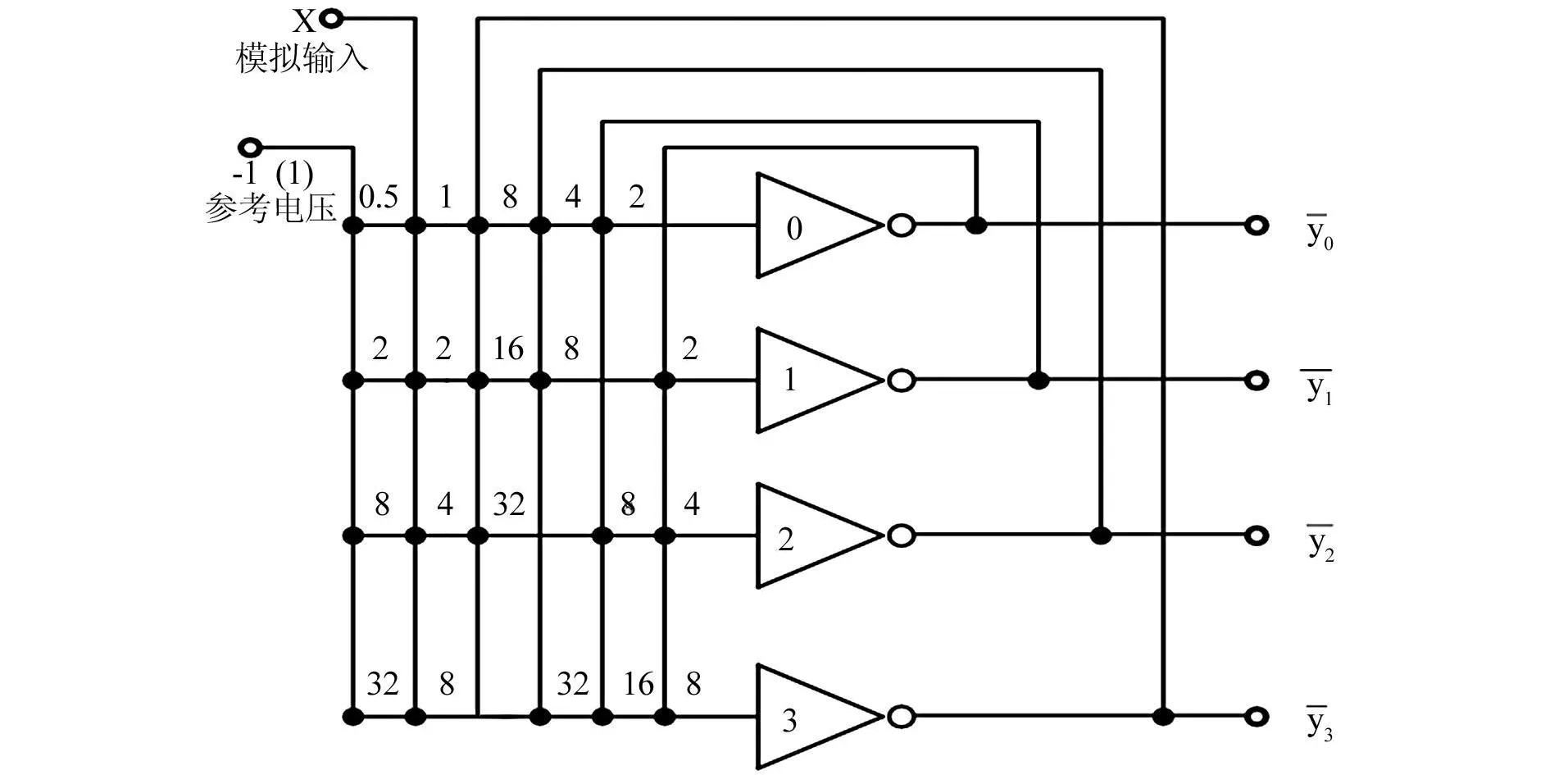
图2 单层反馈4位A/D转换器
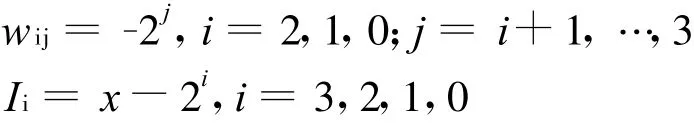
这样由Hopfield网络便得到一个A/D转换逐位比较法的模拟电路实现,如图3所示。
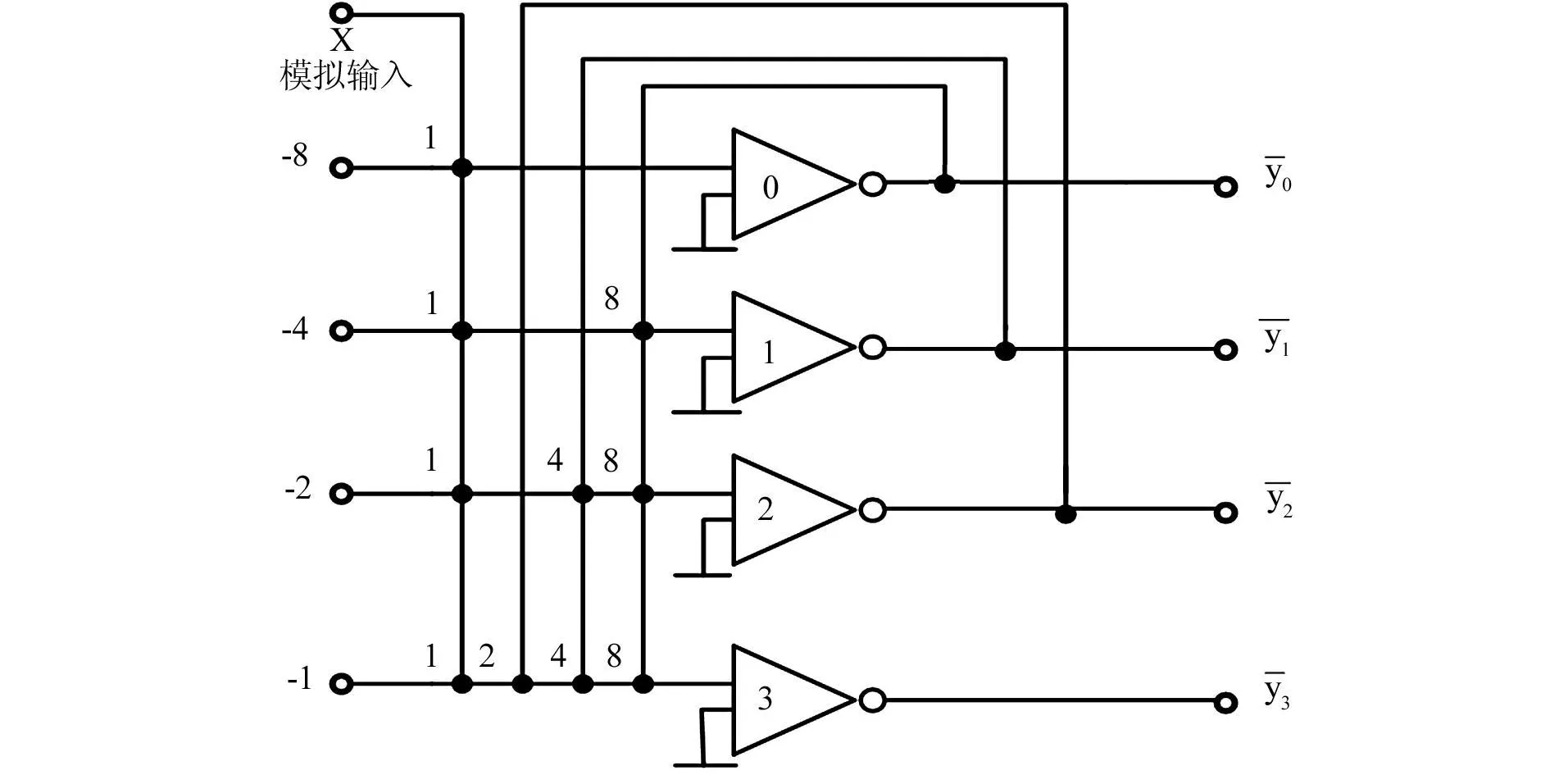
图3 A/D转换逐位比较法的模拟电路实现
3 结语
本文研究了Hopfield网络模型,并利用该网络收敛于其能量函数最小值的特性,设计了单层反馈4位A/D转换器电路和逐位比较的A/D转换器。这样不仅可以加深学生对A/D转换器的理解,而且对于Hopfield网络结构和特性也有所了解。在电气信息类专业学生的综合性课程设计中,很多学生都利用A/D转换模块,结合单片机实现了复杂的电路功能。因此笔者把科研意识引入到电气信息类专业的课程教学中,扩展学生的知识面,并增强他们的创新能力,为以后从事科研工作打下了坚实的基础。
[1] 谢嘉奎,电子线路[M].北京:高等教育出版社,2007
[2] 阎石,数字电路[M].北京:高等教育出版社,2008
[3] 樊昌信,通信原理[M].北京:高等教育出版社,2008
[4] 樊社民,邱关源.神经网络 A/D转换器电路的两种改进方法[J].北京:电子学报,1994,22(2):53-60
[5] 曾结昭,文卉,谢文彪,一种基于神经网络算法的频谱分析方法[J].南京:电气电子教学学报,2009,31(3):60-63
