电流斩波控制条件下影响开关磁阻电机转矩脉动的结构因素分析

2010-08-18袁龙生赵朝会

电气技术 2010年11期

袁龙生赵朝会张迪

（上海电机学院电气学院，上海 200240）

1 引言

开关磁阻电机（Switched reluctance motor，以下简称：SRM）及其驱动系统因结构简单、工作可靠、效率高和成本低等优点，近年来在电气传动领域得到广泛应用。但是由于 SRM 双凸极结构的特点，转矩脉动大，从而限制了其在调速领域的进一步的应用[1]。因此SRM转矩脉动的研究成为当前的一个热点，文献[2]采用电流幅值斩波控制策略来减小转矩脉动；文献[3]提出了 SRM 的转矩矢量控制概念及其控制策略来抑制开关磁阻电机的转矩脉动；文献[4]则是增加定子凸极宽度以及对应的定子凸极数目，达到降低SRM转矩脉动的目的；文献[5]利用非线性方法全面计算和分析了电机结构参数在角度位置控制条件下对转矩波动的影响。

由于SRM在恒转矩区，电机转速较低，电机反电动势小，为避免过大的电流峰值，常采用电流斩波控制；但在电流斩波控制条件下，系统的研究SRM结构参数对转矩脉动影响的文献并没见报道。因此，本文采用磁路和二维有限元相结合的方法，在电流斩波制条件下，对影响SRM转矩脉动的结构因素进行了分析。

2 SRM的结构及特点

由图1知，SRM由装有励磁绕组的凸极定子和凸极转子组成，转子上无绕组和永磁体，惟一的磁势源来自定子绕组，这是SRM的一个显著优点，由于定、转子的独特的双凸极结构，使SRM结构简单坚固、可靠性高、容错能力强、调速性能优异、适合于高速或者超高速运行。但也由于SRM的双凸极结构，工作原理不同于传统的交流电机，其电磁场分析较复杂，非线性问题严重，存在较大的转矩脉动和噪声。

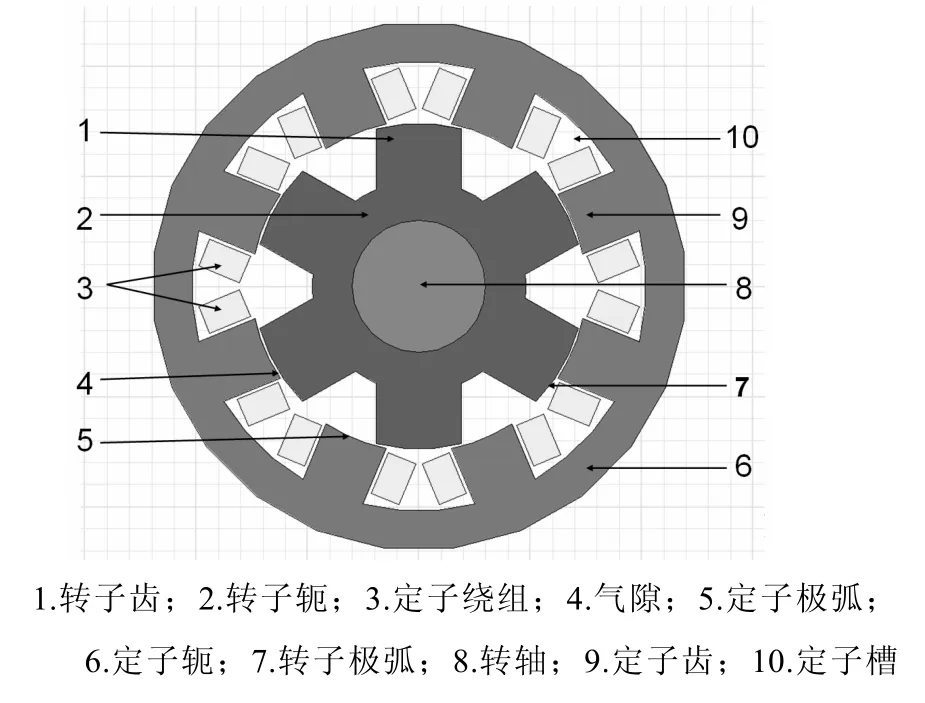
图1 SRM的结构

3 电机磁场的分析计算方法

本文对电机磁场进行有限元计算时，采用矢量磁位进行求解。为了建立磁场的微分方程，确定求解区域和有限元求解的边界条件，假设[6]：

（1）忽略电机端部效应，电机磁场沿轴向均匀分布，即电流密度矢量 J 和矢量磁位A只有轴向分量，J=Jz，A=Az。

（2）铁心冲片材料各向同性，且磁化曲线是单值的，即忽略磁滞效应。

（3）电机机壳外部和转轴磁场忽略不计，即定子外表面圆周和转子内表面圆周为一零矢量位面。

（4）忽略铁心的涡流效应。

从工程角度看，电机的定子外缘可认为是磁场的边界线[7]。因此，磁场的求解模型如图 1所示。用于磁场分析和计算的SRM结构参数如表1所示。开关磁阻电机采用8/6极结构,功率变换器采用全电压型电路（Full-Voltage），SRM工作处于电动状态，定、转子硅钢片采用Steel_1010，迭压系数为0.95。系统仿真时，电流采用斩波（Chopped Current Control，简称：CCC）控制方式，电流上限（Max Current for CCC）设为25A，电流下限（Min Current for CCC）设为0A，开通角设为0度（机械角度，下同），关断角设为22.5度。

表1 SRM结构参数

表2 SRM主要性能数据

4 影响SRM转矩脉动的结构因素分析

4.1 气隙变化对转矩脉动的影响

图2是SRM转矩脉动随气隙长度变化的情况，由图可知，气隙长度在0.10mm到0.50mm之间时随着气隙长度的增大，SRM的转矩脉动逐渐减小，当气隙长度从0.50mm到0.78mm时，转矩脉动反而增大，满足较小转矩脉动得气隙长度，存在一个最优值0.50mm。

由图2可以看出，当气隙长度为0.1mm时SRM的平均转矩并没有比气隙长度为0.5mm时明显高出很多，这是因为，减小气隙长度，SRM的合成气隙磁导相应的的增加，电机的主磁通增加，但是由于主磁通通过铁心齿部存在着高度的局部饱和现象，主磁通的增加会加重铁心的饱和度，使局部铁心的磁导率下降。这使得电机的主磁通并不是随着气隙长度的减小而成比例的增加；同时，定转子之间的漏磁也随着气隙长度的减小而成比例的增加，漏磁对主磁通的影响增强，当气隙长度减小到某一特定值，漏磁对主磁通的影响随气隙长度的变化将变得很小。

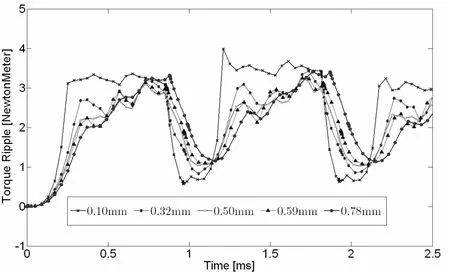
图2 气隙长度对SRM转矩脉动的影响

图3表示气隙长度分别为为0.10mm和0.50mm时SRM的磁化曲线，说明气隙长度较小时，电机的饱和点被提前，电机的带负载的能力有所降低。

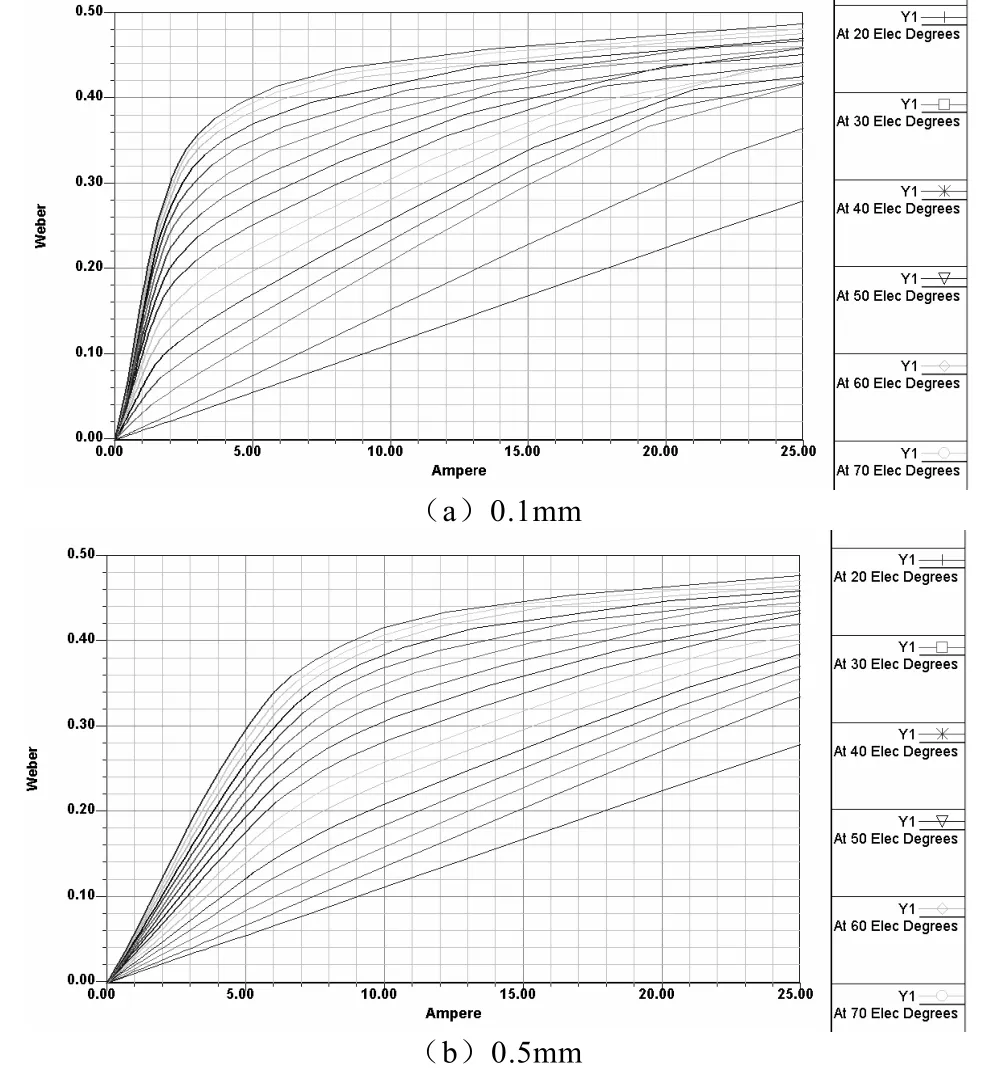
图3 气隙长度分别为0.1mm和0.5mmSRM的磁化曲线

4.2 定、转子极弧系数对SRM转矩脉动的影响

SRM的定、转子齿宽随定、转子极弧系数的变化而变化，定、转子齿宽不同，电机出力的区域不同，进而影响到电机的转矩脉动及平均转矩。

（1）定、转子极弧系数范围的确定

由于SRM属于双凸极结构，其定子和转子极弧的选择对电机的性能有至关重要的作用。定转子极数和极弧的选择应满足[8]：①电机在任何转子位置下都具有正、反方向的自起动能力；②减小不对齐位置时每相绕组的最小电感；③减小各相绕组间的互感；④最小化各相绕组的开关频率。

若保证电机在任何转子位置都具有正、反方向的自起动能力，则要求当某一相定、转子极处于极对极，相邻相定、转子极必须有一定的重叠，也即要求两相邻相电感曲线上升段具有一定的重叠，如图4所示。

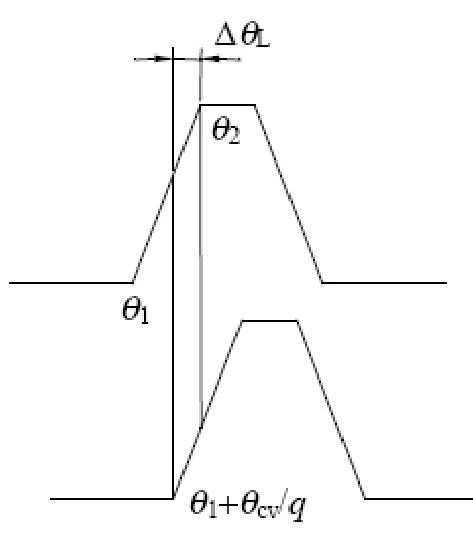
图4 电感重叠角图例

各相矩角特性之间的相位差为θcy/q(q=Ns/2)。故重叠角∆θL为

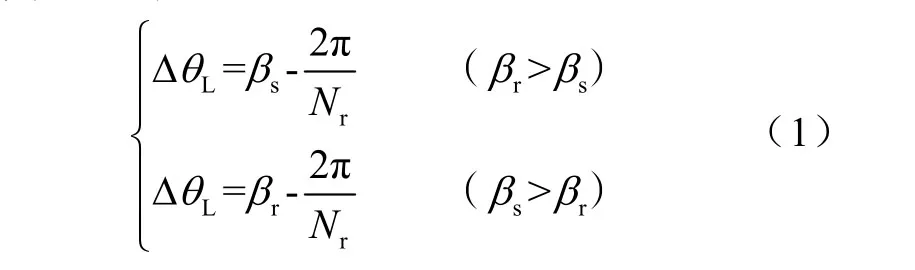
式中，βs为定子磁极极弧；βr为转子磁极极弧。所以极弧满足的必要条件为

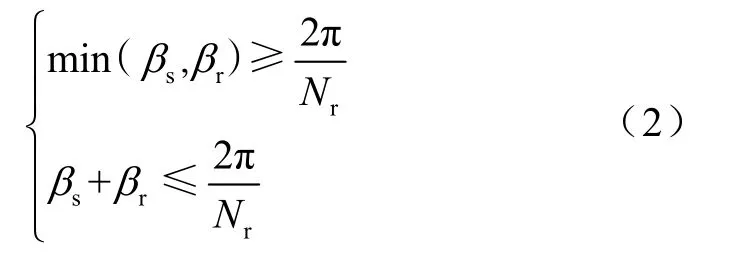
当上式（2）不满足时，SRM 只具有单方向的自启动能力，起动时电机的转向因转子的不同而不同。

为了仿真分析的方便以下采用极弧系数，极弧系数定义为[9]：极弧宽度 bp与极距 τ之比称为极弧系数；以下分析仍以8/6极结构SRM为例，则：定子极距角为45°，转子极距角为60°。

1）定子极弧系数范围的确定

在分析定子极弧系数变化规律时，转子极弧系数的选取对定子分析过程影响不大[10]，选取转子极弧系数为0.50；此时：βr=30°满足（2）式的条件的βs≦30°，假设：βs=30°，得到此时最大定子极弧系数为：αmax=0.67；最小定子极弧系数为：αmin=0.33。

2）转子极弧系数范围的确定

在分析转子极弧系数变化时，定子极弧系数的选取对转子分析的过程影响不大[10]，取定子极弧系数为 0.50，即：βs=22.5°，转子最大极弧系数为αmax=0.625；转子最小极弧系数为：αmin=0.25。

（2）定子极弧系数对转矩脉动的影响

图5是定子极弧系数变化时，得到的SRM转矩脉动变化曲线。

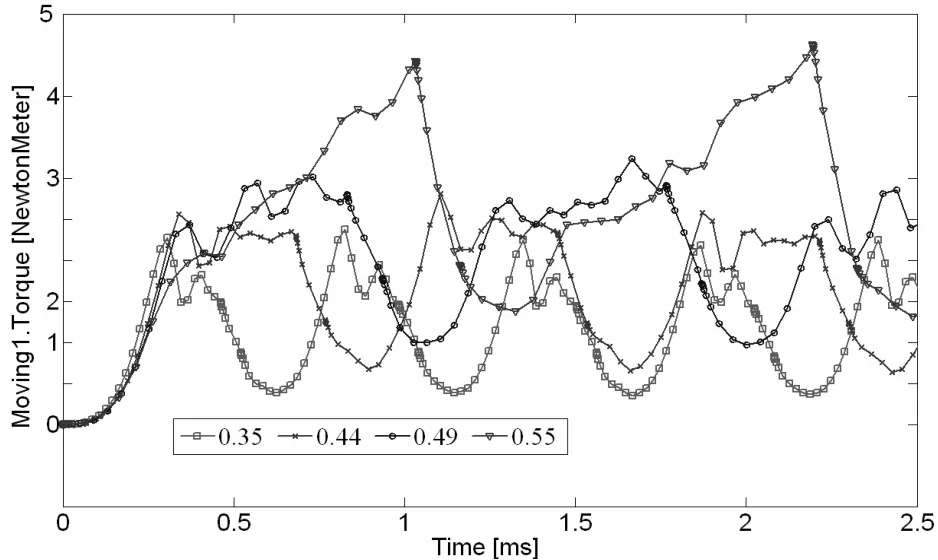
图5 定子极弧系数对转矩脉动的影响

由图5知，随SRM定子极弧系数的增大，平均转矩不断增大，转矩脉动几乎不变，但定子极弧系数大于0.49后，随着平均转矩的增大，转矩脉动大幅度增大；因此，综合考虑电机的转矩脉动和平均转矩，定子极弧系数为0.49左右时电机性能最好。

（3）转子极弧系数对转矩脉动的影响

图6是转子极弧系数变化时，得到的SRM转矩脉动变化曲线。

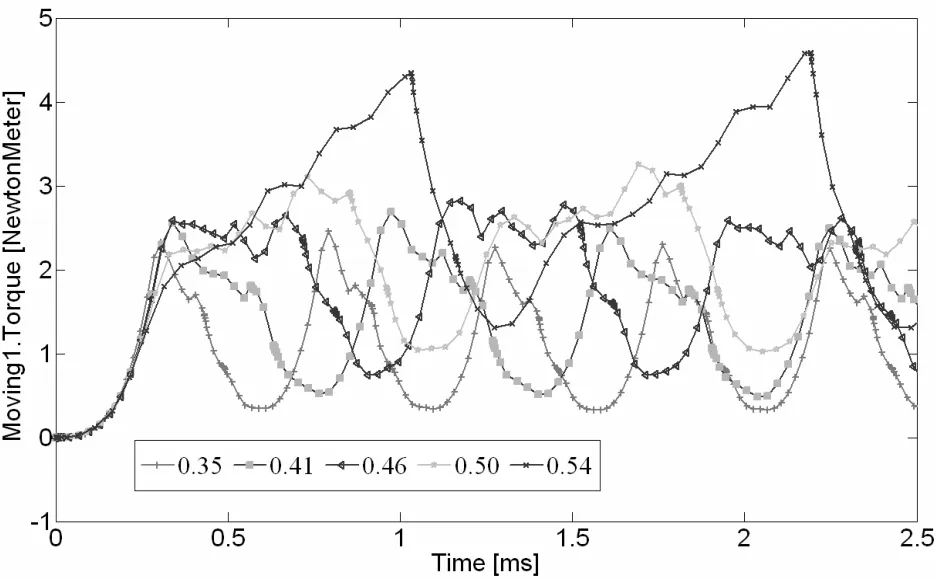
图6 转子极弧系数对转矩脉动的影响

由图6知，转子极弧系数对转矩脉动的影响与定子极弧系数对转矩脉动的影响类似，即随SRM转子极弧系数的增大，平均转矩不断增大，但当定子极弧系数大于0.50时，随着极弧系数的增大，转矩脉动大幅度增大；因此，综合考虑电机的转矩脉动和平均转矩，此时转子极弧系数为0.50左右时电机性能最好。

4.3 定、转子轭厚度对转矩脉动的影响

（1）定子轭厚度对转矩脉动的影响

图7是转矩脉动随定子轭部厚度变化情况，由图知，定子轭部厚度对 SRM 转矩脉动的影响并不大，随着定子轭部厚度增加，SRM转矩脉动呈现减小的趋势，考虑电机的平均转矩，定子轭部厚度为7.0mm左右时性能较优。

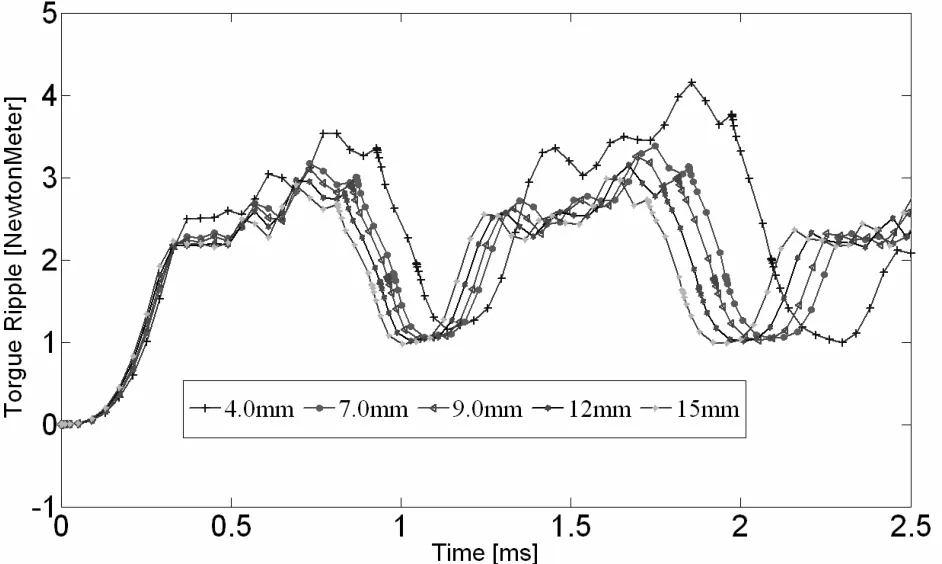
图7 SRM转矩脉动随定子轭部厚度的变化情况

而且由图8磁化曲线知，定子轭部厚度较小时电机的饱和点提前，进而影响电机带负载的能力。当电机定子轭部厚度较大时虽然电机转矩脉动相对较小，带负载的能力得到提高，但是在电机定额给定时，定子轭部厚度增大会导致电机的定子齿变短，电机槽空间变小，增大电机的槽满率，导致电机的损耗增大，降低电机效率，所以在进行电机设计时，不能单一的追求低转矩脉动，而忽略平均转矩和其他性能因素。

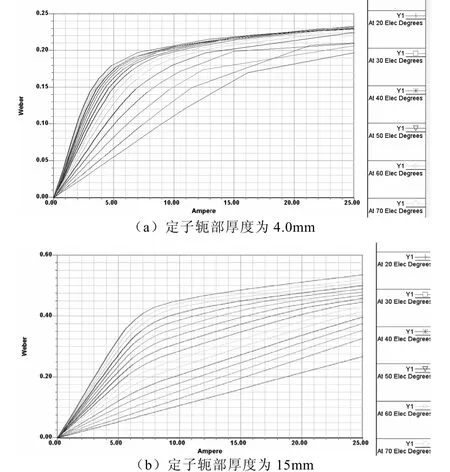
图8 定子轭部厚度分别为4.0mm和15mm时SRM的磁化曲线

（2）转子轭厚度对转矩脉动的影响

SRM定额给定且第一气隙长度固定时，SRM转子轭厚度影响到开关磁阻电机的第二气隙长度，进而影响开关磁阻电机最小电感，影响SRM电感随转子位置角的变化率，影响开关磁阻电机的转矩和转矩脉动；关于SRM第二气隙长度，理论上希望第二气隙长度尽可能大，这样可以获得最小电感，增大电感随转子位置角的变化率，增大开关磁阻电机平均电磁转矩。

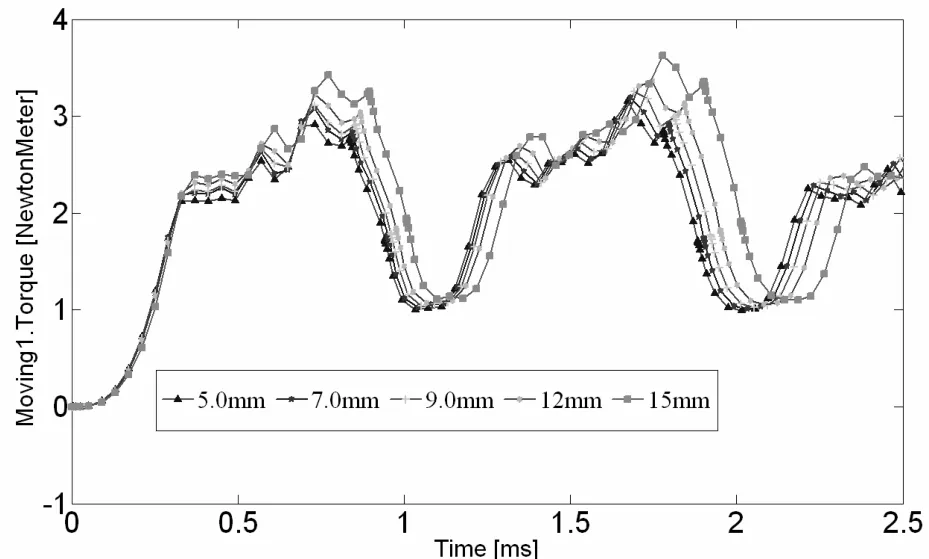
图9 SRM转矩脉动随转子轭部厚度的变化情况

图9是转子轭部厚度变化时SRM转矩脉动的变化情况，由图知，随着转子轭部厚度的增加，开关磁阻电机转矩脉动也随之变大，综合考虑电机的平均转矩和转矩脉动，转子轭部厚度为9.0mm左右时电机性能较优，但总体来说转子轭部厚度对SRM转矩脉动的影响并不大，而且考虑到电机的结构性能和第二气隙长度与转子齿宽的比大到一定程度时，对减小最小电感影响并不大，因此，转子轭部厚度选取要适中。