电力系统潮流分解协调并行计算①

朱永兴，张步涵

(1.中国南方电网东莞供电局，东莞 523000;2.华中科技大学电气与电子工程学院，武汉 430074)

随着三峡电站的并网发电、西电东送工程的实施和全国联网工程的推进，我国将形成规模巨大的超高压、大机组、大电网的全国性互联电网[1]。为了保证互联电网安全稳定运行，迫切需要进行全网一体化仿真计算。传统的串行潮流计算方法在计算速度上已经无法满足大电网模拟和实时控制的仿真要求[2～5]，高性能PC计算机群以其巨大的存储容量和很快的计算速度得到了人们的广泛重视，已成为研究热点。为此，在PC计算机群上快速有效地计算电力系统潮流成了一个新课题[6～8]。

本文通过研究基于节点分割的网络分块法，结合PC机群环境的特性，提出基于网络数学分块的电力系统潮流分解协调算法，在分析原有串行牛顿-拉夫逊法潮流计算数学模型的基础上选取合理的数据元素作为协调变量。并在IEEE14节点和IEEE118节点系统对该算法进行仿真测试。

1 网络分块方法的分类和分割原则

1.1 按切割元素的分类

Kron于20世纪50年代初提出了网络分块计算方法，文献[9]介绍了他所提出的分块法理论。网络分块方法按切割元素主要有两种:一种是支路切割法，即在子网络之间的联络线处加入电流源以代替各子网络之间状态变量的耦合影响，电流源矢量作为该方法的协调变量;另一种是节点分割法，即将原网络分割为子网络后在分割处加入电压源以代替各子网络之间状态变量的耦合影响，电压源矢量作为该方法的协调变量[10]。

1.2 按物理意义的分类

在网络分块法的实际应用过程中，按物理意义又有分为两种:一种为网络的物理分块法，即将整个互联网络人为的强行分割为几个部分，分割之后再通过各个网络的分割处协调变量进行交换迭代，此方法在一定程度上破坏了整个网络的整体性;另一种为网络的数学分块法，此方法其实并不是真正的分割，即形似割而神不割，主要通过将表征网络特性的系数矩阵分解为通过协调部分互连的多个子矩阵，各个子矩阵可独立求解，从而开发潮流求解的并行性。

网络的物理分块方法由于破坏了整个网络的关联性，造成网络的迭代收敛速度变慢，尤其是边界协调部分很慢，更有时若是分割方法不恰当，会造成最后不收敛。而网络的数学分块方法则由于延续了电网的整体性，并没有破坏原始的数学结构，只是尽量开发数学计算上的并行性，因此它的收敛效果和精度与原有串行程序几乎完全一样。但是它的并行度可开发性需要进一步研究。

网络的分块方法和并行算法的基本意义都在于降低潮流计算中雅可比矩阵的阶数以缩短计算时间，当然，并行算法还可以通过其他技术措施来达到缩短计算时间的目的。

1.3 网络分块基本原则

不管是哪一种分块方法都必须遵循以下基本原则[11]。

(1)切割支路或分割节点的规模应尽可能小。因为各个计算节点(处理器)间的必需数据通信量与之息息相关，减少协调变量的数目，可以减少计算节点之间的交互通讯量，降低网络通讯时间对计算速度的影响。

(2)各个子网络规模大小尽量一致，即各个子网络节点数、支路数尽量接近，保证各计算节点的计算负载相对平衡，由于计算时间与导纳元素成比例，所以网络的规模由节点数和支路数共同衡量。

此外，通过并行所获得的效率通常会被由于分块所引起的非零注入元抵消一部分，因此尽量减少非零注入元同样需要被关注。

本文所采用的方法是基于节点分割的网络数学分块方法。

2 分解协调并行计算模型

2.1 线性方程组的分解并行计算模型

首先通过节点优化和因子路径树方法确定网络的分割节点[11，12]，而其他节点则按优化后排序依次排列，分割节点排在节点编号末尾，通过这一步的前期工作。导纳矩阵和雅可比矩阵的系数方程分别变换成

根据潮流计算的功率注入模型分析可知，要着重分析的是雅可比系数矩阵，因为，在利用牛顿-拉夫逊法求解时需要面对的修正方程Ax=b中，A为雅可比矩阵，x为电压修正向量，b为功率偏差值。

经过上面合理的节点优化和分块之后，修正方程转变为对角块加边形式BBDF(bordered block diagonal form)，即

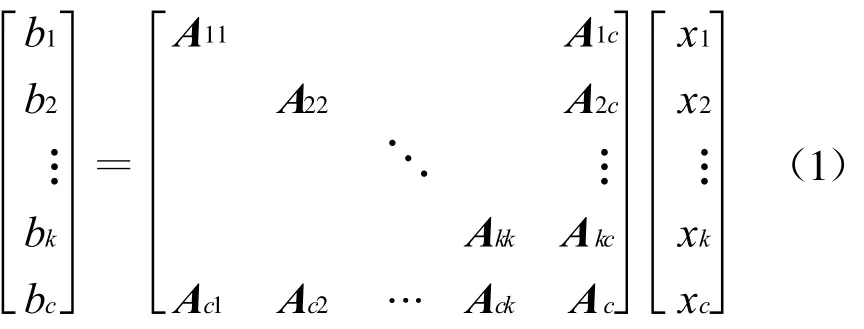
式中:A11，…，Aii是子系统的稀疏矩阵;Ac是协调系统矩阵。

式(1)中第1～k个子系统矩阵块所对应的该行的方程组可以化成形式

而协调块矩阵所对应行的方程组为

消去xi，保留xc得到协调系统方程组为

其中:

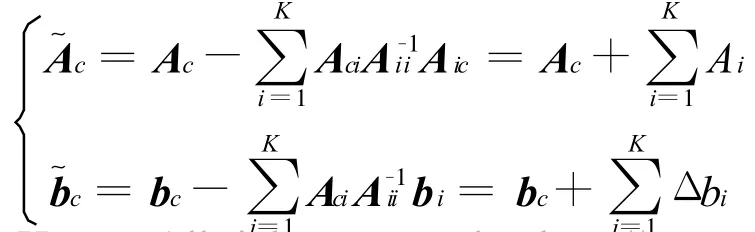
2.2 网络协调与分解

基于BBDF模型的潮流网络分解与协调计算分解图如图1所示。

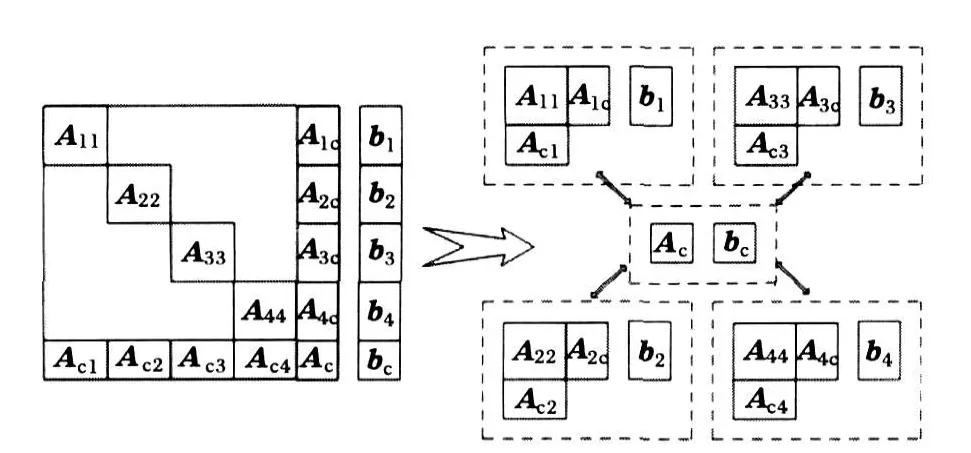
图1 雅可比矩阵分解协调计算任务分配Fig.1 Distribution of Jacobi matrix decomposition and coordination calculation task

每一个子系统的对角元以及下边和右边的边界协调元再加上右端向量被分在一个处理单元，而右下角的边界协调元和它对应的右端向量被分配于协调处理单元。

3 潮流并行算法数学模型和流程

3.1 潮流三角分解协调数学模型

在上一节基础上进一步利用雅可比矩阵的因子表进行网络分块计算。

在每一个子系统(即前面分解图中虚框内的部分)中可以同时进行并行分解计算，即

将式(6)分别代入式(5)中即可得

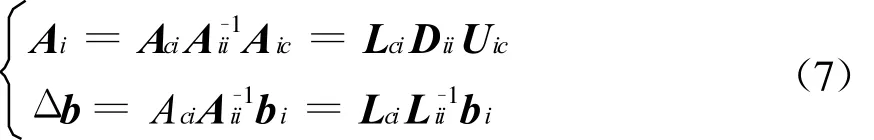
在分解过程中可以用消去法求出 Lii、Dii、Uii、Lci和Uic，并且在消去的同时进行前代运算求出Wi=L-1iibi，即可进行矩阵简单乘法运算求出需要进行通讯的 Ai和 Δ b，其中

考虑到在潮流计算中，修正方程组Ax=b中b向量与雅可比矩阵即A矩阵有一定的关联性，所以需要更进一步的分析。

在直角坐标下，由牛顿-拉夫逊法求解潮流的修正方程式中PQ节点所对应的雅可比矩阵元素和右端向量H 、N、M、L、Δ P 、Δ Q 的表达式可知 :非对角元素仅和节点各自的互导纳以及节点自身电压有关，而对角元素则和节点各自互导纳以及与节点通过支路互连的所有节点电压有关。而右端向量求取表达式中Δ P和ΔQ均同对角元素一样和节点各自互导纳以及与节点通过支路互连的所有节点电压有关。即修正方程雅可比矩阵的对角元素与右端向量通过ai、bi产生联系。其中

所以ai和bi的求取为关键。由于ai和bi与整个网络均有关联难以分割，所以在程序实现时，必须采取一定的策略。

本文所采用的方法是，对于各个子系统(子网络)，一般采取的策略是对于每一个分块加上相应的边界块，在求取该部分导纳矩阵时，直接求取每一行的ai和bi进行单独存储。在每一个分块子系统中，由于任何两个子系统之间无联系(不计及切割节点)，因而ai和bi易于求取。

但是在协调系统(协调网络)中求取则不一样，前面提到ai和bi的值和该行所对应的所有导纳矩阵值以及互连支路上所有节点电压有关，本文的每一个子系统只储存有各自矩阵块和节点电压的信息。而且又发现ai和bi的求取过程是每一个导纳相关值与其对应的电压值相乘后的累加，所以先分开求取ai和bi，然后再进行块的累加求取最终值。即

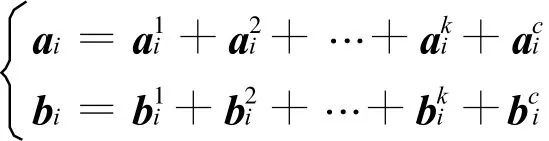
对于PV节点，由于节点电压已知，经过分析可知雅可比元素R、S与右端向量Δ U2没有关联。

通过以上的分析可知，在每个子系统中进行分解计算之后要得到 Ai、Δ bi、aii、bii几个值传送至协调系统。

在协调系统，需要通过输入协调系统的信息获得协调系统雅可比矩阵Ac，通过各个子系统传送来的数据计算 ∑Ai、∑Δ bi和bc，对协调系统方程组式(4)进行分解计算为

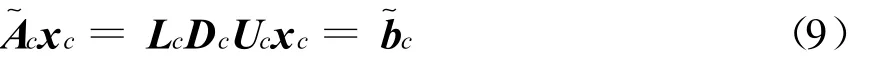
求解xc并将它传送至各个子系统，在各个子系统中同时进行各个xi的求解，即

将式(6)代入式(10)即可求解xi。

通过这一整个过程，即完成一次迭代，判断收敛性即可进入下一次迭代。

3.2 潮流分解计算流程

整个潮流分解计算的流程如图2所示。

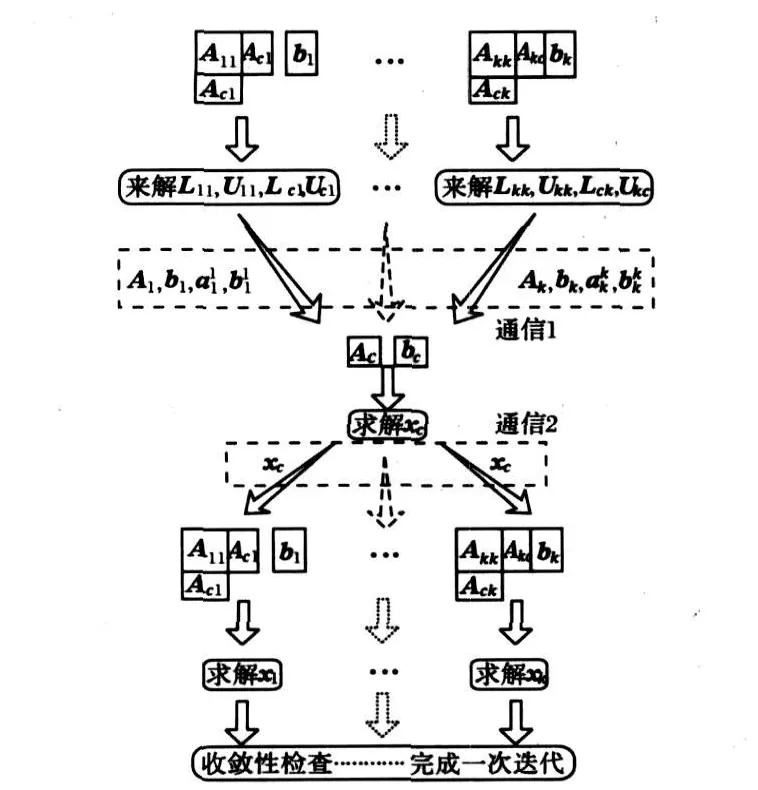
图2 潮流分解协调并行计算流程Fig.2 Process of decomposition and coordination parallel calculation

4 通信

由于通信时间所涉及的技术主要有网络条件、硬件支持以及数学模型这几方面，前面两方面的内容超出本文的研究内容，所以本文在进行并行计算时间统计时暂时不考虑通信时间。

本文所做的只是把数学模型这一部分即需要传输的数据量进行分析，在本文的算法数学模型中，一次迭代所需要的传输数据量与分割节点数目N有关，为(2N+1)2个数据。由于在分割中所选择的分割方案充分考虑了分割节点数尽量小这一关键问题，因此传输数据总量也就相对比较小。

5 算例分析

5.1 测试结果

在时间的测试上，由于网络规模限制，运行时间很短，为了便于比较，本文所测时间都是程序连续运行30次后的时间，时间单位为s。

对于IEEE14节点系统，本文根据合理的分区方案，把标准系统原始节点号为5和9的节点作为分割节点，网络分为上下两个子网来测试运行时间，其测试结果见表1。

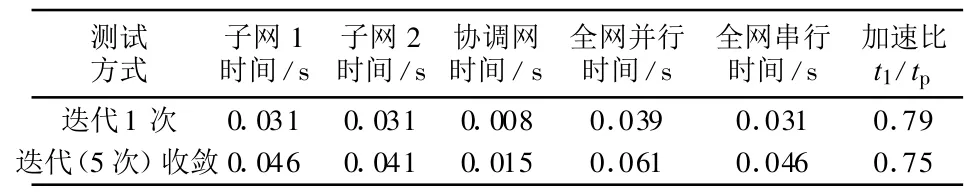
表1 IEEE14节点测试系统参数及结果Tab.1 IEEE14-bus test system parameters and results

对于IEEE118节点系统，根据合理的分区方案，将标准系统原始节点号为 17、19、30 、37、49、65、69、77、80和100的10个节点作为分割节点，将整个网络经过分裂和整合成5个子网，其测试结果见表2。

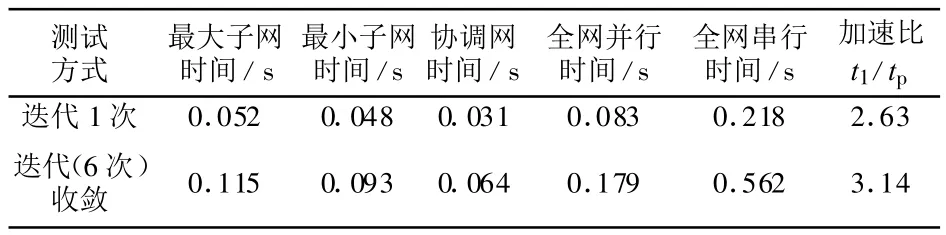
表2 IEEE118测试系统参数及结果Tab.2 IEEE 118-bus test system parameters and results

5.2 结果分析

经过上面的试验测试可以看出，对于IEEE14节点系统，本文所用的并行算法效果并不明显，甚至有时速度会更慢，而对于IEEE118节点系统，可以发现明显的并行效率。

分析以上数据可以做出以下解释，IEEE14节点系统中，由于系统规模小，节点数和支路数也很少，所以在串行程序中能获得很快的速度，而在并行程序中，由于采用分割网络的方法，程序中多了一些分解协调的计算，还有数据的读写也比较费时。但是在IEEE118节电系统中，由于网络的规模已经大到一定程度，完全足以抵消前面所提到的一些多花费的时间，因而取得了可观的加速比。

由此可见，随着网络规模的逐渐扩大，并行程序的加速比将获得提升，并行效率也将增长。

同时还可以发现，协调网所花费时间与其节点规模相比偏大，主要原因在于此程序优化不够，浪费时间多，还有很大的改进空间。

6 结论

本文研究了基于PC机群的电力系统粗粒度并行潮流计算方法，提出了一种适用于PC机群计算环境的基于网络分割的电力系统潮流分解协调并行算法。对IEEE标准系统的测试结果表明，该算法计算精度与普通串行牛顿-拉夫逊法一样高，并且具有客观的加速度。同时，随着网络规模的扩大，加速度将更加明显。

[1] 曾南超(Zeng Nanchao).高压直流输电在我国电网发展中的作用(Role of HVDC transmission in the power system development in China)[J].高电压技术(High Voltage Engineering)，2004 ，30(11):11-12.

[2] 薛巍，舒继武，王心丰，等(Xue Wei，Shu Jiwu，Wang Xinfeng，et al).电力系统潮流并行算法的研究进展(Advance of parallel algorithms for power flow simulation)[J].清华大学学报:自然科学版(Journal of T singhua University:Science and Technology)，2002，42(9):1192-1195.

[3] 张伟，沈沉，卢强(Zhang Wei，Shen Chen，Lu Qiang).电力网格体系初探(一)——电网监控从集中计算到分布处理的发展(Framework of the power grid system part one:Development of power network monitoring from centralized to distributed processing)[J].电力系统自动化(Automation of Electric Power Systems)，2004，28(22):1-4 ，26.

[4] Chan K W，Daniels A R，Dunn R W，et al.Partitioning algorithm for parallel processing of large power systems network equations[C]∥The 2nd International Conference on Advances in Power System Control，Operation and Management，Hong Kong，China:1993.

[5] Tu Feng，Flueck A J.A message-passing distributed-memory parallel power flow algorithm[C]∥IEEEPower Engineering Society T ransmission and Distribution Conference，New York，USA:2002.

[6] 李亚楼，周孝信，吴中习(Li Yalou，Zhou Xiaoxin，Wu Zhongxi).基于PC机群的电力系统机电暂态仿真并行算法(Personal computer cluster based parallel algorithms for power system electromechanical transient stability simulation)[J].电网技术(Power System Technology)，2003 ，27(11):6-12.

[7] 薛巍，舒继武，严剑峰，等(Xue Wei，Shu Jiwu，Yan Jianfeng，et al).基于集群机的大规模电力系统暂态过程并行仿真(Cluster-based parallel simulation for power system transient stability analysis)[J].中国电机工程学报(Proceeding of the CSEE)，2003，23(8):38-43.

[8] 刘学军，刘军(Liu Xuejun，Liu Jun).一种新型的潮流并行计算方法-动态异步并行算法(A new parallel method in power flow calculation-dynamic asynchronous parallel algorithm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，1999，11(5-6):101-106.

[9] Torralba A，Gomez A，Franquelo L G.Three methods for the parallel solution of a large，sparse system of linear equations by multiprocessors[J].International Journal of Energy Systems，1992 ，12(1):1-5.

[10] 张伯明，陈寿孙.高等电力网络分析[M].北京:清华大学出版社，1996.

[11] Chan K W，Dunn R W，Daniels A R.Efficient heuristic partitioning algorithm for parallel processing of large power systems network equations[J].IEE Proceedings:Generation，Transmission and Distribution，1995，142(6):625-630.

[12] 洪潮，沈俊明(Hong Chao，Shen Junming).求解大型稀疏线性方程组的一种并行算法及其在并行潮流计算中的应用(A parallel algorithm for solving large sparse matrix equations and its application to parallel power flow calculation)[J].武汉水利电力大学学报(Journal of Wuhan University of Hydraulic and Electric Engineering)，2000 ，33(4):29-34.