求解动态无功优化问题的解耦算法①

黄 伟，刘明波，赖永生

(1.广东电网公司佛山供电局，佛山 528000;2.华南理工大学电力学院，广州 510640;3.厦门超高压输变电局，厦门 361004)

动态无功优化问题是根据未来一天各负荷母线的有功和无功变化曲线，通过调节并联电容器组的出力及有载调压变压器的分接头，在满足各种约束条件下使整个电网的电能损耗最小。

迄今，已提出多种动态无功优化问题的计算方法。文献[1～5]采用动态规划法或混合法确定在未来一天24小时内安装在馈线上的电容器的投切方案或变电站内的电容器和有载调压变压器的控制方案。由于需要给出未来24小时的控制策略，不得不采用各种方法缩小搜索空间。文献[6]把配电网络分成馈线和主站两部分，先对每条馈线单独用动态规划法求出各电容器的投切序列，再对主站用动态规划法进行一次总的全网优化。文献[7]将配电网络的电压无功控制问题分解为变电站内的电容器和有载调压变压器控制子问题与安装在馈线上的电容器投切子问题，分别用简化的动态规划法和模糊控制算法求解这2个子问题，并提出了协调2个子问题的方法。文献[8]根据网损在各时段的分布，并对对应的负荷曲线进行分段，采用等面积原则把负荷曲线等值成阶跃曲线，并且使阶跃数小于或等于设备的动作次数，从而把动态优化等效成若干个时段的静态优化。文献[9]给出了完整的动态无功优化模型，先通过启发式规则确定并联电容器组及有载调压变压器分接头的动作序列，再简化动态无功优化模型，并将该模型转化为静态优化模型，从而可用常规的优化方法求解。文献[10]提出了配电网无功优化的分时段控制策略，且所分负荷时段总数即为电容器组的最大调节次数。文献[11]将模糊集理论应用于配电网络动态无功优化的建模，并采用模拟退火算法求解。文献[12]提出了一种动态无功优化算法。该算法较好地解决了变量离散化和限制控制设备动作次数之间的配合问题，但随着系统规模的扩大，其计算量会急剧增加，甚至可能会出现数值精度问题。

本文在文献[12]的基础上，提出基于近似牛顿方向的解耦方法，以提高算法的计算效率;并结合一个系统进行验证。

1 动态无功优化模型和其基本算法

设系统有n个节点、u台有载调压变压器、m台发电机，有r个节点装设可投切电容器组。为了方便，设1号节点为平衡节点。将全天等分为24个时段，从而将各负荷母线的全天有功和无功变化曲线分为24段，并认为各时间段中的负荷有功和无功功率保持恒定。于是以系统全天电能损耗最小为目标函数的无功优化模型可以描述为

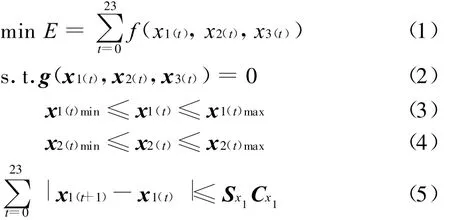
式中:E为全天能量损耗;t=0，1，2，…，23;f(x1(t)，x2(t)，x3(t))为第t时段的有功损耗;g(x1(t)，x2(t)，x3(t))=0为第t时段的节点功率平衡方程，g(x1(t)，x2(t)，x3(t))∈ R(2n);x1(t)为第 t时段的有约束离散控制变量列向量∈R(p)，p=r+u;QC(t)为第t时段可投切电容器组的无功出力列向量，QC(t)∈R(r);TK(t)为第t时段有载调压变压器的变比列向量，TK(t)∈R(u);x2(t)为第t时段的连续有约束变量列向量，x2(t) =∈ R(q)，q=m+n;QG(t)为第t时段发电机的无功出力列向量，QG(t)∈R(m);V(t)为第t时段节点电压幅值列向量，V(t)∈R(n);下标max和min分别表示变量的上限和下限;x3(t)为第t时段的无约束连续变量列向量，x3(t)=[PG1(t)，θ2(t)，θ3(t)，…，θn(t)]T∈R(n);PG1(t)为第t时段平衡发电机有功出力;θi(t)(i=2，3，…，n)为第t时段节点电压相角列向量|表示控制设备(可投切电容器组和有载调压变压器分接头)全天24小时内的动作次数约束列向量;Sx1为控制设备调节步长对角矩阵，其对角元素分别对应于电容器组无功出力和变压器分接头的调节步长，Sx1∈R(p×p);Cx1为控制设备动作次数约束列向量，其元素分别对应于可投切电容器组和有载调压变压器分接头的全天最大允许动作次数MADSON(maximum allowable daily switching operation number)，Cx1∈ R(p)。

采用引入了离散惩罚的非线性内点法求解该模型，最后可得到降阶修正方程为

求解修正方程(6)，可得到原变量和对偶变量的修正方向为 Δ x1(t)、Δ x2(t)、Δ x3(t)、Δy(t)，t=0，1，2，…，23。详细的求解过程参见文献[12]。

可见，算法的计算量主要集中在对修正方程(6)的求解上。随着系统规模的增大，和优化变量的增多，求解所需的计算时间会急剧增长。因此有必要寻求一种有效的方法去解决这个问题。

2 基于近似牛顿方向的解耦算法

2.1 修正方程的解耦形式

为方便讨论，把原问题式(1)～式(5)简写成

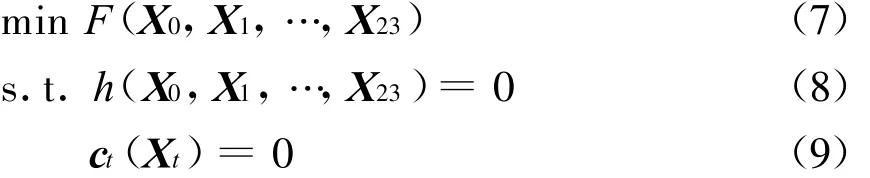
式中:F为目标函数，具有可分离形式;t=0，1，2，…，23;Xi表示第i个时段所有变量构成的列向量;式(9)表示第t时段的所有等式约束方程，不等式约束(3)和(4)可以通过引入松弛变量转化为等式约束;式(8)表示控制设备的动作次数约束方程，对应不等式约束(5)。

可见，由于控制设备的动作次数约束方程(8)的存在，h(X0，X1，…，X23)是 24个时段各变量的函数，这个约束导致修正方程要联立求解[12]。

如果要实现对修正方程的解耦分解，就必须将方程(8)进行分组，其组数N应该小于或等于24。并假定:对于第t组方程，优化变量只有Xt，其余的X1，X2，…，Xt-1，Xt+1 ，…，X23 均为常数 。

根据这一思想，可以把方程(8)展开写成N组方程为

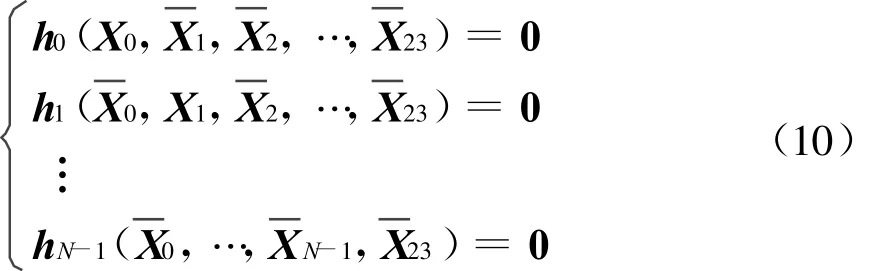
为了讨论问题的简便，此处假定N=24。在方程(10)中，各方程的维数定为

此时，解耦后的动态无功优化模型可写为

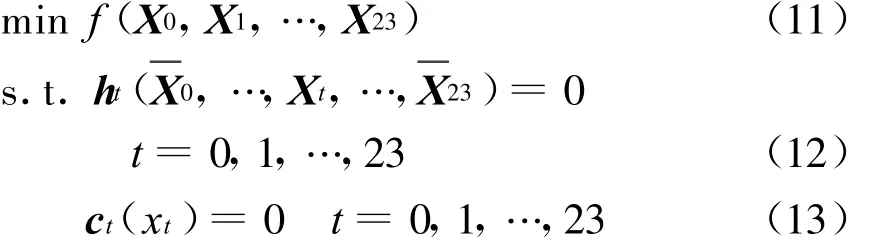
用引入了离散惩罚的非线性内点法求解解耦模型(11)～(13)，得到修正方程为

式(14)还可以进一步写成解耦形式，即

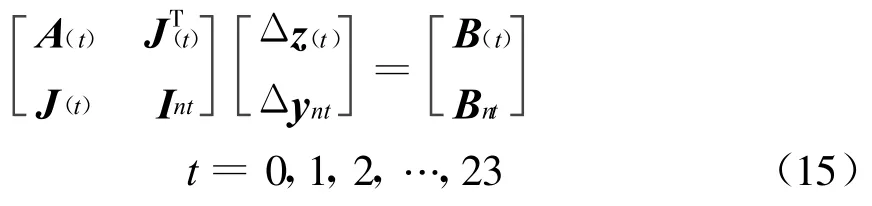
对于N ＜24的情况，同样可以得出类似(15)的修正方程。

式(15)是一个维数比式(6)小很多的方程组，容易求解。

2.2 收敛性分析

按上述方法进行计算，仅仅是完成了一次牛顿迭代求解，得到的只是近似牛顿方向，这并不一定能保证算法的收敛性[13]。

将第k次迭代时得到的修正方程(6)表示为

而采用解耦方法分解后的修正方程表示为

考虑到在不断扩大的系统规模面前，修正方程组(6)的维数也将越来越大，最终可能会在求解过程中引起数值误差。本文以为预处理器，以作为迭代初值，采用求解大型稀疏非对称线性方程组中常用的GMRES算法[14，15]，再次求解修正方程(6)，得到修正方向 Δk。

2.3 计算步骤

综上所述，每一次迭代都可以分为以下步骤完成:

步骤1 形成修正方程(6)，简写为式(16);

步骤2 对离散变量和约束适当分组，将修正方程解耦分解成式(17);

步骤5 用 Δk作为迭代步长，修正各变量，进入下一次迭代过程。

3 算例分析

3.1 试验系统

该系统包括1个220 kV变电站(鹿鸣站)和4个110 kV变电站(景泰站、盘福站、越秀站、文德站)，控制范围从220 kV站进线端到10 kV出线端，如图1所示。220 kV和110 kV母线电压范围限定为1.00～1.07(标幺值，以线路额定电压为基准)。

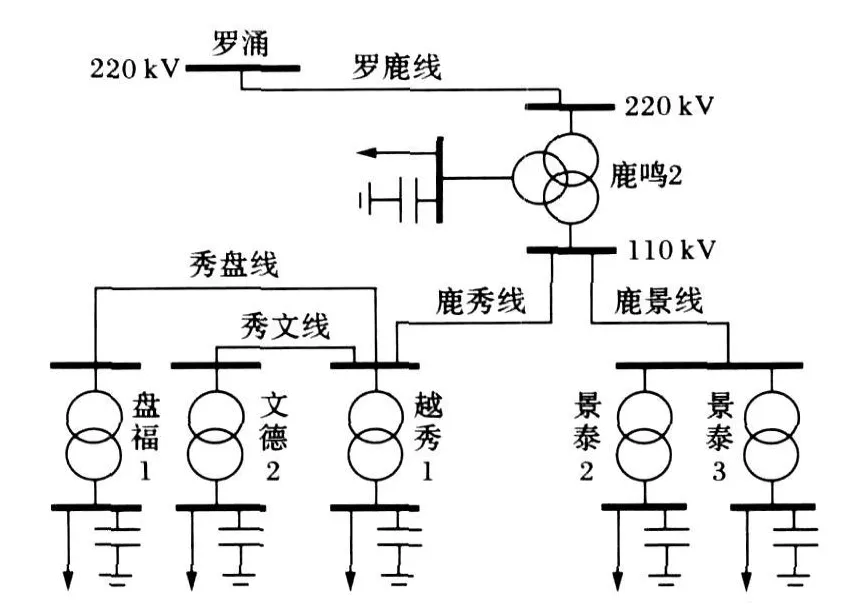
图1 鹿鸣电网正常运行方式接线图Fig.1 Connection diagram of luming electric power network

鹿鸣网正常运行方式下，有6台有载调压变压器参与运行，分别为:鹿鸣 2#变、景泰2#变、景泰3#变、盘福1#变、越秀1#变、文德2#变。变压器档位范围:鹿鸣2#变为(1.03±8×0.015)，其余均为(1±8×0.015)。每台变压器低压侧母线的电压合格范围均为1.00～1.07。所带负荷有6个，每个负荷母线均装设可投切并联电容器组。电容器组配置情况见表1，用标幺值表示。基准功率选定为100 MVA。

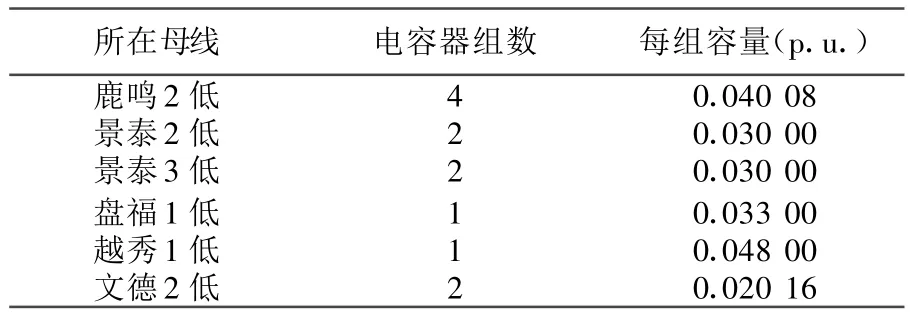
表1 可投切电容器组配置情况Tab.1 Configuration of switchable capacitor banks

以2001年9月10日的24小时负荷数据及网络参数进行计算。本文所用的优化程序用C语言编写，在Visual C++6.0环境编译。所用计算机为Pentium Ⅳ2.8G，内存256 M。

3.2 优化结果分析

为了验证本文提出方法的正确性和可行性，本文对两种方法做了比较:(1)本文提出的解耦分解方法，用方法一表示;(2)文献[12]提出的方法，用方法二表示。表2列出了部分MADSON取值时，由两种优化方法得到的能量损耗、迭代次数和计算时间的比较。

表3和表4分别列出了两种动态无功优化方法变压器分接头动作次数和电容器组投切次数的比较，限于篇幅，这里仅列出了动作次数约束值取11和26的结果。

表2 能量损耗、迭代次数和计算时间比较Tab.2 Comparison of energy loss，number of iteration and execution time

表3 变压器分接头动作次数比较Tab.3 Comparison of transformer tap switching operations

表4 电容器组投切动作次数比较Tab.4 Comparison of capacitor switching operations

从表2可以看到，当动作次数约束较为严格时，方法一的迭代次数增加，这证明方法一的收敛性不如方法二好;但当动作次数约束相对宽松时，方法一的计算时间比方法二短，这证明方法一的计算速度较优，系统规模越大这种优势将会越明显。这为方法二随着系统规模的扩大其计算量急剧增加的缺点提供了一种解决途径。

从表2还可看到，无论MADSON取值如何，方法一和方法二的能量损耗都比较接近，表3和表4的比较也表明了两种方法在限制变压器分接头和电容器组动作次数上取得的效果相当，甚至方法一还略有优势。这些都证明了本文算法的正确性和可行性。

4 结论

本文提出了一种将修正方程分解成若干个独立的子修正方程的动态无功优化解耦算法。这在理论上既解决了动态无功优化中变量离散化的难题，又避免了算法的计算量和所需存储空间随着系统规模的扩大而急剧增大的困境。为求解大规模电力系统动态无功优化问题提供了新的思路。

为了保证解耦分解算法的收敛性，必须对其得到的近似牛顿方向进行修正。考虑到GMRES算法求解大型稀疏非对称线形方程组的有效性，本文提出用GMRES算法对近似牛顿方向进行修正，并证明了修正后的算法能满足收敛性的要求。

以广州鹿鸣电网作为算例分析，取得了较为理想的结果，并与同一系统用文献[12]提出的方法的结果进行了比较分析。对比结果验证了本文算法的正确性和可行性。

[1] Hsu Y Y，Kuo H C.Dispatch of capacitors on distribution system using dynamic programming[J].IEE Proceedings:Generation，T ransmission and Distribution，1993，140(6):433-438.

[2] Lu Feng-Chang，Hsu Yuan-Yin.Fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation[J].IEEE Trans on Power Systems，1997，12(2):681-688.

[3] Hsu Yuan-Yih，Yang Chien-Chuen.Hybrid artificial neural network-dynamic programming approach for feeder capacitor scheduling[J].IEEE T rans on Power Systems，1994，9(2):1069-1075.

[4] Hsu Yuan-Yih，Lu Feng-Chang.Combined artificial neural network-fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation[J].IEEE T rans on Power Systems，1998，13(4):1265-1271.

[5] 张鹏，刘玉田(Zhang Peng，Liu Yutian).配电系统电压控制和无功优化的简化动态规划法(A simplified dynamic programming approach to voltage/var control in distribution systems)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，1999，11(4):49-53.

[6] Liang R H，Cheng C K.Dispatch of main transformer ULTC and capacitors in a distribution system[J].IEEE Trans on Power Delivery，2001，16(4):625-630.

[7] Liu Yutian，Zhang Peng，Qiu Xizhao.Optimal volt/var control in distribution systems[J].International Journal of Electrical Power and Energy Systems，2002，24(4):271-276.

[8] 邓佑满，张伯明，田田(Deng Youman，Zhang Boming，Tian Tian).虚拟负荷法及其在配电网络动态优化中的应用(A fictitious load algorithm and it's applications to distribution network dynamic optimizations)[J].中国电机工程学报(Proceedings of the CSEE)，1996，16(4):241-244.

[9] Deng Youman，Ren Xiaojuan，Zhao Changcheng，et al.A heuristic and algorithmic combined approach for reactive poweroptimization with time-varying load demand in distribution systems[J].IEEE T rans on Power Systems，2002 ，17(4):1068-1072.

[10] Hu Z，Wang X，Chen H，et al.Volt/var control in distribution systems using a time-interval based approach[J].IEE Proceedings-Generation，Transmission and Distribution，2003，150(5):548-554.

[11] Liang Ruey-Hsun，Wang Yung-Shuen.Fuzzy-based reactive power and voltage control in a distribution system[J].IEEE Trans on Power Delivery，2003，18(2):610-618.

[12] 刘明波，朱春明，钱康龄，等(Liu Mingbo，Zhu Chunming，Qian Kangling，et al).计及控制设备动作次数约束的动态无功优化算法(Dynamic reactive-power optimization algorithm incorporating action number constraints of control devices)[J].中国电机工程学报(Proceedings of the CSEE)，2004，24(3):34-40.

[13] Conejo A J，Nogales F J，Prieto F J.A decomposition procedure based on approximate Newton directions[J].Mathematical Programming，2002，93(3):495-515.

[14] Flueck A J，Chiang Hsiao-Dong.Solving the nonlinear power flow equations with an inexact Newton method using GMRES[J].IEEE Trans on Power Systems，1998，13(2):267-273.

[15] 蔡大用，白峰杉.高等数值分析[M].北京:清华大学出版社，1997.