双馈风力发电机低电压穿越转子动态过程分析①

黎 芹，张 兴，杨淑英，谢 震

(合肥工业大学电气与自动化工程学院，合肥 230009)

随着风力发电容量、风电场规模越来越大，当电网出现故障时，风力发电机如果像过去一样与电网解列，而不能像常规能源那样在电网故障的情况下对电网提供频率和电压的支撑，则可能导致严重的连锁反应，对电网的稳定运行造成严重影响。因此，随着风力发电装机容量的不断扩大，具有低电压穿越能力(LVRT)已逐步成为风电场的必然要求[1]。双馈风力发电机为使用最广泛的变速恒频风力发电机之一，且由于其特殊的结构，使得双馈电机的低电压穿越问题成为风力发电低电压穿越技术的研究难点和热点[2～4]。

为了便于风力发电系统低电压穿越技术的研究，目前，已有大量文献对电网发生跌落故障时系统的暂态过程进行了研究[6～10]:为了设计保护策略，文献[6]分析了电网电压跌落时转子过电流现象;文献[7]也从提出保护策略的角度对电网电压跌落时转子侧电压电流进行了相关分析;文献[8]虽然详细的分析了电网电压跌落时双馈电机的瞬态过程，但未对电网电压恢复时的动态过程进行研究。由此可见，已有文献大都是针对各自所提出的低电压保护策略对电网故障时的动态过程进行了相关研究，而鲜有文献对电网电压跌落及电压恢复时的动态过程进行详细分析研究。

本文根据双馈风力发电机的数学模型详细地分析了双馈发电机在电网电压跌落及电网电压在各种不同时刻恢复时的动态响应特性，计算出了电网电压跌落时转子侧电压的瞬时最大值与电压恢复时转子侧电压瞬间的最大值与最小值，并在此分析的基础上给出了相关的仿真波形，从而为低电压穿越保护电路的参数设计及控制策略提供了理论依据。

1 双馈电机的转子电压描述

在双馈电机的等效电路中，若将转子侧参数折算到定子侧，并采用电动机惯例，则双馈电机的电压方程和磁链方程[5]表示为

式中:ω表示电机旋转角速度;v表示电压矢量;i表示电流矢量;Ψ表示磁链矢量;R表示电阻;L表示电感;Lm表示互感;下标r表示转子;s表示定子;p为微分算子。

由式(3)和式(4)可得

式中 ，σ Lr为瞬态电感 ，且 σ Lr=L2m/Ls-Lr。

由式(2)和式(5)可得

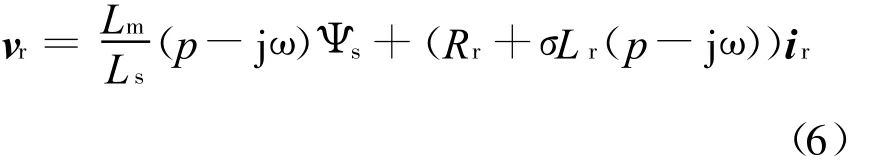
观察式(6)，当转子开路时(ir=0)，转子侧电压为

在电网正常、电机稳态运行情况下，定子电压为一以幅值Vs、同步旋转速度ωs旋转的空间矢量，表达式为

如果定子电阻忽略不计，则由式(1)和式(8)可得

显然，在稳态条件下，定子磁链是一个同步旋转速度旋转的空间矢量，其幅值正比于定子电压。

将式(9)带入式(7)可得

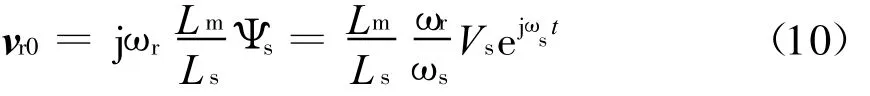
式中 ，ωr=ωs-ω。

另外，转子开路电压vr0的幅值可写成定子电压幅值的函数，即

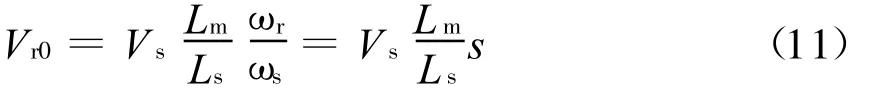
式中 ，s为转差率，s=ωr/ωs。

可见，转子开路电压的大小正比于电机的转差频率。

以上分析了ir=0即转子开路时的转子电压，实际上转子侧电流是由变流器控制的，且运行时ir≠0，因此，由式(6)和式(11)可得变流器控制条件下的转子电压为

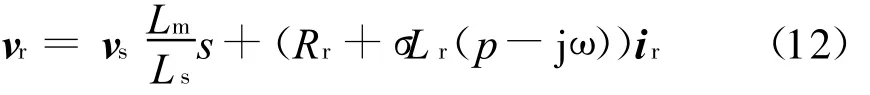
由于转子电阻和瞬态电感(σ Lr)很小，且转子电流频率很低(ω＜10 Hz)，因此转子侧电压vr与vr0的值相差很小[6]。因而在以下的分析中，只考虑转子开路时的情况，忽略由转子电流产生的电压降。

2 电网电压跌落时的双馈电机动态分析

由于电网电压完全跌落即电压跌落至零时，电机将产生最为严重的震荡过程，对系统的危害最大，因此，有必要分析电网电压完全跌落时电机的动态过程。在此假设在t=t0时电网电压发生完全跌落，则双馈电机的定子电压矢量为

由式(1)和式(3)知

解式(14)有

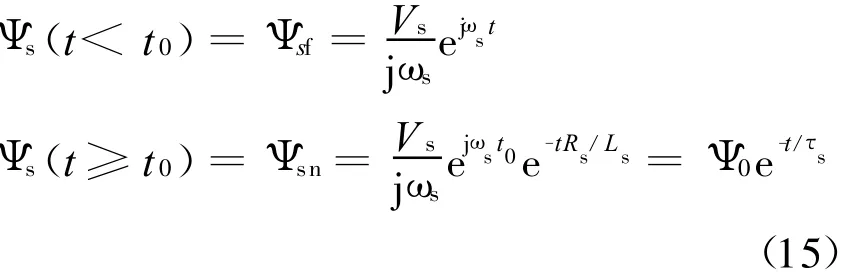
式中:Vs、Ψ0分别为电网电压跌落前的定子电压和磁链 ;τs为定子衰减时间常数，τs=σ Ls/Rs;Ψsf为强制磁链，由系统稳态条件决定;Ψsn为自由磁链，随时间自由衰减。

从式(15)可以看出:当 t＜t0时，定子磁链仅有由电网电压决定的强制分量;当t≥t0时，由式(9)可知，强制磁链正比于电网电压，因此电网电压完全跌落时，这一分量为零，而瞬态分量由自由磁链 Ψsn决定，这一磁链与电网电压无关而只与电机的磁状态有关。自由磁链为当电网电压发生故障时使磁链连续的瞬态分量。因此，当电网电压完全跌落时，定子磁链即为自由磁链，为一瞬态分量。

将式(15)带入式(7)可得电网电压完全跌落时的转子开路电压为

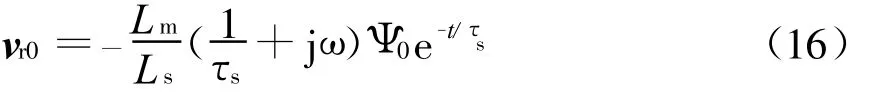
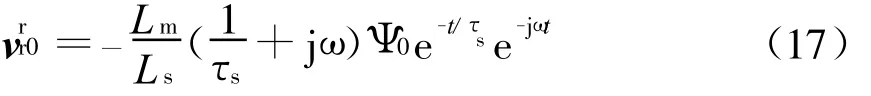
图1给出了当转子转差率为-20%电网电压在t0=1 s时完全跌落时的定子磁链轨迹和转子电压波形。定子磁链自由分量在电网电压跌落时刻以时间常数τs的速度指数衰减，图1(a)为定子磁链的轨迹，图中，采用同步旋转坐标系下的定子磁链定向，因此稳态时的磁链即强制分量为一定值，瞬态分量则为以同步旋转速度旋转的逐步变小的变量。而从式(7)中可以看出定子磁链的变化必将导致转子电压的变化。

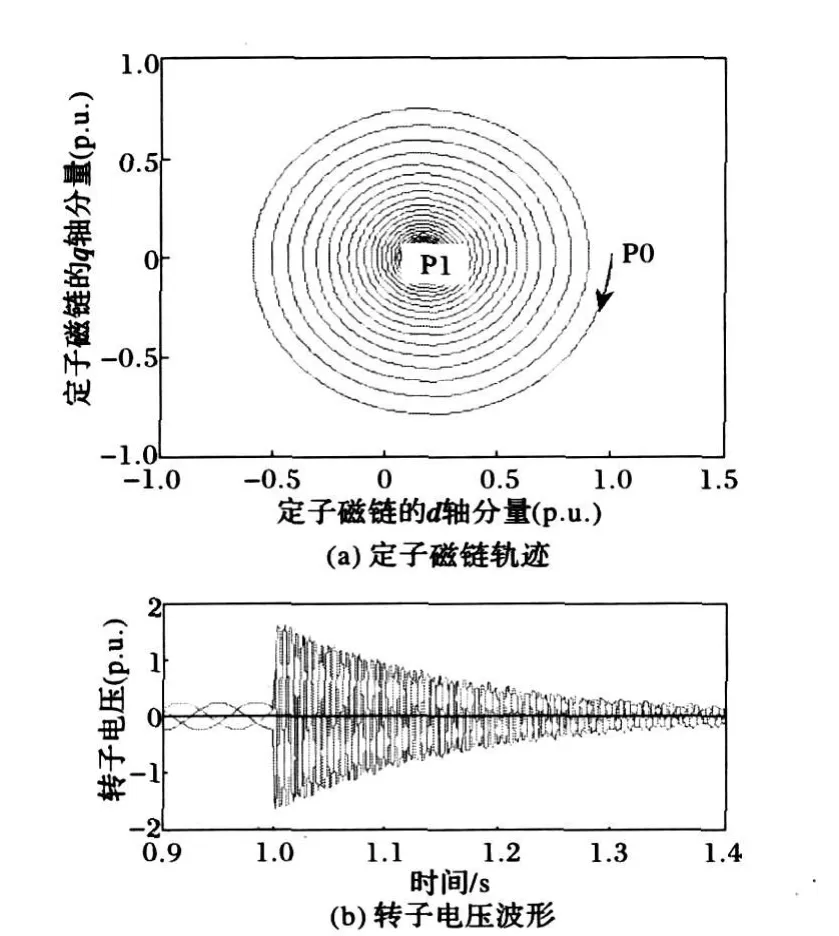
图1 电网电压完全跌落时定子磁链与转子电压波形Fig.1 Waveforms of stator flux and rotor voltages with voltage drop completely

图1(b)为转子电压波形，从图中可以看出，由于定子磁链的震荡转子电压随之发生震荡且在电网电压跌落的第一个周期达到最大值，式(17)中，忽略1/τs项则可得出转子电压的最大值为

从式(18)可以看出当电网电压完全跌落时转子电压的最大值约为正常稳定运行时定子电压的(1-s)倍，而电机转差率一般限制在-0.2～0.2之间，所以当电网电压发生完全跌落时，转子侧的瞬态电压最大可达到定子电压的1.2倍左右。且电机超同步运行时瞬态电压值大于次同步运行状态。而双馈电机正常稳态运行时，转子侧是连有变流器时，则转子侧电压为

在转子旋转坐标系下，则转子电压可表示为

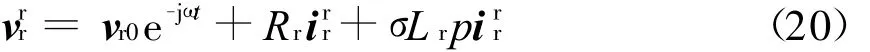
图2给出了转子侧的等效电路，当转子由变流器控制时，由于变流器的容量的限制和直流电容的支撑作用，转子变流器侧的电压不能发生突变，而又由于转子电阻Rr和瞬态电感σ Lr很小，则转子侧电流将会很大。因此如果想限制转子侧电流在允许的范围内，则需要附加其他的保护电路。

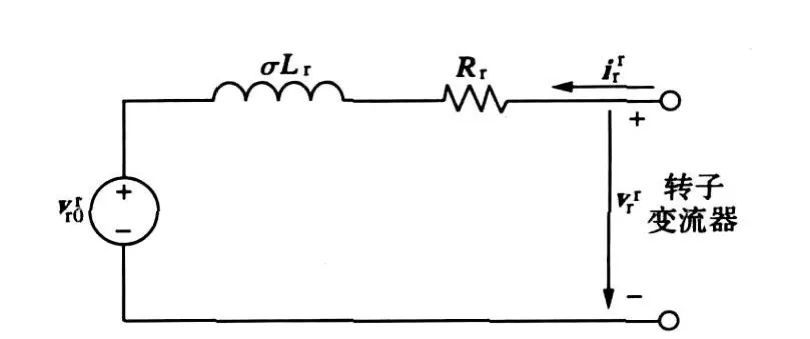
图2 电机转子侧等效电路Fig.2 Equivalent circuit of motor model from the rotor side

3 电网电压恢复时的双馈电机动态分析

前面讨论了当电网电压发生跌落时电机的动态过程，从图1可以看出，定子磁链在动态过程中是以半径逐渐缩小的圆形轨迹渐近于在低电压条件下的新的平衡点的，若电网电压恢复时刻，电网电压跌落时所激起的电磁振荡过程还没有结束，则新的振荡过程将会叠加在前一振荡过程之上。假设在时刻电网电压恢复，即有定子电压

与电网电压跌落不同的是电网电压恢复时刻不确定，这样定子磁链的初始值不确定，式(14)的解为

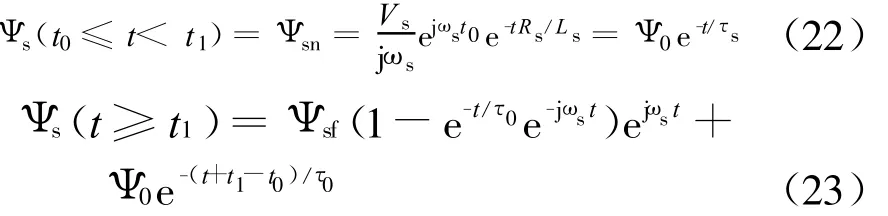
式(23)可改写为

为了方便研究，将磁链表达式放在同步旋转坐标系下研究，在同步旋转坐标系下，则固有磁链为一直流定值，而瞬态直流量则为以同步旋转速度旋转的空间旋转矢量，式(24)可改写为

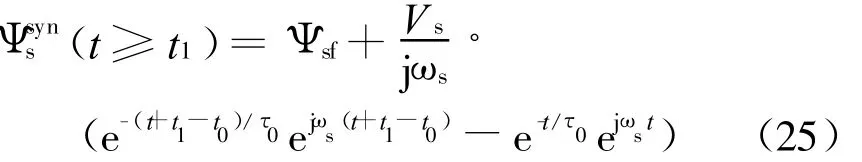
从上式中可以看出，随着电网电压恢复时刻的不同，定子磁链的震荡过程存在以下几种极限情况。

情况一:当 t1-t0=Ts/2(Ts=2π/ωs)时，电网电压恢复时刻的定子磁链震荡幅值最大，即

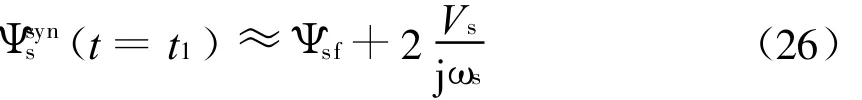
情况二:当t1-t0=Ts时，电网电压恢复时刻的定子磁链震荡幅值最小，即

情况三:而当t1-t0时间足够长即电网电压恢复时定子磁链震荡过程已结束时，定子磁链震荡幅值为

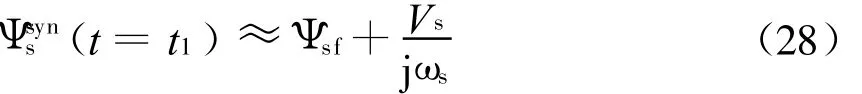
从以上式子可以得出，不同的电网电压恢复时间所引起的定子磁链的震荡将会有很大的差别。

图3给出了在同步旋转坐标系下，电网电压恢复3种不同时刻的定子磁链仿真波形。图中，P0为在额定电压下双馈电机定子磁链的稳态平衡工作点，P1为电压跌落后双馈电机定子磁链在新定子电压下新的稳态平衡工作点。在电网电压跌落时，双馈电机定子磁链将由平衡工作点P0沿方向d1向平衡工作点P1过渡。

图3(a)为情况一(t1=1.01 s)下的定子磁链轨迹，此时定子磁链恰好离平衡工作点P0最远，定子磁链将沿图3(a)中d2的方向向平衡工作点P0收敛，此时电压跌落与恢复时引起的的两个瞬态磁链相加，磁链震荡最为严重;图3(b)给出了情况二(t1=1.02 s)时的定子磁链轨迹图，此时定子磁链恰好离平衡工作点P0最近，这时磁链将沿图3(b)中d2的方向较快地向平衡状态P0点收敛，此时电压跌落与恢复时的两个瞬态磁链相减，磁链几乎不发生震荡，很快进入稳态。而图 3(c)为情况三(t1=1.6 s)时的定子磁链轨迹图，此时在电网电压恢复时双馈电机的定子磁链已处于新的平衡工作点P1处，那么在故障故障切除时，定子磁链将由P1点沿方向d2向平衡工作点P0过渡。

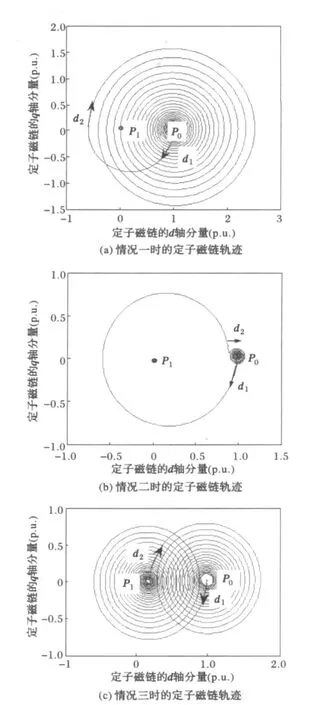
图3 定子磁链轨迹Fig.3 Stator flux trajectory

将式(24)代入式(7)，并忽略与1/τs相乘项，有转子开路时转子电压为

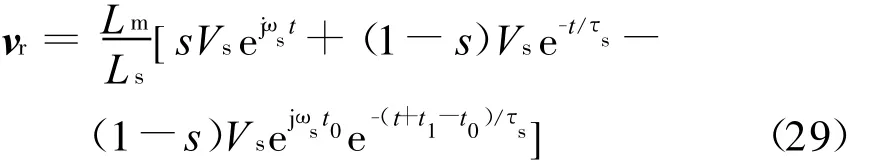
同样，将转子电压也转换到以同步旋转坐标系为参考的坐标系下研究，则式(29)可表示为

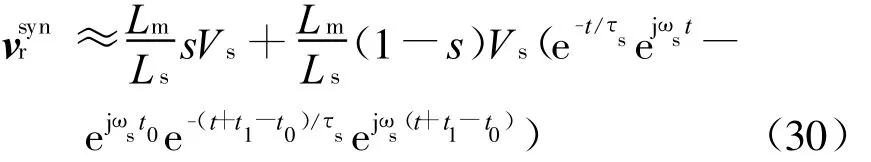
由式(7)可知，由于电网电压不同的恢复时刻对定子磁链的影响不同，因而对转子电压的影响也不同，在上述情况一时，由于定子磁链震荡最严重，则此时的转子电压瞬时值也将最大，由式(30)可得其值为

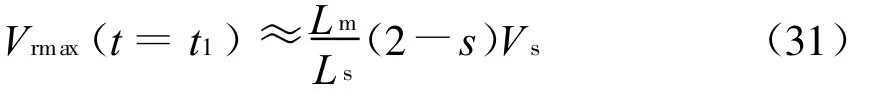
情况二时，由于定子磁链震荡最小，则此时的转子电压瞬时值也是最小的，同样由式(30)可得其值为

而情况三时，定子磁链震荡过程与电网电压跌落时的震荡过程类似，由式(30)有

图4分别给出了电网电压在3种不同情况下的转子电压仿真波形。

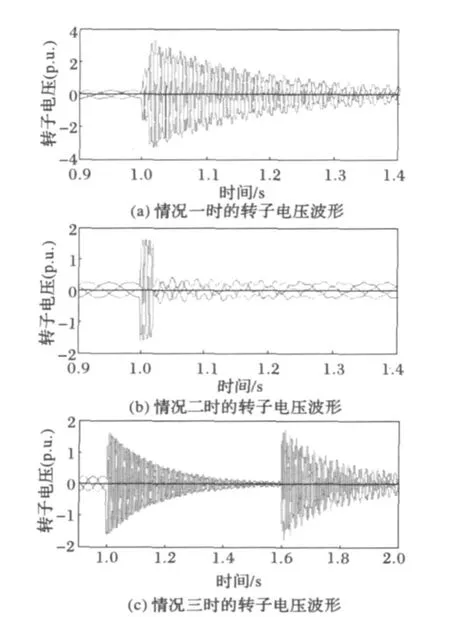
图4 转子电压波形Fig.4 Rotor votage waveforms

从以上分析可知，电网电压恢复时刻对系统的震荡过程影响很大，因此在采用低电压穿越转子保护策略时，对保护电路的参数设计和保护电路的切除时刻都应考虑到电网电压不同恢复时刻的情况。

4 结语

本文对当电网电压完全跌落和电网电压恢复时的双馈电机的动态过程进行了详细的理论分析，在电网电压跌落时，由强制分量引起的转子电压的大小正比于电机的转差率，而由自由分量引起的转子电压的大小与定子电压相当;当电网电压恢复时，不同的恢复时刻所引起的电机的电磁震荡过程不同，对系统的影响也不同。从文中的理论分析和仿真结果可以得到如下结论:

(1)电机正常运行时，转子侧电压为定子侧电压的转差率倍;

(2)电网电压完全跌落时，转子侧电压与电网电压相近;

(3)电网电压跌落时，电机在超同步运行状态比次同步运行状态激起的转子侧电压大，且转速越高，电机动态过程越严重;

(4)电网电压恢复的时刻不同，所激起的电机的震荡大小也不同，最大可达跌落时的两倍。

[1] IEEE P1547.IEEE standard for distributed resources interconnection with electric power systems[S].

[2] Xiang Dawei，Ran Li，Tavner P J，et al.Control of a doubly fed induction generator in a wind turbine during grid fault ride-through[J].IEEE Trans on Energy Conversion，2006，21(3):652-662.

[3] Petersson A.Analy sis，Modeling and Control of Doubly-fed Induction Generators for Wind Turbines[D].Goteborg，Sweden:Department of Energy and Environment，Chalmers University of Technology，2005.

[4] Abbey C，Wei Li，Owatta L，et al.Power electronic converter control techniques for improved low voltage ride through performance in WTGs[C]∥37th IEEE Power Electronics Specialists Conference，Jeju，Korea:2006.

[5] 张开明(Zhang Kaiming).基于PSCAD/EM TDC变速恒频风电机组控制系统仿真(Simulation of the variable-speed constant-frequency wind turbine control system based on PSCAD/EM TDC)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2008，20(3):70-76.

[6] Ekanayake J B，Holdsworth L，Wu Xueguang，et al.Dynamic modeling of doubly fed induction generator wind turbines[J].IEEE T rans on Power Sys-tems，2003，18(2):803-809.

[7] Thiringer T，Petersson A，Petru T.Grid disturbance response of wind turbines equipped with induction generator and doubly-fed induction generator[C]∥IEEE Power Engineering Society General Meeting，Toronto，Canada:2003.

[8] Lopez J，Sanchis P，Roboam X，et al.Dynamic behavior of the doubly fed induction generator during three-phase voltage dips[J].IEEE Trans on Energy Conversion，2007，22(3):709-717.

[9] He Yikang，Hu Jiabing，Zhao Rende.M odeling and control of wind-turbine used DFIG under network fault conditions[C]∥Eighth International Conference on Electrical Machines and Systems，Nanjing，China:2005.

[10]M orren J，de Hann S W H.Short-circuit current ofwind turbines with doubly fed induction generator[J].IEEE T rans on Energy Conversion ，2007 ，22(1):174-180.

[11] Vicatos M S，Tegopoulos J A.Transient state analysis of doubly-fed induction generator under three phase short circuit[J].IEEE Trans on Energy Conversion，1991，6(1):62-68.