小波-LMBP网络在短期负荷预测中的研究与应用①

胡 力，何怡刚

(湖南大学电气与信息工程学院，长沙 410012)

随着电力市场的发展，提高短期负荷预测的精度对于电力系统安全经济运行具有十分重要的意义。传统的预测方法如常规的时间序列法和回归分析法，属于智能原理的神经网络法、专家系统法、模糊逻辑法等都比较成熟，并广泛应用于电力系统运行过程中。但社会经济的发展促使负荷预测的精度要求越来越高，而这些方法在面对非线性与时变性趋势愈来愈明显的负荷预测时往往显得力不从心，因此，寻找更能体现历史负荷与环境因素影响的新型智能负荷预测方法尤为迫切。

本文提出并分析了一种基于小波变换结合LMBP神经网络的电力系统短期负荷预测方法。通过小波变换对负荷序列进行多尺度分析，得到具有不同特征和规律的频段子序列，再对这些子序列分别采用合适的人工神经网络模型进行训练预测，最后将各预测子序列进行重构生成负荷序列的最终预测结果，并给出相应的实例验证。

1 小波分析与LMBP网络简介

小波分析在时域和频域上同时具有良好的局部化性质[1]。小波变换能将各种交织在一起的不同频率组成的混合信号分解成不同频带上的块信号。通过对电力负荷序列进行小波变换可以将负荷序列分别投影到不同的尺度上，而各尺度可近似地看作各个不同的“频带”，这样各尺度上的子序列分别代表了原序列中不同频域的分量，它们更加清楚地表现了负荷序列的特性。

BP网络即误差反向传播网络，是利用非线性可微分函数进行权值训练的多层网络，它包含了神经网络理论中最为精华的部分，其结构简单、可塑性强，在函数逼近等领域广泛应用。

本文采用改进型 LMBP算法，可以提高神经网络训练的收敛速度，降低网络对于误差曲面局部细节的敏感性，有效地抑制网络陷入局部极小。

2 小波分析-LMBP神经网络预测建模

小波分析-LMBP神经网络预测方法分为4个步骤[5，6]:

(1)选择合适的小波函数及分解尺度;

(2)对负荷序列进行小波分解;

(3)采用LMBP神经网络分别对各尺度域上的小波序列进行建模和预测;

(4)将各子序列的预报数据进行小波重构，生成负荷序列的最终预报数据。

构出图形不一定就有解题思路，因此，需要思考作图的合理性，是否满足所有条件；基于构图分解或组合条件思考能得到什么，即定的量与定的关系；将构图所知与问题须知相结合，寻找解题思路.以本题为例，关键检查所构造的点B是否满足AB=AC，∠ABD=30°？分析构图过程，发现满足条件；从构图就点B满足的条件进行思考，发现△ADE为等边三角形，即∠DAE=60°，BE=AE，思考CD=AD与AC=AB又能得到什么？△ADC与△ABE全等；基于构图分析问题求∠ACB的度数，由于AC=AB，于是只要确定∠BAC的度数，将已知与须知知进行对接，就是确定∠BAE的度数，由全等易证.

整个模型结构如图1所示。

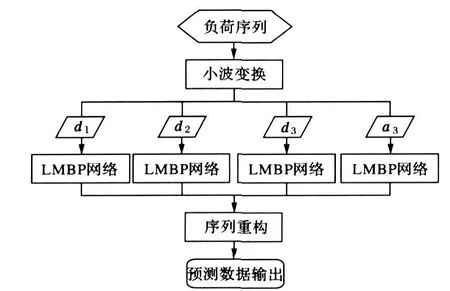
图1 整个预测模型架构Fig.1 Framework of the whole forecasting model

3 小波分析

3.1 小波函数及分解尺度选择

母小波应根据负荷序列的特点进行选择，同时还需要通过构造不同小波基对负荷序列进行分解并对变换结果进行比较，选取最能体现各子序列规律的母小波[3～5]，文中选择四阶 Daubechies函数db4为母小波。同时在一定的预测要求下，分解尺度如果选择太小，则不能有效地将原信号中具有不同的频率特征的分量分离出来;而太大的话则需要用较多的模型对分解后的各分量进行预测，各个模型都会引入一定的误差，从而导致最终预测误差变大[4]。在通过大量数据进行多次分析之后本文选择3尺度对负荷序列进行分解。

3.2 实例数据的小波变换

以某地区2007-06-01-2007-06-30共30天的实测负荷数据作为原始采样数据，每天每隔15 min一个采样点，共30×96=2 880个数据，经过预处理和归一化后按照第3.1节给出的小波分解模型进行小波分析。在分解过程中，由于采用的序列是有限序列，在小波变换进行卷积运算时需要延拓边界，本例中采用周期延拓方式。图2是原始负荷序列s和 3尺度小波分解所得到的d1、d2、d3、a3子序列波形。其中a3是原始序列的低频部分，也称近似部分，从其波形图可以看出曲线比较光滑，基本保持了原负荷序列的形状，并具有明显的日周期性;d1、d2和d3分别为序列在各尺度下的高频部分，也称细节部分，它们隐藏了原始负荷序列的细节特征，其中d1这个尺度 ——高频分量主要表现为随机特征。

图2 原始序列s及小波变换后子序列波形Fig.2 Original sequence and its subsequences after wavelet decomposing

3.3 各尺度域预测模型选择和构建

由于各尺度上的分解序列有其各自的特点，因此应根据不同尺度上负荷变化的趋势分别建立相应的子序列预测模型，可提高最终的负荷预测精度。例如可以对周期性较强的的子负荷序列采用传统的周期自回归法预测，而对波动性较大、周期性不强的子负荷序列采用神经网络法进行预测。本文对所有子序列都采用改进型算法的LMBP神经网络进行预测建模。

LMBP神经网络可对任意一连续函数实现单隐层的网络逼近，因此本文中的LMBP网络采用简单实用的三层结构。在实际应用中，具体到短期电力负荷预测来说，输入变量应该选择与被预测负荷密切相关的数据，包括历史负荷数据和日类型、天气等其他量化数据。当然也并非输入数据越多越好，这不仅与网络规模和运算效率构成矛盾有关，也与难以定量化分析的数据会导致预测效果反而变差的情况有关。在本例中，考虑到预测日之前相当一段时间内的负荷数据基本反映了这段时期内的天气情况，所以仅采用历史负荷数据，暂不计入其他定量化影响因素数据。另外隐层神经元的数目选择也是一个特别重要而又复杂的问题，往往需要根据设计者的经验和多次实验来确定，选择最佳隐单元的参考公式[2]为

式中:i为输入单元数;j为输出单元数;k为[1，10]之间的常数。

其次，如果对所有子序列应用同一LMBP网络进行预测，其效果并不理想，某些序列的预测过程甚至会出现无法收敛的情况。因此对于不同的子序列，其LMBP结构模型也应选择最佳模型，具体到本算例来说，各ANN模型区别就是隐单元个数以及传递函数选择的差异。

输出层的输出为待预测的负荷数据，大都选择以下两种方案[12，13]:

方案2 基于“移动时间窗口”方法，即不是一次把未来24小时的负荷值全都预测出来，而是基于提前1点的预测，以预测值为输入，递推预测出未来24小时的负荷。

在本实例中，两种方案都做过测试，对于方案1，尽管有不少文献仿真表明其可以实现，但多数是在日负荷预测输出点相对较少的基础上采用，具体到本例中，要预测一天96个时刻的负荷，那将有96个输出神经元，隐层单元也相应增多，这对系统的开销造成极大的压力，需要高性能的计算硬件设备，且实验表明其结果并不十分理想。方案2是多数短期负荷预测模型采用的输出方式，具有结构简单，所需系统性能要求低等特点，但这种方案也有一个很大的不足，即在实际预测时一般要在前一个工作日t时之前完成所有预测，显然某些待预测时间点之前是没有实际数据的，只有将此刻前的预测值作为此时间点的预测输入，这样无疑累积了预测误差，预测精度将受到一定影响。

在本实例中采用一种新的输入处理方法，即是将一天的负荷序列分为4段(6 h)×24预测。之所以采用这样一种方式，是因为有文献表明，在一天中的几个时间段内负荷模型会表现出不同的特征，不同时间段负荷所具有的不同变化规律，把一天96点的预测分解为几个时间段子模型来预测其精度不会下降，更重要的是由于每个子网络的规模较小，所以对网络的训练比大规模多输出的网络训练更加容易，相当程度上简化了ANN的结构。图3即是子序列时间分段预测模型。

具体到小波-LMBP网络预测模型来说，由于小波3尺度分解得到4个子序列，分别进行分段预测的话，实际上需要构建4×4个LMBP网络。子序列各自的预测网络应根据该序列自身特点分别建模;子序列尽管分成4个时间段，但整个序列所包含的规律特征连续分布，所以各时间段可以采取完全相同LMBP模型。表1即为各子序列LMBP网络模型参数设置。

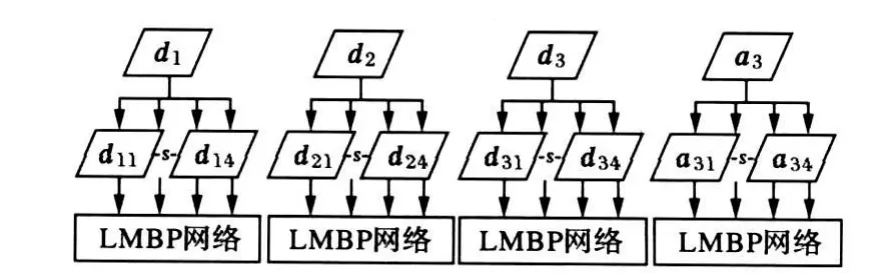
图3 子序列时间分段预测模型Fig.3 Forecasting model of sub-sequences with time division

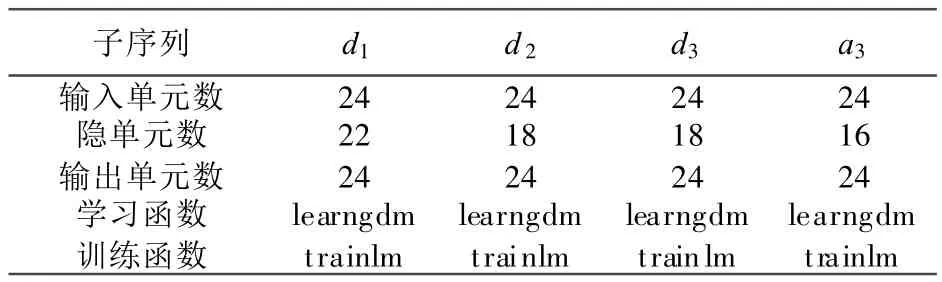
表1 各子序列LMBP网络模型主要参数设置Tab.1 LMBP parameters for four subsequences

4 算例分析

4.1 负荷数据分解及分别预测

以某地2007-06-01-2007-06-28实测的日负荷数据作为训练样本，共28×96个数据，预测该地区2007-06-30的日负荷数据，运用Matlab工具进行实例分析。以小波分解后得到的a3序列为例，图4表明a3子序列LMBP网络通过16次训练后，达到误差要求，其分段序列通过三层24-16-24的LMBP网络预测结果如图5和图6所示。

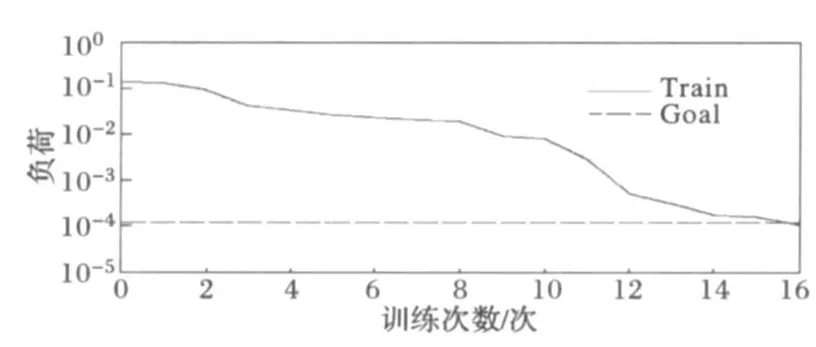
图4 LMBP网络训练结果Fig.4 Trainning results of LMBP

图5 a3序列的第一个分时段预测结果Fig.5 Forecasting result of a3sequence of the first time-period

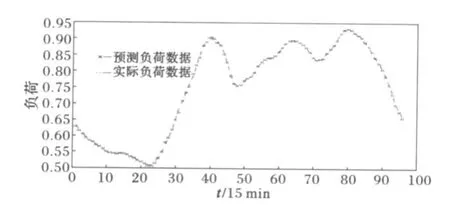
图6 整个a3序列的预测结果Fig.6 Forecasting result of a3

从图5和图6可知，经过小波分解后得到的子序列由LMBP网络预测能得到惊喜的预测精度，这尤其表现在决定预测数据基本走势的低频分量a3上。另外需要说明的是，在其他高频分量的预测实例分析中，得到的预测精度与a3相比稍有差距，这与高频分量决定负荷细节部分且其随机性复杂性相对较强的本质有关。

4.2 预测序列重构

采用上文所述模型进行负荷预测时，其子序列的重构十分简单，即是把各子序列分量在时域上累加，然后进行去归一化处理，可得最终需要的预测日96个时刻数据。图7即为某地区2007-06-30全天96个预测点负荷数据与真实值对比波形。

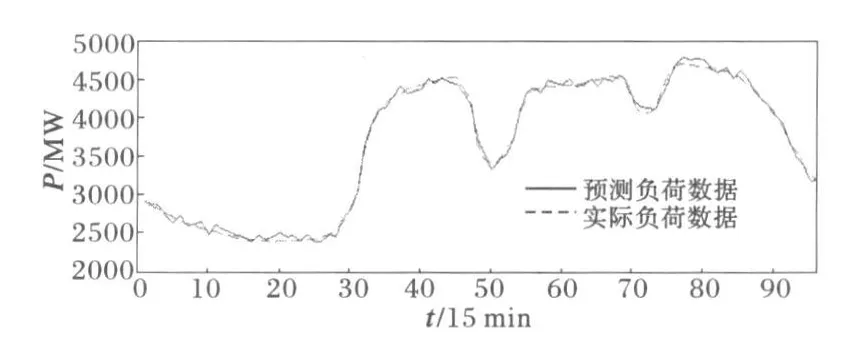
图7 全天96点预测结果曲线Fig.7 Forecasting curves of 96 points in one day

相对误差分布如图8所示，表2为误差统计情况，由此可见，采用小波分析-LMBP网络模型进行日周期负荷预测的精度比较理想，平均相对误差仅有1%左右。

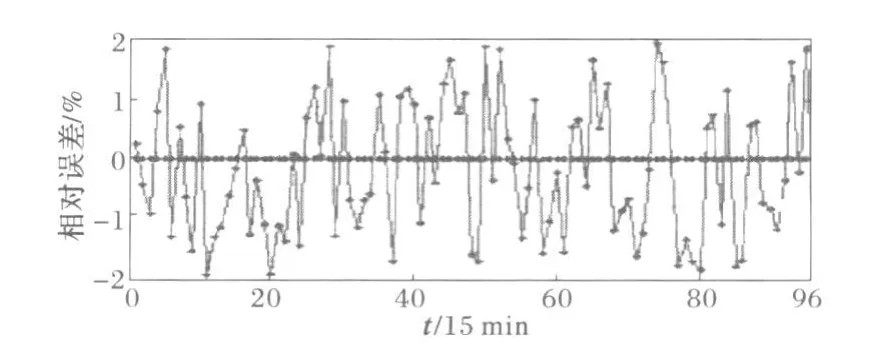
图8 相对误差分布Fig.8 Distribution of relative errors

表2 误差统计情况Tab.2 Statistics of errors

5 结语

本文充分利用小波分析、神经网络二者的优势结合起来给短期负荷预测(日预测)建模，并在小波函数及其变换尺度选择，特别是神经网络选择和建模方面进行了较为详细的探讨，并给出自己的见解和择优方案。在仅考虑历史负荷的情况下，实例分析结果表明该方法能获得较为理想的预测精度，并具有较强的应用可行性。

短期电力负荷预测是一个非常复杂的时间序列，经受各种复杂因素的影响，本文提出的预测模型尽管具有相当理想的精度，但为了更加具有实践作用，还可以从以下几方面来完善和展望。

(1)尽量将影响负荷的干扰因素量化进预测输入序列，比如说气象预报数据、节假日负荷影响等等，当然这其中存在一个非常关键的问题是这些一般来说都是定性的干扰因素如何去合适地定量化，定量不当的话反而会影响预测效果，这在考虑多因素输入时必须重点考虑。

(2)在小波分析环节，由于小波变换只对信号的低频部分进行分解，高频部分虽然是信号的细节部分，但同样隐藏着信号的一些特征和规律，如果能够对高低频同时进行分解，无疑可以一定程度上提取原信号的更多特征和规律。基于这一考虑，采用能对高频进行分解的小波包变换不失为一个值得尝试的选择[12]。

(3)应用小波分解不可避免地会产生子序列误差累加，对最终预测精度产生影响。为了有效地减少累加误差，首先须按照4.1节确定合适的小波分解水平;其次，若不考虑模型结构复杂程度的话，可以尝试对低频也就是周期性相对较强的序列用传统的自回归等方法进行预测，可以更好地控制子序列误差，从而减少累计误差。

(4)在LMBP网络预测环节，本文提出的小波子序列分时段预测模型兼备了精度要求和性能要求，即在较高精度要求前提下尽量缩短预测时间和设备开销，理论和实例测算表明这是一个小波-ANN预测中比较合适的方案。

[1] Boggess A.小波与傅里叶分析基础[M].芮国胜译.北京:电子工业出版社，2004.

[2] Simon H.神经网络原理[M].叶世伟译.北京:机械工业出版社，2004.

[3] 杨福生.小波变换的工程分析与应用[M].北京:科学出版社，2000.

[4] 张德丰.Matlab小波分析与工程应用[M].北京:国防工业出版社，2007.

[5] 飞思科技编著.小波分析理论与MAT LAB7实现[M].北京:电子工业出版社，2005.

[6] 飞思科技编著.神经网络理论与MAT LAB7实现[M].北京:电子工业出版社，2005.

[7] 宋超，黄民翔，叶剑斌(Song Chao，Huang Minxiang，Ye Jianbin).小波分析方法在电力系统短期负荷预测中的应用(The application and problems of wavelets used in short-term power load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2002，14(3):8-12.

[8] 邰能灵，侯志俭，李涛，等(Tai Nengling，Hou Zhijian，Li Tao，et al).基于小波分析的电力系统短期负荷预测方法(New principle based on wavelet transform for power system short-term load forecasting)[J].中国电机工程学报(Proceedings of the CSEE)，2003，23(1):45-50.

[9] 向峥嵘，王学平(Xiang Zhengrong，Wang Xueping).基于小波-神经网络的电力系统短期负荷预测(Forecasting approach to short-time load using wavelet decomposition and artificial neural network)[J].系统仿真学报(Journal of System Simulation)，2008，20(18):5018-5020.

[10] 顾洁(Gu Jie).应用小波分析进行短期负荷预测(Application of wavelet analysis to short-term load forecasting of power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2003，15(2):40-44，65.

[11] 徐军华，刘天琪(Xu Junhua，Liu Tianqi).基于小波分解和人工神经网络的短期负荷预测(An approach to short-term load forecasting based on wavelet transform and artificial neural network)[J].电网技术(Power System Technology)，2004 ，28(8):30-33.

[12] 熊媛(Xiong Yuan).基于小波包变换的短期电力负荷预测(Short-term Load ForecastingBased on Wavelet-Package Transforming)[D].贵阳:贵州大学电气工程学院(Guiyang:Electrical Engineering College，Guizhou University)，2002.

[13] 王黎明(Wang Liming).电力系统中短期负荷预测的研究(Research on Middle-term and Short-term Load Forecasting of Electric Power System)[D].东营:中国石油大学信息与控制工程学院(Dongying:College of Information and Control Engineering，China University of Petroleum)，2008.

[14] Drezga I，Rahman S.Input variable selection for ANN-based short-term load forecasting[J].IEEE T rans on Power Systems，1998 ，13(4):1238-1244.

[15] Kim Chang-Il，Yu In-Keun，Song Y H.Kohonen neural network and wavelet transform based approach to short-term load forecasting[J].Electric Power Systems Research ，2002，63(3):169-176.

[16] Charyloniuk W，Chen Mo-Shing.Very short-term load forecasting using artificial neural networks[J].IEEE T rans on Power Systems，2000，15(1):263-268.

[17] Hippert H S，Pedreira C E，Souza R C.Neural networks for short-term load forcasting:A review and evaluation[J].IEEE Trans on Power Systems，2001 ，16(1):44-55.