流化床提升管内气固两相流动压降的预测及试验验证

陈鸿伟, 史 洋, 李德育, 刘焕志, 危日光, 尹 萍

(1.华北电力大学电站设备状态监测与控制教育部重点实验室,保定 071003；2.天津陈塘热电有限公司,天津 300223)

循环流化床具有高效、低污染的优点,因而在煤燃烧和气化、生物质资源化利用以及固体废弃物处理等方面得到了广泛应用[1-2].气固提升管是循环流化床的关键部件,提升管内颗粒浓度的分布直接关系到气固两相的停留时间、气固两相之间的反应和传递速率以及气固两相与提升管壁和内构件表面之间的传热速率和磨损行为[3-4].因此,掌握提升管内颗粒浓度的轴向分布特性对于循环流化床的应用与设计极为重要.提升管截面的平均颗粒浓度通常可以采用压差法测试,该方法通过直接在提升管上测量压差换算得到浓度,由于应用方便、不干涉流场且适用于设备的在线监测,因而得到广泛应用.但是,在由压差换算为颗粒浓度的过程中,因难以估计颗粒加速效应及颗粒与管壁摩擦效应的影响,通常将其忽略,所以得到的颗粒浓度并非真实颗粒浓度,称为表观浓度.Van Swaaij等采用γ射线测试提升管内的真实颗粒浓度,并将其与表观浓度进行了比较,结果发现:在提升管上部稀相段,摩擦产生的压降占总压降的20%～40%,但在颗粒浓度较高时,其所占的比例下降为25%[5]；Arena采用快关阀门的研究表明:在提升管下部加速段,表观浓度与真实浓度差异很大[6].尽管表观浓度与真实浓度的差异是客观存在的,但由于压差法的方便性,不少研究者仍直接采用压差法测试结果(表观浓度)来描述提升管内的气固两相流动力学行为.

笔者设计并搭建了双循环流化床冷态试验台,利用差压变送器对上行气固提升管内轴向压降进行了系统测试,研究了颗粒循环流率对压降的影响.同时,还提出了预测提升管内压降的计算式,式中考虑了气固两相加速效应及其与管壁摩擦效应的影响,并通过冷态试验验证了该式的正确性,从而提高了利用压差法测试提升管截面颗粒平均浓度的准确性.这不仅对气固提升管内相关过程的模拟和装置的设计具有重要的实用价值,同时也为建立完善的提升管气固两相流动压降预测模型提供了参考.

1 提升管压降预测模型的建立

对于气固两相在提升管内产生的压降Δppt,应考虑与其相关的6个因素[7]:颗粒相重位压差、气体相重位压差、颗粒相加速效应、气体相加速效应、气体相与提升管壁的摩擦效应以及颗粒相与提升管壁的摩擦效应.

利用式(1)进行提升管压降计算:

式中:Lpt为提升管的长度；ε为提升管内颗粒相的空隙率；ρs为颗粒相的真实密度；ρf为空气密度；Up为提升管内颗粒相的速度；Uf为提升管内风速；Ffw为单位体积气体与提升管壁面之间的摩擦力；Fpw为单位体积颗粒与提升管壁面之间的摩擦力.

由于提升管壁面光滑,气体相与提升管壁摩擦产生的压降占总压降比例较少,Ffw可忽略不计.Fpw可由下式计算得出[7]:

式中:Gpt为颗粒通过提升管的循环流率；Dpt为提升管内径.

提升管内颗粒相的空隙率可由下式计算:

将式(2)和式(3)代入式(1)可得:

对于提升管中颗粒相的速度Up,本文考虑两个计算模型.

(1)提升管中颗粒相速度Up可根据滑移因子ψ计算[8]:

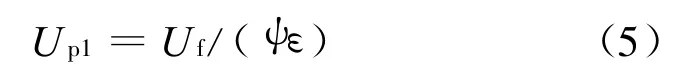
对式(3)和式(5)进行整理得:

滑移因子ψ可由下式计算[8]:

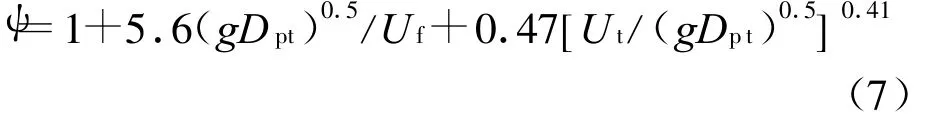
式中:Ut为颗粒相的终端速度.

(2)假定提升管中气固两相的滑移速度Uslip等于颗粒相的终端速度Ut,则颗粒相的速度Up可由下式计算:

对式(8)进行求解可得:

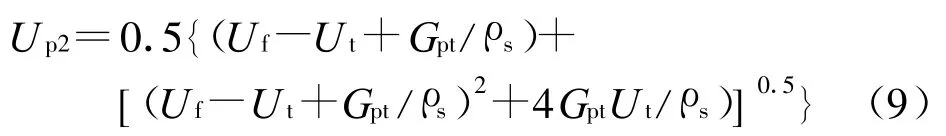
颗粒相终端速度Ut可由下式计算[9]:

式中:dp为颗粒相的平均直径；φs为颗粒的球形度.

2 试验部分

2.1 试验设备

图1为双循环流化床冷态试验装置示意图.试验装置包括提升管、鼓泡床、旋风分离器和下料管等.提升管内径为75 mm,高度为6 m,鼓泡床高度为2 m,截面为370 mm×80 mm,返料管和两级旋风分离器将提升管和鼓泡床连接成一个完整的循环系统.试验台主体部分由有机玻璃制成,便于观察物料的运动情况和测量颗粒的循环量.提升管和鼓泡床的流化气体为常温空气,由鼓风机提供,风量由蝶阀控制并由空气转子流量计测量.

在提升管不同高度处设置5个内径为5 mm的压差测试孔,测试孔距提升管布风板的高度分别为1.4 m 、2.58 m 、2.98 m、4.56 m 和 4.96 m,利用压差变送器测量不同测点之间的压差值,记为Δpij(i和j为测试孔序号).试验用压差变送器型号为JYB-G.

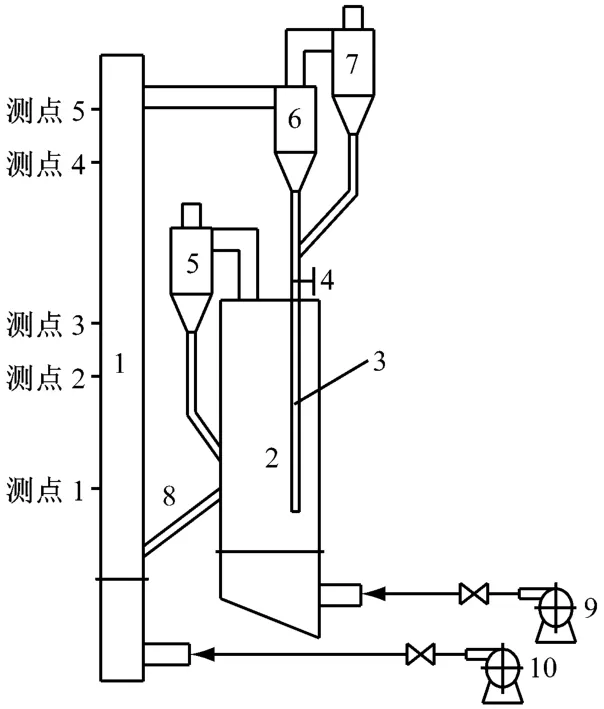
图1 双循环流化床试验装置示意图Fig.1 Schematic of the double circulating fluidized bed test rig

2.2 试验方法与内容

试验主要研究颗粒循环流率对提升管内气固两相压降的影响.颗粒循环流率的测量方法为:瞬时关闭蝶阀4,同时开始计时,观察一定时间内物料积累的高度,根据物料的堆积密度计算出物料的颗粒循环流率.

采用的床料为普通河沙,其粒径范围为0.18～0.39 mm,球形度为0.58,采用的颗粒平均粒径dp分别为0.196 mm和0.256 mm；鼓泡床静止料层高度H为0.2 m.

2.3 试验结果与分析

2.3.1 提升管底部加速段的压降

根据提升管内颗粒的运动速度分布,可将提升管分为底部的颗粒加速段和上部的充分发展段.在提升管底部加速段,颗粒垂直方向的平均速度由接近零加速到某一较稳定的速度,因此不仅要考虑气固两相与提升管壁摩擦效应产生的压降,还必须考虑颗粒相和气体相加速效应产生的压降.在提升管内风速Uf=5.66 m/s时,利用压差变送器测量测试孔1、2和测试孔1、3之间的压差.图2给出了颗粒循环流率对提升管底部加速段压降的影响.

从图2可以看出,在提升管底部加速段,假定提升管气固两相的滑移速度Uslip等于颗粒相的终端速度Ut,计算得到颗粒相速度Up,将Up代入式(4),最终得到的提升管压降预测值与试验值比较吻合.由此可见,本文提出的气固两相摩擦效应产生压降和气固两相加速效应产生压降的假设是合理的,从而证明式(1)对于预测提升管底部加速段的压降具有现实意义.

图2 颗粒循环流率Gpt对压降Δp12和Δp13的影响Fig.2 Particle circulation rate Gptvs.pressure drop Δp12and Δp13

2.3.2 提升管充分发展段的压降

当颗粒进入提升管底部时,其所受到的气体曳力大于重力,因而向上作加速流动.随着颗粒的加速,气固两相间的滑移速度减小,气体曳力也随之减小,当气体曳力减小到等于颗粒重力时,颗粒加速过程结束,进入等速流动阶段.考虑到本试验中颗粒循环流率不大,颗粒向上运动到距提升管布风板3.84 m时,就已过渡到提升管的充分发展段.在计算提升管充分发展段的压降时,气固两相的加速效应已经不存在,仅需考虑颗粒相与管壁的摩擦效应,因此式(4)可以简化为:

将各操作条件下的颗粒循环流率值代入式(11),计算得到相应的压降,并与试验测得的压降进行对比,结果示于图3.

图3 颗粒循环流率Gpt对压降Δp45的影响Fig.3 Particle circulation rate Gptvs.pressure drop Δp45

由图3可以看出,在提升管充分发展段,利用滑移因子ψ计算颗粒相速度Up的值,代入式(11)中得到的压降与试验值比较吻合,可见在提升管充分发展段仅需考虑颗粒相与管壁的摩擦效应,式(11)对于预测提升管充分发展段的压降具有实际意义.

3 结 论

(1)在计算提升管底部加速段的压降时,必须考虑气固两相的加速效应以及颗粒相与提升管壁的摩擦效应.通过比较预测值和试验值发现,假定提升管气固两相的滑移速度Uslip等于颗粒相的终端速度Ut,计算得到颗粒相速度Up,代入式(4)中得到的提升管压降预测值与试验值比较吻合.

(2)在提升管充分发展段,颗粒相加速过程已经结束并进入等速流动阶段,计算压降时,不再考虑气固两相的加速效应,仅考虑颗粒相与提升管壁的摩擦效应.通过比较预测值和试验值发现,利用滑移因子ψ计算得到颗粒相速度Up,将Up代入式(11)中得到的提升管压降预测值与试验值比较吻合.

[1] M URAKAMI Takahiro,XU Guangwen,SUDA Toshiyuki,etal.Some process fundamentals of biomass gasification in dual fluidized bed[J].Fuel,2007,86(1):244-255.

[2] 方梦祥,施正伦,王勤辉,等.内循环流化床煤气化炉的试验研究和设计[J].动力工程,2003,23(4):2525-2529.FANG Mengxiang,SHI Zhenglun,WANG Qinhui,et al.Experimental research and design of coal gasifier based on inter-circulating fluidized bed[J].Journal of Power Engineering,2003,23(4):2525-2529.

[3] 胡国新,李艳红,程惠尔.循环流化床中的气固两相传热模型[J].动力工程,2006,21(3):1219-1223.HU Guoxin,LI Yanhong,CHENG Huier.Influence of particle cluster on gas-solid heat transfer in a circulating fluidized bed[J].Journal of Power Engineering,2006,21(3):1219-1223.

[4] BAI D R,JIN Y,YU Z Q,et al.The axial distribution of the cross-sectionally averaged voidage in fast fluidized beds[J].Powder Technology,1992,71(1):51-58.

[5] VAN SWAAIJ W P M,BUU RM AN C,VAN BREUGEL J W.Shear stresses on the wall of a dense-solids riser[J].ChemEng Sci,1970,25(1):1818-1820.

[6] ARENA U,CAMM AROTA A,PISTONE L.High velocity fluidization behavior of solids in a laboratory scale circulating fluidized bed[M].Toronto:Pergamon Press,1986:119-125.

[7] HENTHORN K H,PARK K,CURTIS J S.Measurement and prediction of pressure drop in pneumatic conveying:effect of particle characteristics,mass loading,and Reynolds number[J].Ind Eng Chem Res,2005,44(14):5090-5098.

[8] GUPTA S K,BERRUTI F.Evaluation of the gas-solid suspension density in CFB risers with exit effects[J].Powder Technology,2000,108(1):21-31.

[9] 吕俊复,张建胜,岳光溪.循环流化床锅炉运行与检修[M].北京:中国水利水电出版社,2003:17-19.