传输线分布参数模型与物理模型

2010-08-16唐正明

电气电子教学学报 2010年6期

关键词：高等教育出版社传输线端口

朱峰,唐正明,2

(1.西南交通大学电气工程学院电工电子系,四川成都 610031;2.西华师范大学物理与电子信息学院,四川南充 637002)

1 问题的提出

关于传输线的二端口模型,我国教科书、专著[1-4]及一些学术论文[5-6]的分析都是这样表述的:当传输线物理线路尺度与载波波长能够满足L≥λ/100时,电路分析中的集中参数模型便不再适用。

此时分析线路中的电压、电流须用分布参数模型,如图1所示。

此时的电路微分关系为

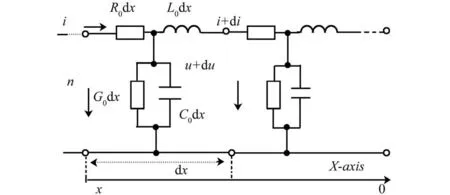
图1 分布参数的端口模型

式(1)便是大家熟悉的传输线动力学方程。通过求解该微分方程,就能得出电压和电流的位置和时间关系。文献[1]给出了由空间电场、磁场与电压、电流的过渡程式,是目前国内教材的典型代表。

对此,特别是在频域情形下,可以给出电压、电流复向量形式的齐次微分方程为

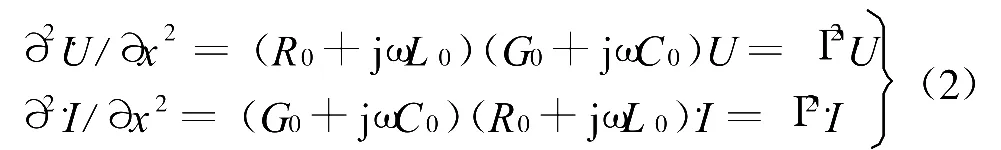
可以得到的通解形式为

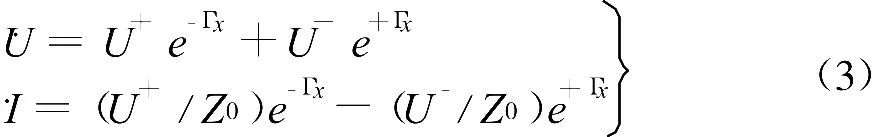
由此表明线中电压、电流具有波动特性。通过给出初始位置的电压、电流的条件便能够得到电压、电流的分布。笔者在研究生“电磁兼容”课程教学中,遇到学生提出这样的问题:图1中的端口模型中上下两根线,上面那根线存在电位分布,而下面那根地线作为参考是处处等电位。而从真实的物理模型来看,下边那根线也应该存在电位分布。这一点,对“电磁兼容”课程的教学而言非常重要。因为就电磁干扰来说,在考虑数据线的干扰传播及耦合特性分析时,这种单纯的端口模型显然就不合适了,进行过程分析时,必须考虑真实的物理模型;也只有理解真实的物理模型,才能从真正意义上理解分布参数的端口模型。

2 分布参数的物理模型

如图2所示,上下两根传输线都通有电流,均存在分布电阻。为便于与图1相对应,分布电阻R0在对称位置各取1/2,分布电感L0也是如此。文献[7-8]虽也有这种假设,但未能给出时域微分过程,只是考虑了无耗的频域近似模型。

图2 分布参数的物理模型

现在,设某位置x处的上下线点的电位分别为u1和u′1。通过dx距离后,在x+dx处所对应的电位为u2和u′2。分别考虑每根线上的电压和对称电流对应的微分过程,则有

令端口 x处电压u1-u′1以及 x+dx处电压为u2-u′2,并设两点端口所对应的电位差为du,则由上式得

由此可见

至此,我们完成了从物理模型到端口模型的过渡。由上式可以看出,正确理解端口模型,要注意以下几个关键问题。

(1)本质上而言,端口概念只是一种数学抽象,真实的物理过程被隐藏了起来,因这种抽象能够体现出电压和电流的波动特性而被广为采用。由本推导可以看出,分布参数模型,规定下面那根线均为零参考电位,并无本质上的物理意义;

(2)现存的教科书均以L≥λ/100作为分布参数模型的判据。但我们认为,还应该注意两传输线的线间距离d。由于线间距离通常非常小,大多数教材均未提。只有文献[2]提及线间距离d远小于波长方可适用。从物理本意来看,线间距离d要小到集中参数模型的定义范畴。由此可以推断,分布参数模型实质上是一种近似模型,存在的纵向条件为线间距离至少要满足d<λ/100,才能保证模型的准确性。我们认为,这一点具有重要的应用价值。例如,考虑电气化列车的电磁干扰,若干扰频率为300MHz,对应的波长为1米,但接触线只是一根线,是靠大地作为回流对列车进行驱动的。此时,由于供电线和地之间距离有6.5米,远大于1米,此时电容的概念已经不存在,故利用传输线模型分析电磁干扰没有意义,只能利用场方程的方法进行求解。