布尔函数相关免疫性与平衡性关系的研究
2010-08-14李卫卫
李卫卫
(上海政法学院 现代教育技术中心,上海 201701)
1 引言
布尔函数的相关免疫性是保证密码系统具有良好安全性的重要性质。布尔函数的导数(偏导数)的概念和性质是人们早已熟知的,但导数(偏导数)只能反映布尔函数内部一个方面值的结构特点。因而在讨论布尔函数的相关免疫性时,没有什么用途。在文献[1,2]中引入布尔函数的e导数能刻画布尔函数内部值的另一种特点的结构,将其和导数一起深入到布尔函数的内部结构中,从布尔函数内部不同特点的结构对相关免疫性的影响来分析布尔函数的平衡性与相关免疫性的关系,可得出有关布尔函数相关免疫性有意义的新结果,同时,也为更好地研究布尔函数的密码学性质保证密码系统的安全性指引了一个新的研究方向。
2 预备知识
首先,对e导数的概念和与本文有关的性质做简要叙述。
定义1[1]布尔函数 f( x)的多元e导数为
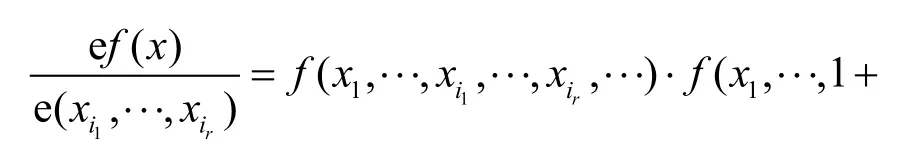

若r=1,则布尔函数f( x)对单个变元xi的e导数记为ef( x)/exi,即

定义2[2]布尔函数f( x)对单个变元xi的导数记为df( x)/dxi,定义为

定义3[2]布尔函数f( x)对多个变元xi的导数记为df( x)/d(xi1,···xir),即

下面不加证明地给出2个有关导数和e导数的性质引理。
引理1[3]布尔函数f( x)是平衡H布尔函数,当且仅当w(df( x)/dxi)=2n-1,且w(e f( x)/exi)=2n-2,i=1,2,···,n
引理2[3]对布尔函数f( x),
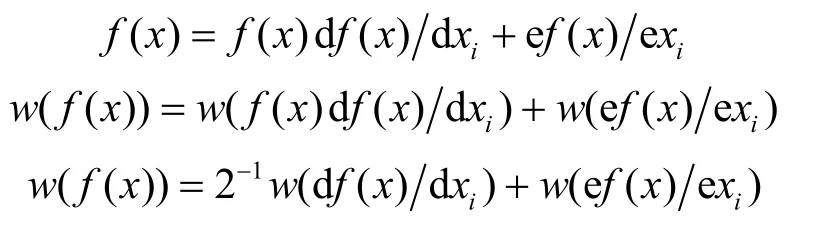
其取值范围i=1,2,···,n。
3 平衡布尔函数的一阶相关免疫性的判定
通过对平衡布尔函数一阶相关免疫性的研究,可以简化检测平衡布尔函数是否一阶相关免疫的计算,能很容易地构造高维一阶相关免疫的平衡布尔函数,从而得出许多重要的密码学性质定理。
定理1 n维平衡布尔函数f( x), x=(x1,x2,···,xn)由2个n-1维布尔函数fp(x)和fq(x),其中x=(x1,x2,···,xn)级联构成:f( x)=(1+x1)fp(x)+x1fq(x)。
1) 平衡布尔函数f( x)若有

则f( x)是一阶相关免疫函数。
2) 若平衡布尔函数f( x)是一阶相关免疫函数,则w( fp( x))n-1=w( fq( x))n-1=2n-2,且w(e fp(x)exn)=w(e fq(x)exn)。
证明 ① 当式(1)成立,且f( x)是平衡布尔函数,则由偏导数的定义便知,对an∈GF(2)[3](GF(2)表示伽罗华域),有w( f( x)|xn=an)=2-1w( f( x))=2n-2。取a∈GF(2)n,且w( a)=n,则式(1)等价于w( f( x+a)+f( x ))=0,f( x+a)=f( x)。故对任意xi, i=1,2,···,n ,有

由于w( f( x))=w( xif( x))+w((1+xi) f( x))=2n-1,再由式(2)及f( x+a)的意义便知
故对任意xi, i=1,2,···,n ,有

故知f( x)是一阶相关免疫函数。
② 若f( x)是一阶相关免疫的平衡布尔函数,则必有式(4)成立,于是在式(4)中,取xi为x1,便知
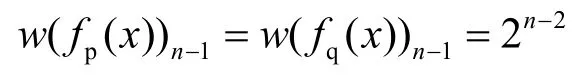
而在式(4)中,取xi为xn-1和1+xn-1,便知:w(e fp(x)exn)=w(e fq(x)exn)。
4 平衡布尔函数二阶相关免疫性的判定及其构造
定理1说明一阶相关免疫的平衡布尔函数(且非线性函数[4])是易于构造的,那么是否存在并同样易于构造出二阶相关免疫的平衡布尔函数?下面来讨论这一问题。给出一个平衡布尔函数一阶相关免疫的充分性定理。
定理2 f( x)为平衡布尔函数,
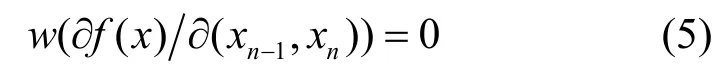
且w( ef( x)exn)=0,则f( x)是一阶相关免疫函数。
证明 若式(5)成立,则f( x)在xx···x00~xx···x11取值范围内对f( x)均有xn=0和xn=1处的值相等。又由于f( x)为平衡布尔函数,故对an∈GF(2),有
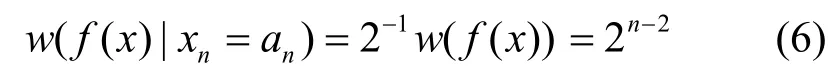
由于w(e f( x)/exn)=0,故f( x)在上述各取值范围内的值均相等,均为

故知

由各取值范围内的值均相等及式(6)和式(7)可知,对xi( i≠n-1,n)也有

故由式(6)、式(8)和式(9)可知,对ai∈GF(2)n[5],有w( f( x)|xi=ai)=2n-2,即f( x)是一阶相关免疫的平衡布尔函数。
现在来讨论平衡布尔函数二阶相关免疫的判定问题。该问题也是在密码学领域中一直没有得到很好解决的难点问题之一,而下面的定理3、定理4给出了一个较之简单的解决方法。同时,也给出了一个构造三阶相关免疫[6]的平衡布尔函数的方法。
定理3 设g( x), x=(x1, x2,···,xn-2)是n-2元的一阶相关免疫的平衡布尔函数,则n元布尔函数f( x)=g( x)+xn-1+xn是三阶相关免疫的平衡布尔函数。
证明 先证明对任意n-2元布尔函数g( x),n元布尔函数f( x)=g( x)+xn-1+xn都是一阶相关免疫的平衡布尔函数。

故w( f( x))=2-1w(df( x)dxn)+w(e f( x)exn)=2n-1,可知f( x)是平衡布尔函数。
由于

由f( x)是平衡布尔函数,式(10)和式(11)及定理2可知,f( x)是一阶相关免疫的平衡布尔函数。于是有
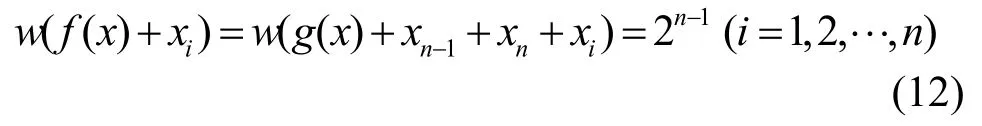
由开始处证明的结论便知,对i≠j(i, j=1,2,···,n -2)时,
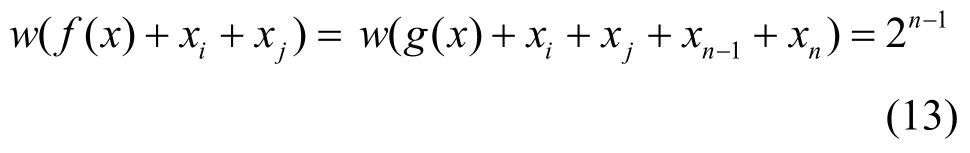
由式(12)知,对i≠j,当i=n-1,j≠n或i=n, j≠n -1时,由g( x)的任意性有
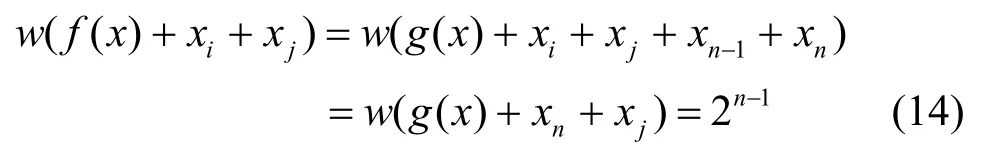
或
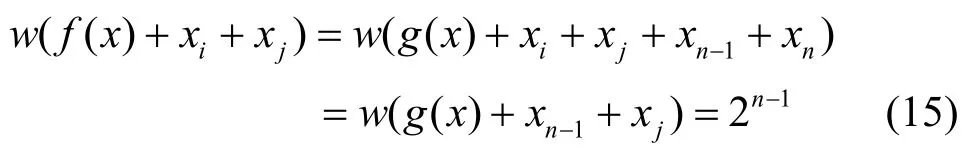
而当i=n-1,j=n时,由于g( x)是任意n-2元平衡布尔函数,故
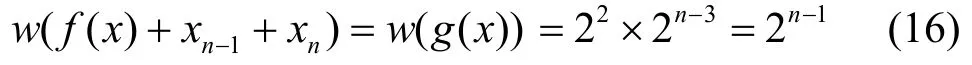
由式(13)~式(16)可知f( x)是二阶相关免疫平衡布尔函数。
同样,对i≠j≠k(i, j, k=1,2,···,n-2),由开始的证明可知,g( x)+xi+xj+xk是与xn-1,xn无关的n-2元布尔函数。及
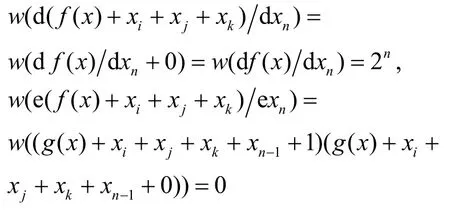
故

同样由式(12)及式(12)中g( x)是任意n-2元布尔函数,故对i≠j≠k,i, j, k中有1个而且只有1个变元是xn-1或xn,而其余2个变元均不为xn-1或xn。不妨设xi=xn-1或xn,则有

或
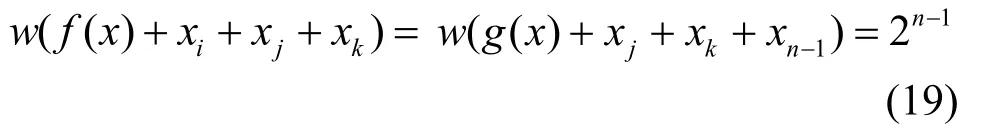
当i≠j≠k(i, j, k=1,2,···,n-2),且i, j, k中有1个为xn-1,1个为xn时,不妨设xi=xn-1,xj=xn,由于g( x)是一阶相关免疫函数,故有
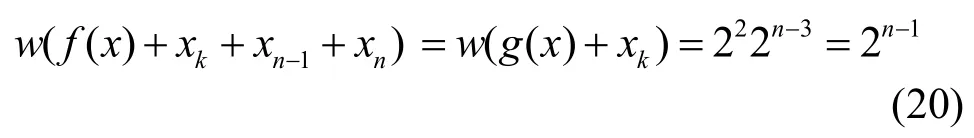
由式(17)~式(20)可知,f( x)是三阶相关免疫的平衡布尔函数。
从定理3的证明,显然可得到如下推论。
推论1 设g( x), x=(x1, x2,···,xn-2)是n-2元的平衡布尔函数,则n元布尔函数f( x)=g( x)+xn-1+xn是二阶相关免疫的平衡布尔函数。
推论2 设g( x), x=(x1, x2,···,xn-2)是n-2元布尔函数,则n元布尔函数f( x)=g( x)+xn-1+xn是相关免疫的平衡布尔函数。
定理3实际上给出了一个构造三阶相关免疫的平衡布尔函数的方法[7]。判断一个平衡布尔函数是二阶相关免疫函数,判断工作量是很大的,但定义了e导数以后,可以得到一个判断平衡布尔函数二阶相关免疫的较简单方便的方法。因此有下面的定理。
定理4 设f( x)为非线性布尔函数,若
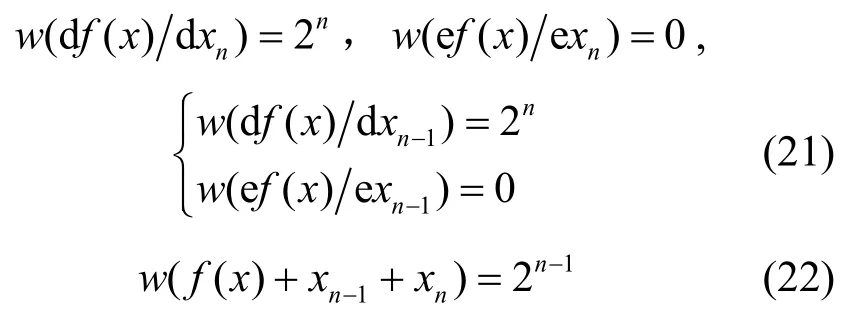
则f( x)是二阶相关免疫的平衡布尔函数。
证明 由式(21)便知,f( x)是平衡布尔函数。

故f( x)+xi+xn一定与xn无关,所以f( x)一定为如下函数f( x)=g( x)+xn(其中g( x)与xn无关)。
同样由于w(df( x)dxn-1)=2n,故对i=1,2,···,n-1,n,有

因此,f( x)+xi+xn-1一定与xn-1无关,故f( x)一定是如下函数。

其中,g1( x)+xn-1=g( x),且g1( x)是与xn-1及xn无关的非线性函数。
由式(23)及推论2,便知f( x)是一阶相关免疫的平衡布尔函数。当i, j=1,2,···,n-2,且i≠j(其中r=n-1或r=n)。有
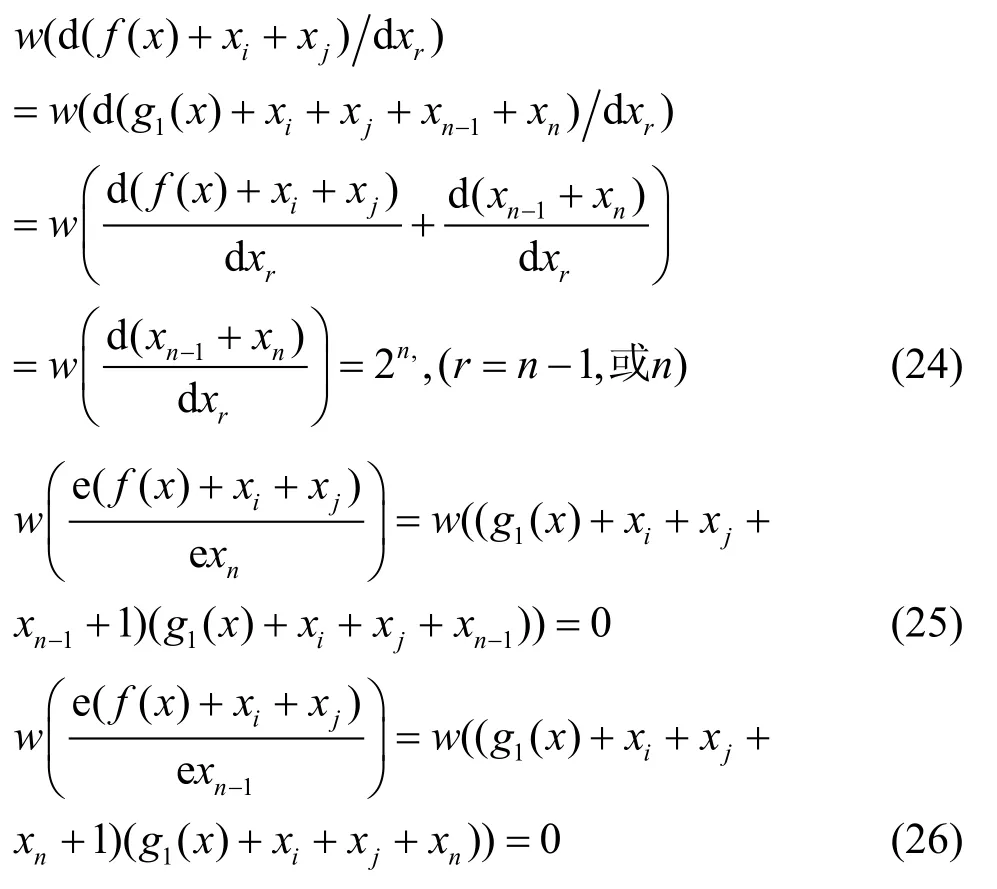
故知

取xj=xn-1,i=1,2,···n-1,n,有

故
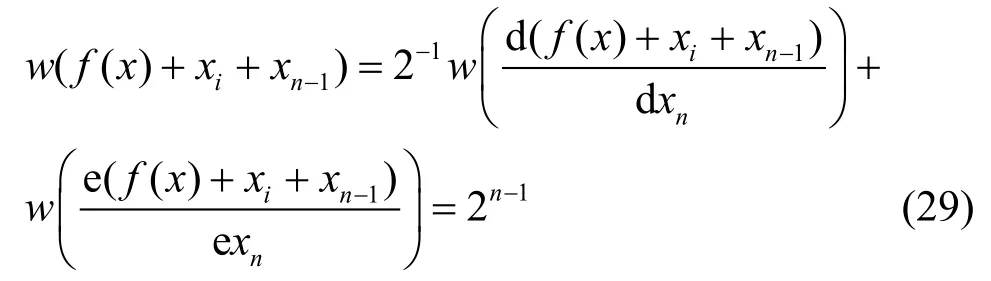
同理,取xj=xn,i=1,2,···,n -1,也有

于是由式(27)、式(29)、式(30),便知对一切i=1,2,···,n-1,n,且i≠j,均有式(22),即w( f( x)+xi+xj)=2n-1,故知f( x)是二阶相关免疫的平衡布尔函数。证毕。
由定理4的证明,还可得到如下推论。
推论3 设f( x)为非线性平衡布尔函数,若式(21)成立,则:
1) f( x)是一阶相关免疫的平衡布尔函数;
2) f( x)一定为式(23),即f( x)=g1( x)+xn-1+xn(其中g1( x)是与xn-1、xn无关的n-2元布尔函数);
3) 式若(27)成立,则g1( x)是n-2元平衡布尔函数。
推论3的第1个和第2个结论在定理4中已给出了详细的证明,而第3个结论只需要由w( f( x)+xn-1+xn)=w( g1( x))n=2n-1,即知w( g1( x))n-2=2(n-2)-1,故结论成立。
由定理3和定理4显然还可得到如下推论4。
推论4 若f( x)是三阶相关免疫的平衡布尔函数,且满足定理4的式(21)和式(22),则:f( x)=g1( x)+xn-1+xn,其中g1( x)是与xn-1、xn无关的n-2元一阶相关免疫的平衡布尔函数。
从定理3和定理4的证明中可看出,在定理的这种构造相关免疫函数的方法中,扩散性[8]对免疫性没有影响。
5 结束语
从文中的讨论及结论可知,用e导数(e偏导数)和导数(偏导数)深入到布尔函数的内部结构中,可以较容易地得到相关免疫性的有意义的结论,得出一些有用的且能揭示满足相关免疫性的平衡布尔函数结构特点的性质,如判断相关免疫性、构造相关免疫函数等密码系统所需的内容[9~11]。进一步揭示了布尔函数优良的密码学性质,为更好地研究布尔函数的密码学性质保证密码系统的安全性和抗攻击性打下了基础。
[1] LI W W, WANG Z. The E-derivative of Boolean functions and its application in the fault detection and cryptographic system[A]. The 5th IIGSS Workshop, Kybetrnetes[C]. 2007.245-249.
[2] 温巧燕, 钮心忻, 杨义先. 现代密码学中的布尔函数[M]. 北京: 科学出版社, 2000. 31-33.WEN Q Y, NIU X X, YANG Y X. Boolean Function in Modern Cryptoloy[M]. Beijing: Science Publishing House, 2000. 31-33.
[3] 李卫卫, 王卓. E-导数和导数在布尔函数中的应用[A]. 中国通信学会第五届学术年会论文集[C]. 2008.267-270.LI W W, WANG Z. The application of derivative and E-derivative on H-Boolean functions[A]. The 5th China Institute of Communications Collected Papers[C]. 2008. 267-270.
[4] GUO Y F, LAN L Y. Balanced correlation-immune functions[J]. China Science and Technology Information, 2006, 20(8): 22-25.
[5] XIAO G Z, MASSEY J L. A spectral characterization of correlation-immune combining functions[J]. IEEE Trans on Inform Theory,1988, 34(3): 725-728.
[6] MO J. The construction and enumeration of symmetric balanced Boolean functions[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(5): 5-8.
[7] 张串绒, 肖国镇. 一类布尔函数的性质和应用[J]. 通信技术,2001,16(2):11-14.ZHANG C R, XIAO G Z. Properties and applications of a class of Boolean functions[J]. Communications Technology, 2001, 16 (2):11-14.
[8] HE L S. On Boolean functions with highest algebraic immune degree[J]. Chinese Journal of Computers, 2006, 29(9): 1579-1583.
[9] ZHANG W G, XIAO G Z. A characterization of algebraic immune Boolean functions[J]. Journal of Beijing University of Posts and Telecommunications, 2007, 30(5): 56-57.
[10] LUO W H, LI C. Algebraic immunity study of Boolean functions[J].Computer Engineering and Applications, 2007, 43(8): 59-60.
[11] SIEGENTHALER T. Correlation-immunity of nonlinear combining functions for cryptographic applications[J]. IEEE Trans, 1984, 30(5):776-778.
