GPS-RTK用于海上高程放样

2010-08-13夏显文

中国港湾建设 2010年6期

夏显文

（中交第三航务工程局有限公司，上海 200032）

0 引言

海上项目的施工由于其地理位置的特殊性，无法用常规水准方法进行高程放样，GPS-RTK以其快速、高效、远距离和不受通视影响等特点成为海上施工测量的首选方法。根据以往的经验，RTK的平面精度已经能够达到相应的等级要求，但由于存在高程异常的问题，使得RTK直接测得的GPS大地高不能简单地转换到正常高。

应用GPS-RTK方法进行施工放样必须进行WGS84坐标与工程坐标的转换，由此涉及到转换精度的问题，通常采用点校正的方法检测坐标转换的精度，点校正的精度高低直接影响流动站测量的结果，一般来说，参加点校正的控制点应该包围整个测区[1]，但是由于海上工程的特殊性很难达到这个要求，因此，在这样的条件下，采用RTK放样能否达到设计精度要求值得探讨。

本文以某海上测风塔施工项目的实例数据分析，讨论了基于七参数坐标转换的GPS-RTK高程测量方法，并与高程拟合方法进行比较，通过采用国家测绘部门提供的高程异常数据对两种方法得到的高程精度进行检核。结果表明该工程在已知GPS水准点较少的情况下，坐标转换方法的精度要优于常规的高程拟合法，并且能够满足施工精度要求。

1 原理方法

目前，GPS-RTK高程测量的主要方法是坐标转换和高程拟合[2]。坐标转换以七参数转换法为主；高程拟合的方法很多，常用的有：多项式拟合法、多面函数法、加权平均法以及神经网络法等。

1.1 七参数坐标转换

Bursa-Wolf模型是空间七参数坐标转换常用的数学模型[3]，其表示如下：

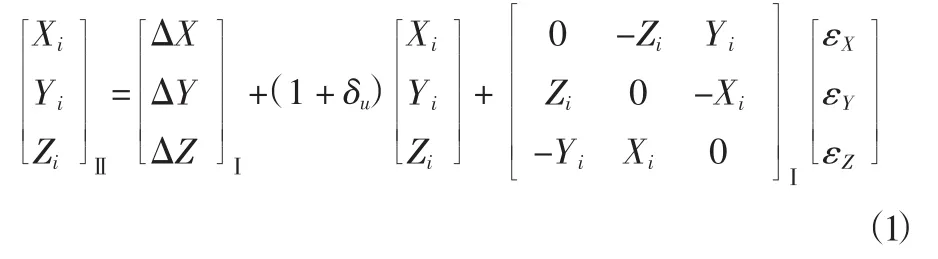
式中：下标Ⅰ、Ⅱ分别表示两个不同坐标基准下的空间直角坐标。式中7个待求参数被称为七参数：ΔX、ΔY、ΔZ为3个平移参数，δu为尺度参数，εX、εY、εZ为3个旋转欧拉角。

由式（1）可知，未知参数为7个，则至少需要3个已知公共点才可求得。在实际运用中，通常取n（n≥3）个已知公共点，构成3n个误差方程，根据最小二乘法求出七参数。

1.2 高程拟合方法

高程拟合法的基本思想是：在范围不大的区域，高程异常具有一定的几何相关性，根据这一特点，对于GPS与几何水准重合点的高程异常值及点的坐标，建立测区高程异常分布的数值模型，解算出拟合模型的参数，再通过该模型求该测区其他点的高程异常值。较常用的有以下方法：

1.2.1 曲面拟合

当GPS网布设成网状时，一般采用曲面拟合法，设测站点的高程异常值ζi与坐标（xi，yi）之间存在以下函数关系：

式中：f（xi，yi）为拟合模型即高程异常的近似值；εi为拟合误差。

曲面拟合高程异常的数学模型为：

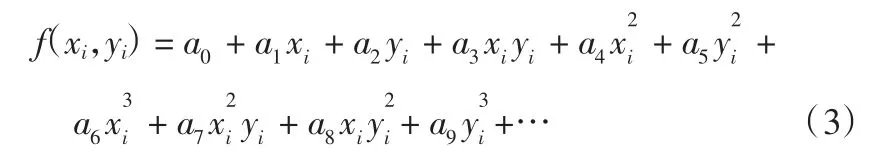
式中：a为拟合系数；i=1，2，…，m，m为水准重合点数，当m大于系数a的个数时，根据ε2=min求其最小二乘解，进而求出测区范围内任意插值点的高程异常值。

根据所选参数项不同可分为：平面拟合、相关平面拟合、六参数拟合等，其参数项分别对应式（3）中的前三项、前四项、前六项。

1.2.2 加权平均法

设在内插点周围有n个已知点，高程异常为ζi（i=1，2，…，n），对应的权为Pi，则内插点j的高程异常为：

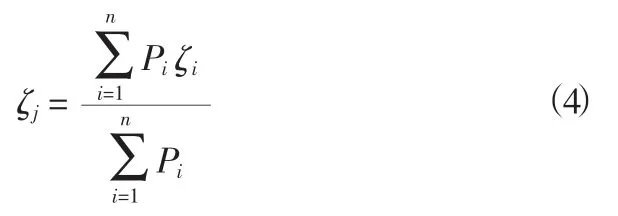
Pi可根据已知点到内插点的水平距离Dij来计算[4]：

2 工程实例

2.1 工程概况

本单位承接了某海测风塔基础工程，该工程位于霞浦县三沙镇近海侧离岸约9.5 km。由于大规模建造风力发电场还没有确定，工程的大型首级控制网没有布设。业主只提供一个测风塔的中心位置坐标、设计高程和结构图及设计要求。

测风塔基础由3根钢桩组成，桩顶高程＋9.850 m（国家85高程基准），基础顶面高程＋10.00 m。测风塔用于测量该海域不同海拔高度的风力资源，以确定将来在此大规模建造风力发电场的风力发电机叶片的高度，所以对高程的要求较高，其误差不大于10 cm。平面位置要求测风塔中心位置在50 cm以内，组成测风塔基础的桩基相对位置误差不大于15 cm。另外，因工程需要，已获得霞浦县三沙镇附近的4个城建C级控制点（54北京坐标+85高程基准）的坐标。

2.2 工程应用

为提高坐标转换参数的精度，对已有的4个控制点及用作参考站的CKZ1点布网（图1）采用静态模式进行测量，目的是这样解算出来的七参数与实地的椭球系统会更加接近[5]。

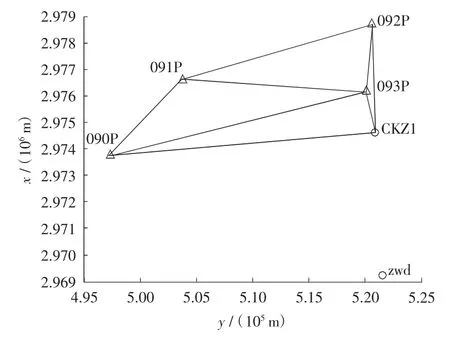
图1 施工控制网图

由于提供的4个控制点与测风塔zwd点不在同一投影带中，因此，需要首先将已知坐标换算到施工坐标系中，结果如表1所示。分别投入天宝R8 GNSS双频接收机5台，仪器标称精度为±（5 mm+0.5×10-6D），D为测段的距离，按城建三等GPS控制网规范要求进行观测。基线向量解算采用广播星历和商用软件，统一应用Leica公司的LGO软件将原始观测文件转换为RINEX文件后进行基线解算，以保证其数据的一致性，采用随机商用软件解算静态基线。其闭合差满足城建三等GPS控制网规范要求，然后在WGS84系统下进行无约束平差，得到结果如表2所示。

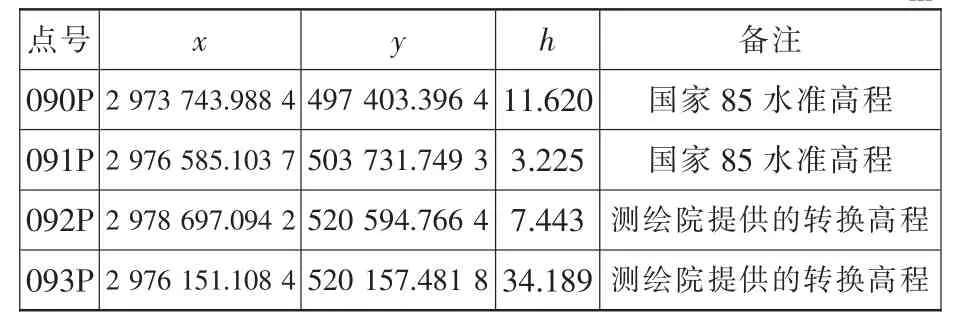
表1 转换到施工坐标系的控制点坐标表m

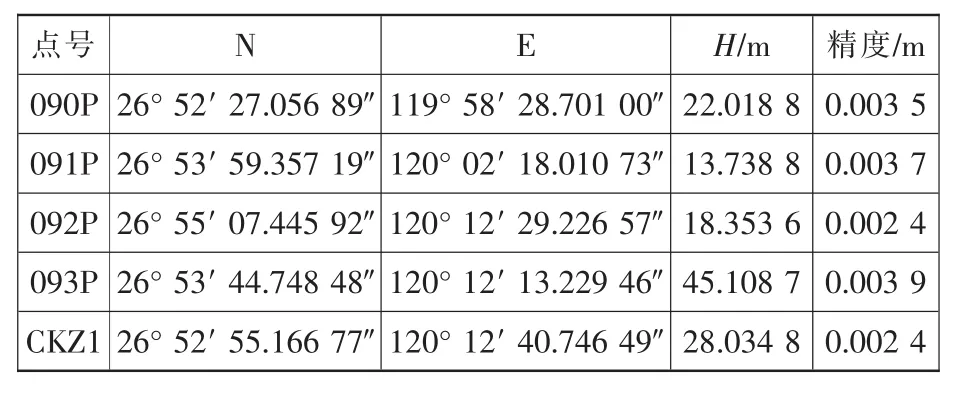
表2 WGS84平差成果表

选择了七参数作为基准转换方法，首先利用控制点的WGS84坐标、平面坐标和正常高以及相应的投影变换参数来计算七参数。关于RTK作业精度，国家及行业规范目前还没有相应的规定，在测量应用中，通常是通过检核已知控制点坐标作为检核条件来鉴定作业精度的可靠性[6]。图2为控制点坐标转换残差图。

由图2的结果表明：用于计算基准转换的控制点坐标都符合较好，平面和高程的转换残差均小于5 mm，内符合精度分别为：X坐标1.8 mm，Y坐标1.9 mm，高程4.6 mm。

由于布设GPS首级控制网时未与国家GPS控制点联测，所以平差所得的GWS84坐标与国家测绘第一大队所提供的高程异常有一个常数差值C，我们取4个控制点高程与国家提供的高程异常的差值的均值来反映这个常数差值C，计算得C=1.889 m。

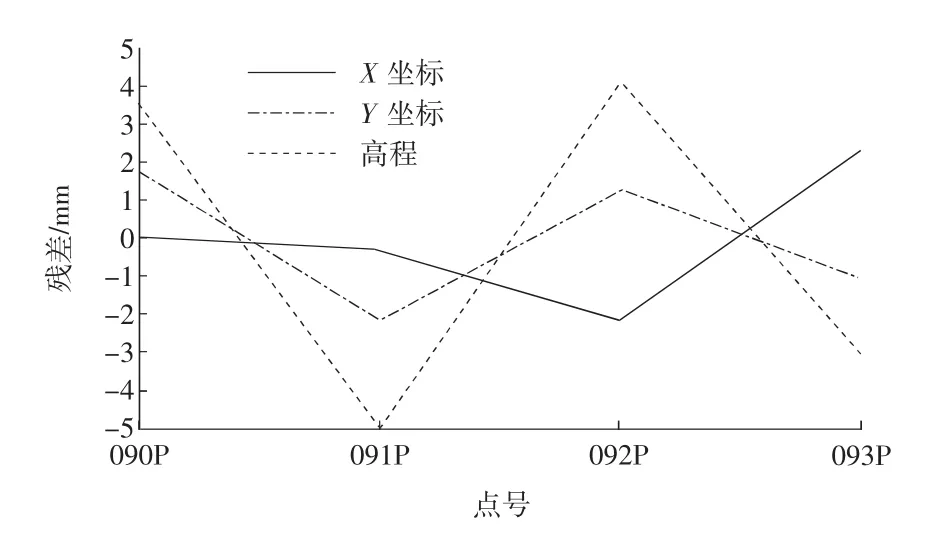
图2 控制点七参数坐标转换残差图

再根据各点GWS84的大地高、高程异常及所求的常数值求得各点的高程与设计提供的国家85高程进行对比，以判断转化七参数的准确性，并与高程拟合的平面拟合法，相关平面拟合和加权平均法进行比较，结果见表3。

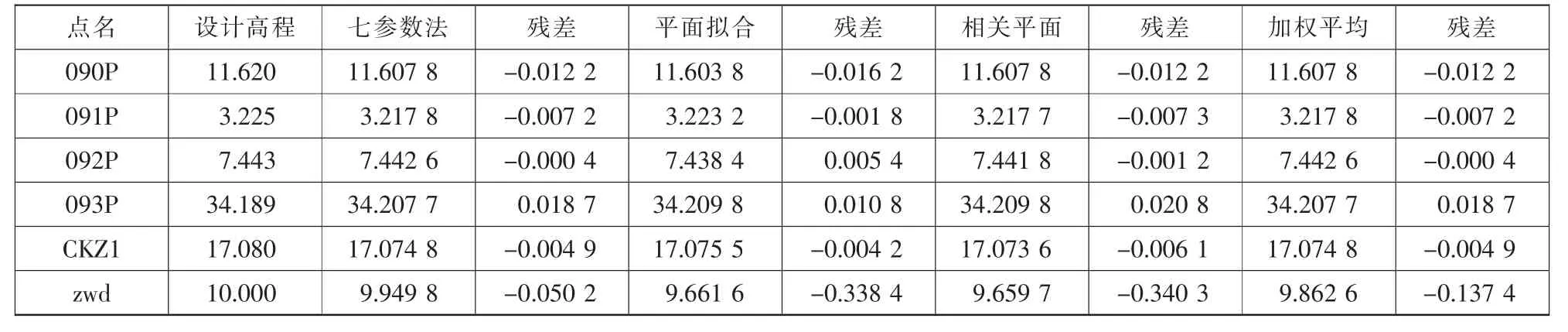
表3 坐标转换与高程拟合比较表m

2.3 结果分析

由表3的结果可以看出，在该海上工程中，通过坐标转换方法得到的放样点zwd的误差大约为5 cm，满足设计限差10 cm的要求，表明通过公共点得到的坐标转换参数是准确的，同时也验证了七参数坐标转换的高程用于此类海上工程测量是可行的。另外，由于RTK默认流动站的高程异常和基准站是相同的[7]，也证明了在离海岸小范围海域的高程异常与海岸高程异常相差很小，在海岸点设置基准站，其高程测量精度能够满足施工精度要求。

而运用高程拟合法得到的结果超出了设计要求的10 cm限差，分析其原因主要为：1）已知点数目过少（只有5个点），曲面拟合在曲面类型的选取和最小二乘计算方面受到制约，使模型不能很好地与实际地形吻合，导致放样点精度不高；2）根据以往经验，已知点的位置对水准拟合的精度影响很大，拟合点外推的精度不可靠[8]，而本文实际工程受地理环境限制，拟合点位于测区的边缘外侧，采用外推的方式导致拟合高程精度偏低。