大空间柱壳结构爆炸动力响应的Ritz-POD数值模拟

高轩能,王书鹏

(华侨大学土木工程学院,福建 泉州362021)

大空间柱壳结构具有造型美观、受力合理、杆件种类单一、制作安装方便和空间视觉好等特点,在大跨度、大柱网的公共建筑中得到广泛应用。由于人群活动密集,这类大空间公共建筑也易于成为恐怖爆炸袭击的目标,一旦发生,常造成重大人员和财产损失。对于大空间公共建筑的室内恐怖爆炸,防备更难,损失更大。因此,迫切需要对大空间建筑进行内爆炸下的动力响应及抗爆防护措施进行研究[1-2]。

大空间柱壳结构为空间受力结构体系,杆件多、自振频率分布密集、结构的动力响应需要考虑多阶模态的影响及不同模态间的耦合效应,使大空间柱壳结构在爆炸作用下的结构响应分析非常复杂[3-4]。此外,在内爆炸作用下,大空间结构除承受冲击波荷载外,还要承受高温、高压对结构形成的准静态气体压力[5-6]。为此,各国学者做了大量研究工作,并形成了结构抗爆设计的技术标准,但相关研究多数仅涉及军事工程领域,对于民用建筑结构研究不多[1-2,7-11],难以直接用于民用建筑的抗爆和防爆设计。迄今为止,大空间柱面网壳结构在内爆炸下的压力场分布规律及其动力响应等问题仍未得到有效解决[12-13]。文章对大空间柱壳结构的动力特性进行分析,应用LS-DYNA有限元程序建立大空间钢柱壳结构在内爆炸作用下的实验模型[14],并对模型及参数选取的正确性及可靠性进行比较验证。在此基础上,采用Ritz-POD法对大空间柱壳结构在内爆炸荷载下的动力响应进行数值模拟计算,并研究结构不同变化因素对结构动力响应特性的影响。

1 大空间柱面网壳结构的自振特性

大空间结构模型采用 3向网格单层柱面钢网壳,横向跨度B=20m,纵向长度 L=40m,矢跨比F/B=1/5(或1/4、1/2),周边固支支承,支座下围护墙体高 H=10m(或 6m、8m、12m),杆件钢材Q235,无缝钢管,焊接球节点,其中纵轴向杆件为φ89×4mm,斜向杆件为 φ140×6mm。结构模型及网格划分如图1所示。

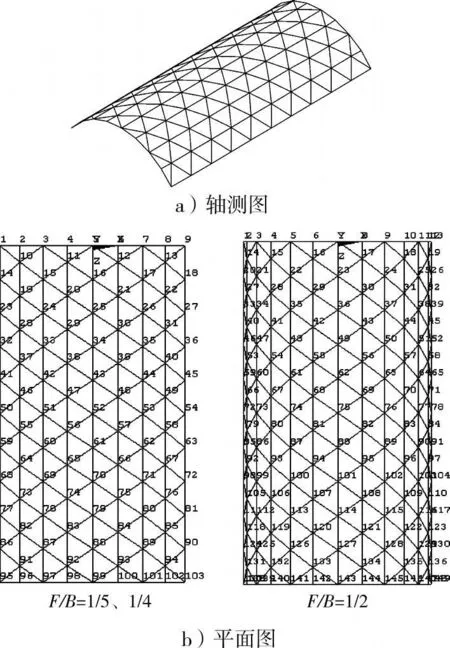
图1 大空间柱面网壳模型

对上述结构模型进行动力特性分析,3种不同矢跨比下的前50阶自振频率的分布如图2所示。

图2 大空间柱面网壳结构自振频率

为了更直观地了解大空间柱面网壳结构的振动特性,图3给出了矢跨比F/B=1/5时的前10阶振型。从图中可以看出,1阶振型呈现半波状,以中线x=10m为对称轴正对称振动,结构中心振幅最大,为竖向振动;2阶振型在x向为一个波,y向为半波,以中线x=10m为对称轴呈反对称、中线y=20m为对称轴呈正对称振动,为水平振动;之后各阶振型呈现的半波数随自振频率的增加而增加,或为水平振动,或为竖向振动,依其自振频率特性出现。

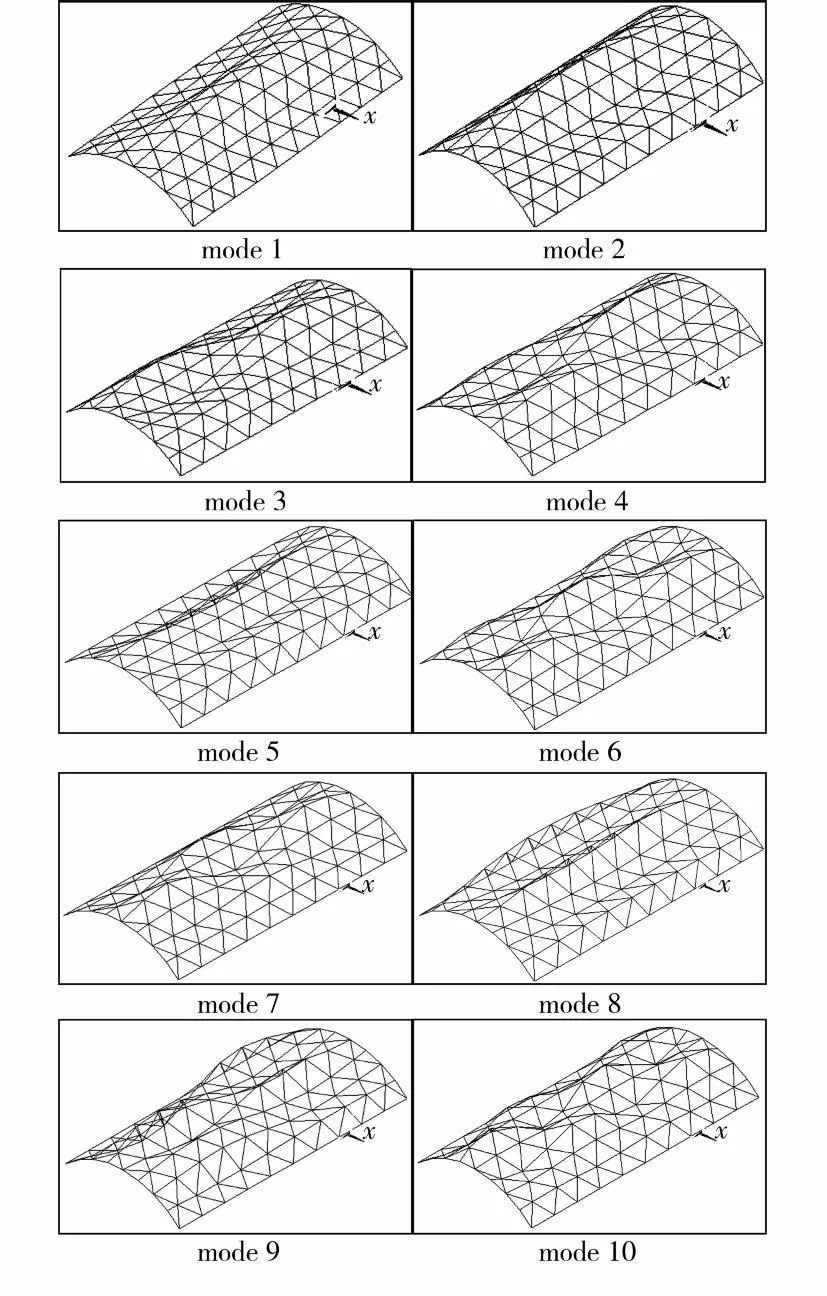
图3 柱面网壳结构的前10阶振型图(F/B=1/5)

由此可见,3种不同矢跨比下大空间柱面网壳结构的固有频率分布非常密集,频谱相近,振型复杂,对于爆炸冲击荷载作用下的压力分布及动力响应分析,采用一般的振型向量叠加法求解常常需要考虑几十甚至上百个振型,计算量巨大。同样,爆炸冲击荷载作用时间极短,结构在爆炸冲击荷载下的最大响应多发生在冲击后,采用直接积分法求解其在爆炸荷载下的响应常常需要考虑足够大的时间步才可能获得稳定可靠的数值解,计算量也惊人,在现有微机条件下将很难实现。为此,将Ritz向量叠加法与POD法结合,利用有限测点的表征数据将存在时空差异的冲击波转换为在同一时间坐标下来表示,就解决了动力响应计算量大和困难的问题。

2 内爆炸数值实验模型及其验证

2.1 结构与材料参数取值

大空间结构模型如前所述,应用LS-DYNA有限元程序建立大空间柱壳结构室内爆炸数值实验模型。计算模型考虑5种物质的相互作用,选用3种单元。网壳结构、地面和墙体均假设为刚体,以便考虑空气冲击波压力场分布。空气和炸药采用Solid164单元,地面和围护墙体采用Shell163单元,结构杆件采用Link160单元。

炸药采用MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程,空气采用MAT_NULL材料模型和线性多项式状态方程EOS_LINEAR_PLLYNOMIAL。炸药的材料参数取值如下:密度ρ=1 630 kg/m3,初始体积v0=1.0,初始内能 E0=8×109J/m3,爆速 D=6 713m/s3,爆压 PCJ=18.5 GPa,输入参数 A=540.9 GPa,B=9.4 GPa,R1=4.5,R2=1.1,Ω=0.35。空气的材料参数为:密度ρ=1.290 kg/m3,初始体积V0=1.0,初始内能E0=2.5×10-5J/m3,输入参数c0=c1=c2=c3=c6=0,c4=c5=0.4。

为简化计算,利用对称性取1/2模型分析。除对称面外,边界面为透射边界以模拟在无限区域的爆炸。文章重点考虑人体炸弹等恐怖因素对大空间结构的爆炸效应,取爆炸点高度离地面1.2m计算。

2.2 数值实验模型的验证

材料参数取值的合适与否,直接影响到数值模拟计算结果的准确性。采用LS-DYNA程序对炸药在无限空中爆炸进行了数值模拟计算,以验证材料参数取值的正确性和可靠性。取炸药尺寸0.2m×0.2m×0.2m,空气尺寸12m×12m×12m,边界面设为透射边界。数值模拟计算的冲击波超压与3个经验公式[15-16]的计算结果都很接近,而与Henrych公式计算结果最为吻合。超压持续时间则与Henrych经验公式结果几乎一致,表明结构模型和材料参数的取值是正确而适用的,具体过程与结果可参见文献[17]。

3 Ritz-POD法在结构内爆炸动力响应中的应用

3.1 Ritz向量叠加法

Ritz向量叠加法的本质就是设法产生一组与动荷载空间分布有关而正交的Ritz向量,然后利用它们来求解结构的受迫振动。本征正交分解(POD)法的本质则是寻找一个空间函数 φ(x,y,z),用于描述由时间和空间位置2类参数确定的爆炸冲击波压力场。Ritz向量叠加法的第1组基向量是以{φ}k为荷载的静力反应,且相互正交。其他Ritz向量用以反映动力惯性力的影响。爆炸冲击荷载经过POD分解后,荷载向量可表示为:

式中,{φ}k表示第k阶本征模态,ak(t)表示第k阶本征模态的时间坐标。

Ritz向量叠加法的主要计算步骤如下[18]:

1)产生第1组基向量{U}1,k(每个基向量对应相应的荷载空间分布{φ}k,k=1,2,…,m)

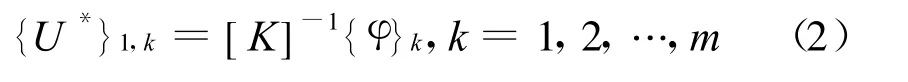
正则化,

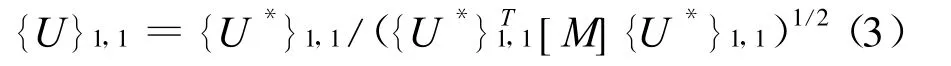
正交化,

正则化,

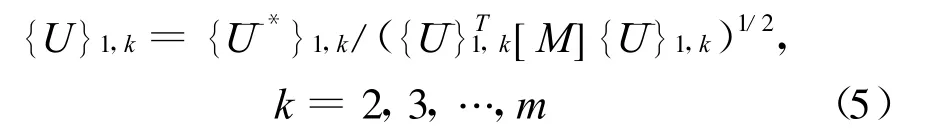
2)产生其他初始向量{U}j,k(j=2,3,…,p,p≪n,n为结构自由度)

正交化,

正则化,

至此,可得:

3)产生对[K]正交的向量,令:

则由

可以得到 λi和{a}i,i=1,2,…,m◦p。则结构的m◦p阶Ritz向量即可表示为:

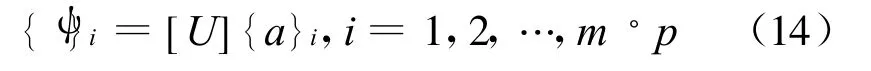
与传统的振型叠加法相比,Ritz-POD法在计算结构爆炸动力响应方面有其独特优点[19-20]。设2个向量X={x1,x2,…,xn}和Y={y 1,y2,…,yn}的夹角的余弦为:

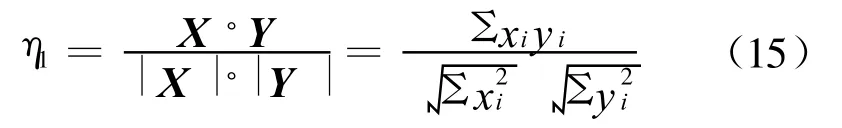
此2向量的模的比值为:

此2向量非常相近的必要条件为η1和η2都要接近于1。只要2个指标的其中之一与1相差较大,则表明2个向量有较大差别。

表1为根据式(15)和式(16)准则,分别采用以上2种方法求得的柱壳结构上跨中节点52和任选节点38(如图1(b)所示)达到最大位移时的全部节点位移分布的计算精度。其中,向量X表示根据传统振型叠加法或Ritz-POD法计算所列节点位移达到最大值时结构各节点的位移向量,向量Y表示节点位移准确值构成的向量。

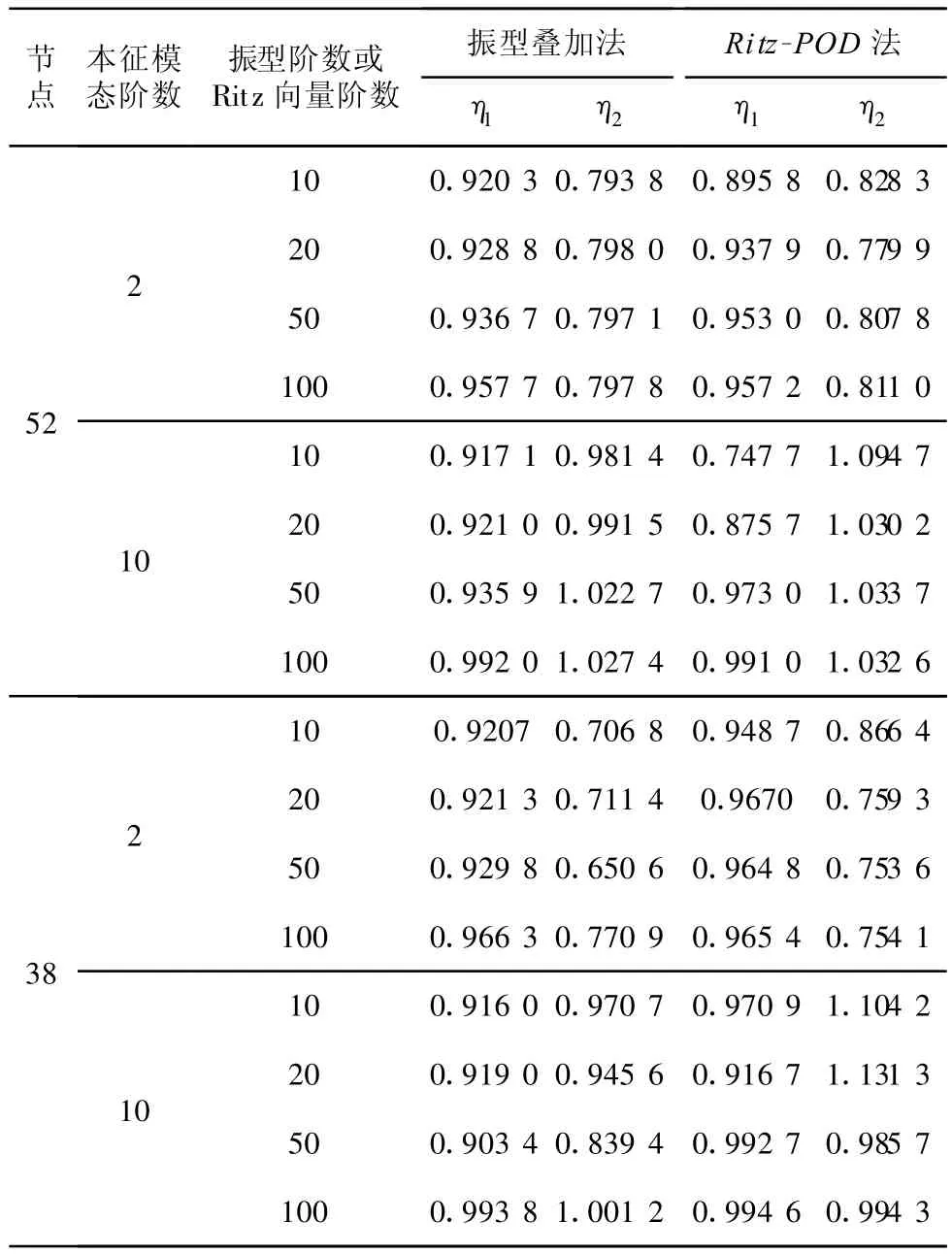
表1 位移响应振型叠加法与Ritz-POD法的计算结果

从表中可以看出,本征模态阶数取2时,2种方法求得的节点位移分布精度均较好,说明前2阶本征模态已经能够很好的描述整个冲击波压力场的分布,在振型阶数相同的情况下,Ritz-POD法计算各节点位移分布呈现出较好的计算效率和计算精度。本征模态阶数取10时,Ritz向量阶数较小情况下,Ritz-POD法计算各节点位移分布反而不如采用传统振型分解法计算各节点位移分布的精度,Ritz向量阶数较大时,Ritz-POD法计算各节点位移分布的精度才较好,说明要取得较好的计算效率和精度,必须控制Ritz向量阶数与本征模态阶数的比值,该比值越大,采用Ritz-POD法计算的效率和精度会越好。由此可知,Ritz-POD法特别适合自振频率分布密集的柱壳结构的动力响应计算。

3.2 Ritz-POD数值模拟结果及分析

爆炸冲击波压力场的确定是大空间结构爆炸动力研究的前提,对大空间结构进行爆炸模拟计算后,提取结构表面n个点处的冲击波超压数值并将其进行POD分解,即可得到结构的第k阶模态相应的冲击波压力场分布,详可参见文献[12]。对于前文所述结构模型,应用Ritz-POD法,即可得到结构在爆炸冲击荷载作用下的动力响应。为简化计算,做以下假设[18]:1)结构可有效卸爆,即围护结构物在爆炸瞬间破坏,不会对结构形成准静态气体压力;2)结构构件上的爆炸冲击波荷载按线性分布考虑,以构件两端节点处的模态值表示。

1)矢跨比对结构动力响应的影响。计算模型为柱面网壳结构B×L×H=20m×40m×10m,矢跨比F/B分别取为 1/5、1/4、1/2,炸药 TNT当量体积为0.5m×0.5m×0.5m,炸药高度1.2m,爆炸点在结构中心,其他参数如前所述。结构的最大位移响应及响应时间如图4所示,杆件最大应力响应及响应时间如图5所示。

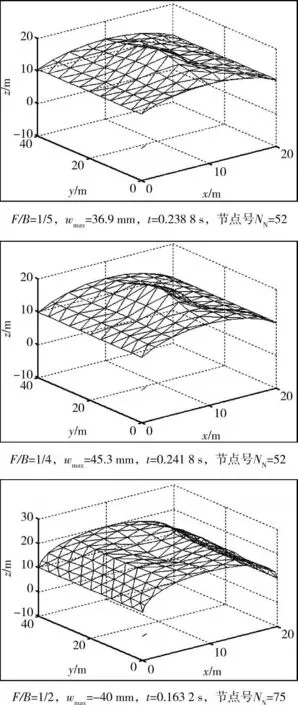
图4 柱壳结构的最大位移响应图

图5 柱壳结构的最大应力响应图

从图4和图5可以看出,在爆炸冲击荷载作用下,矢跨比对结构的位移响应影响较显著。结构最大位移均在中心节点处,但达到最大位移响应的时间、大小和方向有所不同。随着矢跨比的增大,结构的最大位移响应由正向增加反转为负值,出现变号现象并始终在跨中,对应的响应时间也是略微变长后变为较短。与位移响应不同,随着矢跨比的增大,结构的最大应力响应逐渐减小,但对应的响应时间和位置规律性不强。F/B=1/5和1/2的结构最大应力响应均在靠近支座处的杆件上,而 F/B=1/4的结构最大应力响应则在靠近跨中的杆件上,且对应的响应时间也无规律可言。总体而言,当大空间柱壳结构的抗爆设计以位移为控制条件时,矢跨比较小的结构较好。当以应力为控制条件时,矢跨比为1/2的圆柱壳结构抗爆性能最好。

2)爆炸点对结构动力响应的影响。计算模型为柱面网壳结构B×L×H=20m×40m×10m,矢跨比F/B=1/4,炸药TNT当量体积为0.5m×0.5m。×0.5m,炸药高度1.2m,爆炸点沿横向对称轴距结构纵向中线(坐标值x=10m)的坐标分别为0m、2.5m、5.0m和7.5m,其他参数如前所述。结构的最大位移响应及响应时间如图6所示,杆件最大应力响应及响应时间如图7所示。

图6 不同爆炸点下柱壳结构的最大位移响应图

从图6和图7可以看出,在不同爆炸点情况下,大跨度柱壳结构在爆炸冲击荷载作用下的最大位移响应和最大应力响应呈现出了较明显的规律性。1)结构最大位移响应均出现在跨中节点处(节点号=52)。2)如图6所示,最大位移响应随爆炸点偏心距的增加起伏不定,但总体呈减小的趋势。爆炸点位于结构中心时,位移响应最大。3)如图7所示,不论爆炸点在何处,结构的最大应力响应时间接近且与最大位移响应不同步,均小于最大位移响应时间。4)除爆炸点在跨中外,最大应力杆件均出现在靠近支座的杆件中。爆炸点距结构中心愈大,结构的最大应力响应位置愈靠近支座,杆件的最大应力值也随偏心距的增大而增加。表明对于大空间结构,偏心爆炸比中心爆炸冲击波对结构构件的损害大,特别是对于应力控制设计的结构,应更注重支座附近结构的防护。

4 结语

应用ANSYS/LS-DYNA程序,通过对大空间柱壳结构在内爆炸荷载作用下的数值模拟实验,建立了进行动力响应计算的合适模型。将Ritz振型叠加法与POD法结合,解决了冲击波荷载的时空差异性和结构表面压力场分布问题以及结构爆炸动力响应计算量大的难题。对大空间柱面网壳结构在内爆炸冲击荷载作用下的动力响应进行了数值模拟计算与分析,可得到如下结论:

1)矢跨比和爆炸点位置对结构的位移和应力响应均有较大影响。总体来说,矢跨比大的结构防(抗)爆炸冲击波的能力较强。但以位移为控制条件时,矢跨比较小的结构抗爆性能较好;以应力为控制条件时,矢跨比为1/2的圆柱壳结构抗爆性能最好。

2)偏心爆炸比中心爆炸对大空间结构构件的损害大,偏心爆炸对结构的边跨构件最为不利。偏心愈大,结构的最大应力响应位置愈靠近支座,杆件中的最大应力值也愈大。因此,设计中应更注重加强支座和边跨结构的防(抗)爆能力。

鉴于问题的复杂性,研究忽略了结构几何非线性和材料非线性的影响。对于大空间结构在爆炸荷载作用下应力响应和位移响应的精确分析,尚需考虑结构几何和材料双非线性的影响,这有待更深入的研究。

[1]杜修力,廖维张,田志敏,等.爆炸作用下建(构)筑物动力响应与防护措施研究进展[J].北京工业大学学报,2008,34(3):277-287.DU XIU-LI,LIAO WEI-ZHANG,TIAN ZHI-MIN,et al.State-of-the-art in thEdynamic responses and blast resistantmeasures of thEbuildings under explosiveloads[J].Journal of Beijing University of Technology,2008,34(3):277-287.

[2]孙建运,李国强.建筑结构抗爆设计研究发展概述[J].四川建筑科学研究.2007,33(2):4-10.SUN JIAN-YUN,LI GUO-QIANG.Summarization on thEdesign of architecturEand structurEengineering to resist blast load[J].Sichuan Building Science,2007,33(2):4-10.

[3]李国豪.工程结构抗爆动力学[M].上海:上海科学技术出版社,1989.

[4]周岱,刘红玉,李春祥.拉索-网壳结构的动力特性和非线性动力反应[J].振动与冲击,2002,21(1):7-11.ZHOU DAI,LIU HONG-YU,LI CHUN-XIANG.Dynamic characteristics and nonlinear dynamic responses of cable-supported grid shell structures[J].Journal of Vibration and Shock,2002,21(1):7-11.

[5]DUFFEYA T A,ROMERO C.Strain growth in spherical explosivEchambers subjected to internal blast loading[J]. International Journal of Impact Engineering,2003,28:967-983.

[6]HUNG C F,LIN B J,HWANG-FUU J J,et al.Dynamic responsEof cylindrical shell structures subjected to underwater explosion[J].Ocean Engineering,2009,36:564-577.

[7]TM5-1300.Structures to resist thEeffects of accidental explosion[M].Department of thEArmy Technicalmanual,Department of thENavy Publication NAVFAC P-397,Department of thEAir Forcemanual AFM 88-22,Department of thEArmy thENavy and thEAir Force,June1969.

[8]ASCE.Design of structures to resist nuclear weapons effects[M].New York:CommitteEon Dynamic Effects of ASCE,1985.

[9]ASCE.Design of blast resistant buildings in petrochemical facilities[M].New York:TaskCommitteEon Blast Resistant Design of thEPetrochemical CommitteEof thEEnergy Division of ASCE,1997.

[10]YAO XIONG-LIANG,GUO JUN,FENG LIN-HAN,et al.Comparability research on impulsivEresponsEof doublEstiffened cylindrical shells subjected to underwater explosion[J].International Journal of Impact Engineering,2009,36:754-762.

[11]LI BING,PAN TSO-CHIEN,NAIR ANAND.A casEstudy of thEeffect of cladding panels on thEresponsEof reinforced concretEframes subjected to distant blast loadings[J].Nuclear Engineering and Design,2009,239:455-469.

[12]高轩能,王书鹏,江媛.大空间结构的爆炸冲击波压力场分布[J].北京理工大学学报,2009,29(S1):193-197.GAO XUAN-NENG,WANG SHU-PENG,JANG YUAN.ExplosivEshockwavEpressurEdistribution on largespacEstructure[J].Transactions of Beijing InstitutEof Technology,2009,29(S1):193-197.

[13]史春芳,徐赵东.工程结构抗爆技术的研究现状[J].西安建筑科技大学学报:自然科学版,2007,39(5):616-620.SHI CHUN-FANG,XU ZHAO-DONG.Anti-explosion technology in engineering structure[J].Journal of Xian University of ArchitecturE&Technology:Natural SciencEEdition,2007,39(5):616-620.

[14]LS-DYNA Keyword User'smanual[M].971st ed.LSTC,2005.

[15]李翼祺,马素贞.爆炸力学[M].北京:科学出版社,1992.

[16]J.亨利奇.爆炸动力学及其应用[M].熊建国,译.北京:科学出版社,1992.

[17]高轩能,王书鹏.大空间柱面网壳结构在爆炸荷载下的动力响应[J].振动与冲击,2009,28(10):68-73.GAO XUAN-NENG,WANG SHU-PENG.Dynamic responsEof a large-spacEcylindrical reticulated shell under blast loading[J].Journal of Vibration and Shock,2009,28(10):68-73.

[18]王书鹏.大空间钢结构的爆炸动力响应及抗爆设计方法[D].泉州:华侨大学,2008.

[19]张建胜,武岳,沈世钊.单层网壳结构风振响应的模态耦合效应分析[J].振动与冲击,2006,25(6):39-42.ZHANG JIAN-SHENG,WU YUE,SHEN SHI-ZHAO.Study onmodal coupling effect of singlElayer reticulated shell for its wind-induced vibration[J].Journal of Vibration and Shock,2006,25(6):39-42.

[20]陈波.大跨屋盖结构等效静风荷载精细化理论研究[D].哈尔滨:哈尔滨工业大学,2006.