动载作用下的大跨度双层斜拉桥组合梁桥面响应分析

杜新光,金先龙,陈向东

(上海交通大学 机械与动力工程学院,上海 20240)

移动荷载作用下的大跨度桥梁常常表现出较强的垂向、横向及扭转等耦合性,因此车辆通过时桥梁结构的桁架、板件等承受的应力与变形成为工程人员十分关心的问题。对桥梁在车辆荷载作用下动力响应问题的研究方法主要包括两大类,一些研究人员采用空间杆系或简化梁建立有限元模型,计算了移动载荷作用下桥梁的动态响应[1-5];另外一些学者通过建立桥梁的三维精细有限元模型,分别对桥梁的静力与移动载荷下的动力特性进行了分析[6-8]。可以看出,受限于计算机运算速度和容量等因素,目前的桥梁静、动力特性分析,主要采取简化模型,即使建立了三维精细有限元模型还主要集中于中短跨度的较小桥梁。

某大跨度公路-轻轨两用双层斜拉桥结构复杂,桥上行驶的轻轨车辆通行密度高、装载质量大。该文对该桥建立了精细的轨道车辆与桥梁耦合振动分析数值模型,模型的单元与节点数均超过百万。采用基于接触均衡的并行计算技术在超级计算机上进行了求解。最后比较和分析了轻轨车辆单向运行和双向汇车运行条件下,桥面关键部位桁架节点受力状态及主、边跨跨中桥面节段的动力响应特性。

1 全三维精细车桥耦合模型建立

1.1 斜拉桥模型

根据斜拉桥设计图纸建立了斜拉桥的全三维精细有限元模型,整个模型由桁架、斜拉索、主塔、墩、承台、支撑桩、土体、轨道结构组成。

斜拉桥结构的几何形状、荷载条件、边界条件、材料性质等复杂多样,对不同的桥梁结构采用不同的有限单元。土体、承台、主塔、墩、枕木、钢轨等采用实体单元建模;支撑桩采用梁单元建模;斜拉索采用只受拉不受压的索单元模拟。斜拉桥有限元模型单元和节点总数约为135万,如图1(a)所示。

图1 双层斜拉桥有限元模型

作为桥梁主要承载运输的构件,桥面采用钢板桁梁组合结构[9],主要包括图1(b)和图(c)所示的主跨和边跨2种形式,其中的直、斜腹杆和上下层桥面的弦杆均由翼板、腹板、隔板以及加劲组成。

上、下桥面为钢正交异性板和纵横梁体系,上层桥面板采用大规格U形加劲肋并设置4道小纵梁,下层设置6层小纵梁,在桁架节点处设置一道工字主横梁。

1.2 轻轨车辆模型

轻轨车辆的数值模型如图2所示,根据实际的空间位置、几何尺寸、材料特性、连接形式建立,由车体、转向架和轮对等组成多自由度的动力学系统。

图2 轻轨车辆的数值模型

轻轨车辆共有4节车厢,采用两系悬挂,一系悬挂装置和二系悬挂装置的阻尼均作为线性粘滞阻尼来处理。因此,整车车辆就具有了浮沉、横摆、摇头、点头、测滚,共有27个自由度。车辆的主要参数见表1。

表1 轻轨车辆模型的主要参数

轻轨车辆与斜拉桥之间的耦合作用通过车轮与轨道之间的滚动接触实现。将车轮上节点作为从接触点,钢轨面作为主接触面,在每一时步,搜索任一从节点最靠近的主节点,随后判断从节点是否穿透主面,无穿透则不作处理,穿透则在从节点与被穿透主表面间引入一个法向接触力[10]:

其中,ni是接触点处主单元面的外法线单位矢量,ki为主单元面的刚度因子。如果l≥0,则表示从节点没有穿透主单元面,也即两物体没有发生接触,从而实现轨道车辆的跳轨、脱轨等现象。

2 显式并行有限元分析

采用有限元法将车辆及桥梁耦合振动系统离散为一组有限个且按一定方式相互联结在一起的单元组合体。考虑个单元的总和,其平衡方程为[11]:

式中:N为插值矩阵;a为节点加速度;B为应变-位移矩阵;σ为应力向量;b为体积力载荷;F为作用牵引载荷为接触力。

经单元计算并组集后,在t时刻式(2)可写成:

对于公式(3),采用中心差分法,其关系表达式为:

根据(2)和(3),可建立时间递推公式:

在显式算法中,为了保证中心差分计算方法的稳定性,时间步长通常细分成网格中的最短自然周期。每一时刻的时步长由当前构形的稳定性条件控制,下一时步长Δtn+1取决于当前的最小值:

式中,α为比例系数,N为单元数目。而单元的极限步长Δt则由单元的特征长度和材料特性决定。

对于一般串行计算机很难完成的大规模有限模型的求解,可以采用并行计算的方法解决该问题,不同的分区策略对最终并行算法的效率好坏有着直接性和关键性的影响。目前常采用的方法是区域分割法[12-15],这些方法能够保证各个子区域单元数量相当,但对于存在大量接触的模型来说,不能保证各个节点机负载平衡。该文根据模型存在大量接触的特点,结合上海超算中心曙光4000A巨型机的体系结构,设计了基于接触均衡分区方法进行求解,该方法的并行计算原理如下:

1)根据设定的CPU个数,均分接触定义的相邻单元,划分区域边界,边界的节点被复制到对应的区域中。

2)非接触单元按照几何坐标分布到对应子区域中,直到子区域数与所用处理器的数目相等,输出分区结果。

3)节点初始化,中心差分法求解位移、速度。

4)计算单元应变力、应变率,进行分区节点通信及强迫边界条件。

5)判断计算是否终止,如果没有则返回3),如果满足终止条件,则整合各分区结果并输出。

3 结果与分析

移动轻轨车辆作用下的双层斜拉桥组合梁桥面的受力状态比较复杂,因此该文着重对桥面的边跨跨中节段和主跨跨中节段处的桁架杆件、辅助墩和过渡墩(A、B、D)以及主塔C处的杆系连接节点等关键部位的应力进行了分析,详细示意如图3所示。

图3 组合梁桥面响应分析部位示意

3.1 桥面杆系的受力状态分析

仿真计算了单向匀速行驶和双向汇车行驶2种典型的行车工况,其中单向匀速运行时,方向为从边跨向主跨;双向运行时,两车在主跨跨中位置汇车。因为轻轨车辆的车速较低,车速变化范围比较小,所以车辆都以最大运行速度80 km/h匀速过桥。

斜拉桥的桥面桁架杆系采用全焊连接的整体结构,从图4(a)中可以看出,当轻轨车辆通过桥面时,由于与支座接触和结构部件连接较多,在主塔和桥墩部位的桁架节点处出现了不同大小的应力集中现象;图4(b)中比较了轻轨车辆通过主跨时,主塔及边墩处杆系连接节点的Vonmises应力云图,从中可以看出,车辆通过主跨中段时,对主塔处节点应力的影响远大于对桥墩处。

图4 桥面关键节点处的Vonmises应力云图

图5给出了轻轨车辆通过斜拉桥时,主跨和边跨跨中节段的Vonmises应力云图分布情况。从图中可以看出,斜拉桥组合梁桥面的各构件的应力比较复杂,但斜腹杆、下横梁和上下弦杆分担了较大的载荷,并且不同构件的受力状态随着车辆的移动而发生变化。

图5 跨中节段的Vonmises应力分布云图

3.2 桥面杆系的动态响应分析

为了能更好的分析和比较桁架主跨或边跨跨中位置的斜腹杆、下弦杆、下横梁等的Vonmises应力随车辆移动的变化情况,分别提取了相应的响应时程曲线分别如图6(a)、(b)、(c)所示。

图6 主跨跨中、边跨跨中Vonmises应力变化时程曲线

从图6中的Vonmises应力变化曲线图可以看出,当车辆到达该构件位置附近时,该构件受力达到最大。

表1中列出了斜拉桥部分构件在移动载荷作用下,Vonmises应力变化的最大值计算结果。在各个构件中,下横梁所承受载荷最大,斜腹杆与下弦杆相连接的节点处为应力集中的部位,且应力变化较大。

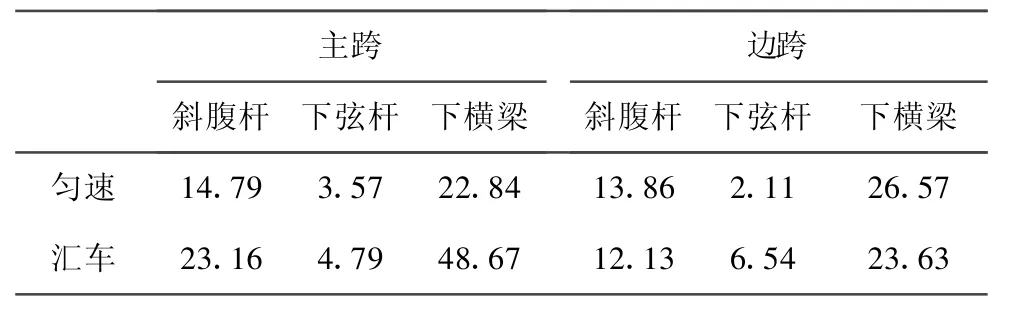
表2 斜拉桥Vonmises应力变化最大值计算结果/MPa

4 结语

该文通过精细有限元建模方法模拟桥梁构件空间位置、几何尺寸、材料特性、连接形式,得到了移动轻轨车辆与桥梁耦合振动下各构件准确、详尽的应力与变形结果。采用基于接触均衡分区的并行计算方法在上海超级计算机曙光4000A上进行计算,解决了模型较大造成的求解难题。通过分析可知,在各个构件中,下横梁所承受载荷最大,斜腹杆与下弦杆相连接的节点处为应力集中的部位,应力受到轻轨车辆的影响较大。

[1]邹锦华,王荣辉,魏德敏.城市轨道交通连续刚构桥车桥耦合动力分析[J].铁道科学与工程学报,2006,3(1):36-40.ZOU JIN-HUA,WANG RONG-HUI,WEI DE-MIN.Coupling dynamic analysis of vehicle/bridgEof urbanmass transit continuous rigid framEbridge[J].Journal of Railway SciencEand Engineering,2006,3(1):36-40.

[2]秦远田,陈国平,余岭,等.车-桥耦合系统动力学建模与响应分析[J].应用力学学报,2008,25(1):130-133.QIN YUANTIAN,CHEN GUOPING,YU LING,et al.Modeling and responsEanalysis of coupled vehiclebridgEsystem[J].ChinesEJournal of Appliedmechanics,2008,25(1):130-133.

[3]MAGDY SAMAAN,JOHN B.Kennedy,Khaled Sennah.Dynamic analysis of curved continuousmultiplebox girder bridges[J].Journal of BridgEEngineering,2007,12(2):184-193.

[4]MICHALmAJKA,MICHAEL HARTNETT.Effects of speed,load and damping on thEdynamic responsEof railway bridges and vehicles[J].Computers and Structures,2007,86(6):556-572.

[5]BRUNO D,GRECO F,LONETTI P.Dynamic impact analysis of long span cable-stayed bridges undermoving loads[J].Engineering Structures,2008,30(4):1160-1177.

[6]岳祖润,周宏业.一种铁路车桥耦合振动三维仿真的实现[J].铁道学报,2005,27(3):62-69.YUEZU-RUN,ZHOU HONG-YE.A simulation on 3D coupled railway vehicle-bridgEvibration[J].Journal of thEChina Railway Society,2005,27(3):62-69.

[7]FREIREAm S,NEGRAO J H O,LOPESA V.Geometrical nonlinearities on thEstatic analysis of highly flexiblEsteel cable-stayed bridges.Computer and Structures,2006,84(31):2128-2140.

[8]LESLAW K,HONGYI L,JERRY W,et al.FinitEelement analysis of vehicle–bridgeinteraction[J].FinitEElements in Analysis and Design,2006,42(12):950-959.

[9]彭俊,邓玮琳,周良,等.上海闵浦二桥主跨斜拉桥钢板桁组合梁设计[J].中国市政工程,2007(2):8-10.PENG JUN,DENG WEI-LIN,ZHOU LIANG,et al.Design of steel plate-truss compositEgirder on cablestayedminpu bridgEII,shanghai[J].Chinamunicipal Engineering,2007(2):8-10.

[10]JOHN O HALLQUIST.LS-DYNA theoreticalmanual[m ]. LivermorESoftwarETechnology Corporation,2006.

[11]ZHONG Z H.FinitEelement procedures for compactimpact problems.Oxford University Press,1993.

[12]刘青昆,归丽忠,舒继武,等.区域分解法解黑油数值模拟问题改进的并行计算[J].南京大学学报:自然科学版,2003,39(2):229-237.LIU QING-KUN,GUI LI-ZHONG,SHU JI-WU,et al.Improved Parallel Computing of Domain Decompositionmethods for Solving Numerical Simulation of BlackOil Reservoir[J].Journal of Nanjing University:Natural Sciences,2003,39(2):229-237.

[13]WANG X W,GUO L,GEW.Parallel implementation ofmacro-scalEpseudo-particlEsimulation for particlefilled systems[J].Computers and Chemical Engineering,2005,29:1543-1553.

[14]LANGER U.Boundary and finitEelement domain decompositionmethods[C]//Numericalmathematics and Advanced Applications:Proceedings of ENUMATH 2007,the7th European Conferenceon Numericalmathematics and Advanced Applications,Graz,Austria,September 2007.

[15]金先龙,李渊印.结构动力学并行计算方法及应用[M].北京:国防工业出版社,2008:138-139.