基于遗传算法的无源滤波器参数的优化

2010-08-10丁龙祥

船电技术 2010年9期

丁龙祥

(江苏海事职业技术学院，南京 211170 )

1 引言

无源滤波器是静止型无功补偿器的重要组成部分［5］，它主要作用是滤除电网谐波及补偿无功。本文以单调谐滤波器和高通滤波器作为参数调节的研究对象。

传统的遗传算法一般用来解决单目标、无约束的问题。缺点有：基本遗传算法在解空间进行随机搜索寻找最优解，而非确定性的迭代求解，遗传和变异的完全随机性虽保证了进化的搜索功能，但也使得一些好的优良个体被过早破坏。从过程来看，其初始解的产生、繁殖、变异都是随机完成的。遗传算法依靠产生大量的个体进行适者生存选择而逐步逼近最优解，这种完全随机化的过程虽然可以在整体上保证了进化，但却是一个漫长、随机的过程，计算效率低。另外遗传算法的选择算子、杂交算子的寻优功能随进化迭代次数的增加而逐渐减弱，在应用中常出现早熟收敛现象。当某一局部最优解和全局最优解较为接近时，个体之间的差别不大，多样性减少，搜索区域不断减少而导致结果落入局部最优。因此，要解决无源滤波器的多目标优化设计问题，在算法上必须作一定的改进。

2 遗传算法的改进

作为遗传算法重要的遗传参数的交叉概率 Pc和变异概率Pm。其最佳取值随具体应用、种群分布和遗传进化而变化；Pc、Pm取值固定是 SGA易早熟收敛和搜索效率较低的重要原因，这里引入自适应交叉概率和变异概率可较好地解决该问题。

用不同的方法对自适应遗传算法做改进，它既考虑解的全局性又考虑解的收敛性，取值如下：

式中 k为迭代次数；为交叉概率的初值；为交叉概率末值；gmax为最大允许的迭代次数。这样交叉概率就会随迭代次数增加而减小，从而避免上述问题。但是没有考虑到概率的变化同适应度函数的关系。而适应度函数值才是衡量性能指标的重要参数。

为此，本文对上述自适应遗传算法加以改进，

具体如下：

式中： fmax—代表群体中最大的适应度值

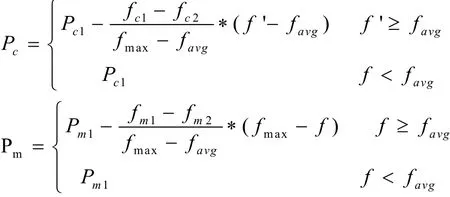
favg—每代群体的平均适应度值；f/—要交叉的两个个体中较大的适应度值；f—要变异个体的适应度值。

其中 PC1=0.9，PC2=0.6，Pm1= 0.1，Pm2=0.001

在改进的自适应遗传算法中，相应地提高了群体中表现优良的个体的交叉率和变异率，使得它们不会处于一种近似停滞不变的状态。为了保证每一代中的优良个体不被破坏，采用最优个体保存方法，使它们直接复制到下一代中。

3 无源滤波器设计原则和方案

3.1 无源滤波器设计原则

在实际应用中，一般是根据电网的谐波状况来确定无源滤波器的类型和组数［2］，如谐波源为带阻感负载的三相全控整流桥［4］，其特征谐波为6k±1（k为自然数）次，则应装设5，7次单调谐滤波器和二阶高通滤波器各一组。无源滤波器参数的设计应遵循以下原则：

（1）电容、电感、电阻之间的关系满足系统无源滤波器的滤波原理；

（2）无源滤波器的整体基波等效阻抗满足系统无功补偿的要求；

（3）无源滤波器的整体阻抗不应与电网阻抗形成串、并联谐振；

（4）装设无源滤波器后的电网谐波含量低于国家标准；

（5）各组无源滤波器谐波容量的计算不仅要包含各自所滤除的谐波容量，还要加上10%的背景谐波容量。

3.2 优化问题方案

在以上原则的基础上，进行无源滤波器参数的优化设计［1］，还必须考虑三个问题。

（1）装设无源滤波器的初期投资最小；

（2）无源滤波器的装设既不能使系统出现无功功率过补偿现象又要使系统的功率因数尽量接近1；

（3）无源滤波器的装设要使电网谐波含量在低于国家标准的基础上，越低越好。为了分析的方便与统一，谐波电压、电流含量均以总畸变为衡量标准，即TV和TI式中Tv、T1分别为电压、电流的总畸变率；V1，I1为基波电压和电流；Vh1，Ih1为第i次谐波电压和电流；Tvmax，I1max分别为电压、电流总畸变的上限一般根据国家标准计算。

因此，无源滤波器参数的优化设计问题，就是要满足上述约束条件，这里采用一种改进的混沌遗传算法来解决这个多目标优化问题。

4 具体计算实例

某轧钢厂母线的主要谐波源是4台整流变压器［4］，实测电网谐波电流如表1 所示，因此特征谐波的次数为5，7，11次。系统的平均功率因数cosφ1为 0.75，设计后的平均功率因数 cosφ2为0.92。因此，所需无功功率可由式计算：

Q = P(tanφ2--tanφ1)

配电网在装设滤波器组前，各次主要谐波电流如表所示。由表 1中可知5次，7次。11次谐波电流值较大，其中5次谐波电流严重超标。由表2的各次谐波电流允许值及综合考虑应该补偿的无功功率和各次谐波含有率，决定在配电网中装设5次，7次，11次单调谐滤波器和高次滤波器。

为使滤波器满足谐波指标和无功补偿的要求，用上述方法对滤波器进行优化，以装设一组高通滤波器。在单调谐滤波器设计中，LC参数的选择会影响滤波效果，特别是当电网频率或LC参数发生漂移时的滤波效果，因此需要选择最佳的品质因数Q，以保证滤波器对频率的选择性和滤波器在频漂及参数漂移下的滤波效果。在高通滤波器设计中，各参数的恰当配合，可大大改善滤波器效果并减小其有功损耗。在此引入了一个与品质因数相关的参数m，其中m=L/R2C，通过品质因数Q和m，可以建立滤波器中的电感，电容及电阻的关系。因此，选择各滤波支路的电容量C5C7C11优化的独立变量。对于兼作无功补偿的滤波器，应使滤波器组补偿的无功总量与系统的要求一致，对优化设计的结果采用了性能评价，即在配电网中加装无源滤波器组后，电网总谐波电压畸变率最小为优化目标［3］。

表1 滤波前测得各次主要谐波电流

表2 各次谐波电流允许值

1）染色体编码

染色体代表解的形式，包含所有的遗传信息，本文根据无源滤波器设计原则来构成染色体的基因链，采用实数制编码，对于单调谐滤波器有

这里以二阶高通滤波器为例，有

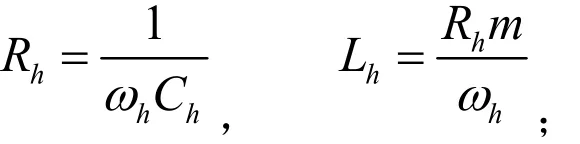
式中ωs，Ls，Cs, Rs和Q分别为单调谐滤波器的谐振频率、电感值、电容值、电阻值和调谐锐度；ωh，Lh，Ch, Rh，m分别为二阶高通滤波器所对应的截止频率、电感、电容、电阻和调谐值。ωs，ωh是由谐波源的特征谐波确定的常数，所以每组无源滤波器的各个参数均可由电阻和电感两个参数来表示，因此，染色体可表示为一个2n维的基因链。

式中，n为无源滤波器的组数（这里5次、7次、11次滤波器和高通滤波器）。

2）适应度函数

根据优化目标，构造如下适应度函数：

式中 C是一个较大的正数，用来保证F2(X)为正值，其值可以根据实际情况确定；α和β大于零的常数，用来匹配电压、电流畸变率的权重，一般α:β=1:10。

3）结果

各参数结果如表3 所示，表4为安装滤波器后测得的各次主要谐波电流。对比表1和表2发现各主要次谐波畸变（5次、7次、11次等）在装设滤波器后都有了明显改善，同时由实测可知配电网的功率因数在系统满载时也保持在 0.9以上。以上结果说明把遗传算法应用于滤波器的设计不仅可以得到令人满意的结果，同时还大大减小了人工的计算量，而且明显提高了算法的寻优速度。