一种基于身份的Ad hoc组密钥管理方案
2010-08-07王猛徐平鸽顾维娜淮北煤炭师范学院计算机科学与技术学院安徽235000
王猛 徐平鸽 顾维娜淮北煤炭师范学院计算机科学与技术学院 安徽 235000
0 引言
Ad hoc网络是由一组带有无线收发器的无线节点或移动终端相互协作形成的一种新型网络,它独立于固定的基础设施,采用分布式技术管理,可以做到快速配置和自组织网络。由于其具有有限的资源、多跳的通信和动态的网络拓扑结构等特点,将会受到更多的安全威胁。所以在无线Ad hoc网络中,必须利用密码学理论与技术来有效地防范潜在的攻击,而密码理论与技术在实际使用中的安全性,则主要依赖于密钥管理的安全性。一般来讲,根据Ad hoc网络自身的特点,一般要求节点的密钥能动态生成且不依赖任何固定的第三方(TTP),并确保密钥在传输中的安全,同时具有较小的计算量、存储量和通信量。
早在1984年,第一个公钥密码系统RSA的合作发明者之一Shamir为了简化传统的PKI公钥体系架构中CA对各用户证书的管理,首次提出了基于身份的密码学(IBC)的思想,其基本的想法就是将用户的身份与其公钥捆绑在一起,用户的身份信息即为用户的公钥。但是基于身份的加密算法(IBE)长期都没有得到有效的解决方法。2001年,Boneh和Franklin通过使用一个定义在椭圆曲线上的双线性映射,提出了一个非常实用的IBE方案,并且给出了严格的安全性证明。在基于身份的密码体制中,任何人都可以根据用户的身份计算出他的公钥,而私钥则是有可信的中心生成的,这种密码体制的优点在于:①获取公钥只需要很少的计算量和通讯量;②不使用证书;③可以通过在公钥中增加时间戳来完成公钥的撤销。所以,基于身份的密码体制在资源有限的Ad hoc网络中使用具有一定的优势。
组密钥是所有组内成员之间相互协作,共同生成一个组密钥,组外的成员不能计算出该密钥,用以对组内节点间数据传递进行加密、解密和认证等操作,以满足数据机密性和完整性等安全需求。
本文提出 Ad hoc网络中一种新的基于身份的组密钥管理方案,该方案的安全性建立在椭圆曲线上双线性对的求解难题,并且结合组密钥的最新研究成果,方案所需的开销更小,安全性和效率更高,轮数少,算法简单。
1 基本理论知识简介
1.1 基于身份的密码体制和双线性对
双线性对最初是用于密码攻击,被认为是对密码体系不利的,比如用Weil对的MOV攻击将超奇异椭圆曲线或超椭圆曲线上的离散对数问题归约为有限域上的离散对数问题,这使得超椭圆曲线不能作为密码体系。但是,近年来发现了双线性对在密码学上的积极作用,2000年Joux做出其突破性的工作,他提出了一个基于超奇异椭圆曲线上的双线性对的基于身份的Deffie-Hellman密钥协商协议。此后双线性对的许多应用相继被给出,其中最值得注意的有两个:一个是Boneh和Franklin的基于双线性对的基于身份的密码方案,这是第一个高效且可证明安全的基于身份的密码方案;另一个是Boneh、Lynn和Shacham提出的基于双线性对的签名方案,这个方案是签名最短的签名方案。双线性的定义如下:
设G1和G1分别是阶数为素数q的加法群和乘法群,P为G1的一个生成元。假设G1和G1这两个群中的离散对数问题都是困难问题。双线性映射e:G1×G1→G2具有如下特征:
(1) 双线性:对于所有的 P,Q,,R∈G1和所有的 a,b∈,

(2) 非退化性:存在P,Q∈G1,满足e(P,Q)≠ 1;
(3) 可计算性:对所有的 P,Q∈G1,e(P,Q)可以在多项式时间有效计算出来。
当q是个素数时,G1中任意一个元素P都是生成元,由非退化性和双线性,e(P,P)也是G2中的生成元。
我们可以在具有以上性质的群 G1上,定义如下的密码问题:
(1) 离散对数问题(DLP):给定P,aP,计算a∈Zq。
(2) 计算Diffie-Hellman问题(CDHP):给定P,aP,bP,计算abP。
(3) 决策Diffie-Hellman问题(DDHP):给定P,aP,bP,cP,判断是否c=abmodq。
(4) Gap Diffie-Hellman问题(GDHP):在群 G1中,当DDHP计算容易,但 CDHP计算困难时,称群 G1为 Gap Diffie-Hellman群。
1.2 组密钥管理机制
组密钥管理是指组内成员共同协商生成、分发和更新组密钥。其基本任务是:为合法的组内成员分配和维护密钥,实现组播通信时秘密信息在合法组成员间共享,而非组成员无法知道该秘密信息。同时,利用组密钥对组播内容进行加密,确保得到的通信数据的节点是组内成员,从而在确保数据机密性的同时达到一定程度上的数据源认证。
第一个组密钥协商协议是ING协议,之后,学者们提出了许许多多的组密钥协商协议,下面简单介绍一下Du的俩轮密钥协商协议。
2003年,Du等人讲椭圆曲线密码体制应用于BD协议,改进并使之适用于基于身份的加密体系中。Du等人方案的安全性建立在椭圆曲线双线性对以及 BDH假设之下,其过程可以简单表述如下:
首先,系统建立双线性对以及 BDH假设的环境,发布参 数{G1,G2,p,P,Ppub,H,H1}。 设 定 节 点IDi的 公 钥 为Qi=H1(IDi),其私钥为 Si=sQi。然后各个节点执行如下步骤:
(1) 节点IDi,1≤i≤n,选择密钥Ni∈Zq,计算并广播zi=NiP,Ti=H(zi)Si+NiPpub。
(2) 节点IDi验证然后广播
(3) 每个节点IDi计算回话密钥:
最终每个节点都将得到相同的会话密钥K=e(P,P)(N1N2+N2N3+,…Nn N1)s。
和BD协议相比,Du的协议采用了椭圆曲线密码体制以及双线性配对,每个节点只需进行常数次双线性配对和椭圆曲线计算,有效降低了计算量。其次,由于与基于身份的加密体制的结合,使之更加适用于Ad hoc网络和更具有安全性。
2 新的基于身份的组密钥管理方案
2.1 系统建立和组密钥生成
假设Ad hoc网络中有K个用户,即U1,U2,…,UK,其身份IDi用M1,M2,…,Mk来表示,并且假设节点已经有了自己的公私钥。随机根据路由最优、节点权重最大和跳数最少的原则选择产生一个组首,记为Mn。我们可以设Gi=H(Mi)为节点i的公钥。
(1) 系统初始化时,每一个组内成员随机选择一个随机数ri∈,并且计算以下四个参数:
(2) 其他组成员收到每个节点的广播后,对收到的数据及其签名进行验证,
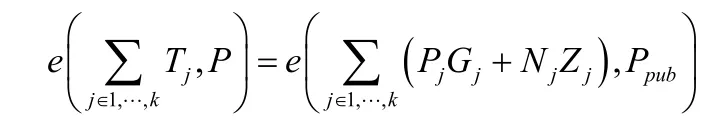

(3) 组首节点nM 验证每个节点计算的ki是否相等,如果相等,则ki为系统初始时的组密钥。
如果上述等式成立,则根据如下方法计算ki。
2.2 成员加入时的组密钥更新
当组外的成员Mk+1加入群组之前,需要首先根据自己的ID产生公私钥对和签名,并且向组内广播自己的信息和身份IDk+1,组内的Mn发起组密钥的更新。k+1个组内成员重复系统建立时的运算,最后由 Mn计算和收集验证组密钥 ki:
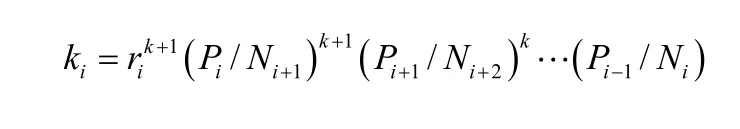
2.3 成员离开时的组密钥更新
成员离开群组后,首先根据规则在剩余的组成员集合中选择合适的成员为组首节点Mn,然后由组首节点发起组密钥的更新运算。运算步骤和2.2节加入节点时类似,只是最后一步需要稍微变化:

3 安全性分析
(1) 密钥的安全性:本方案中的组密钥每次更新时,都随机选择一个数 ri∈,协商生成新密钥,因此一次会话密钥的泄露并不会影响到其他的密钥。
(2) 前向安全性:离开群组的节点不能继续参与组播,而根据以往的密钥协商信息不能计算出新的组密钥,即无法利用它所知道的密钥解密后续的加密数据。
(3) 后向安全性:新成员加入群组后,新加入的成员无法用其新获得密钥解密之前的秘密数据。
4 性能比较分析
本方案和Du方案相比,在性能上如表1所示。

表1 性能分析
由表可知,本方案较之Du的方案节点的双线性配对运算相同,但生成组密钥时只需要一轮运算,且每个节点只要组播一次,即组播次数为n次,综上,该方案的总体性能良好。
5 结束语
本文提出了一种新的基于身份的Ad hoc网络中组密钥管理方案,包括系统建立时的初始化、节点加入时的组密钥更新和节点离开时的组密钥更新等三个操作。和现有的密钥管理相比,它提供更高的安全性,同时保证更好的运行效率,利用基于身份的密码体制可以减少系统的计算、存储和通信开销,因此,本方案比较适合于Ad hoc网络环境中。
[1] A.Shamir.Identity-based Cryptosystems and Signatures Schemes.CRYPTO 1984.
[2] D Boneh, M Franklin. Identity-based Encryption from the Weil pairing [A]. Proc of Crypto 2001[C],LNCS 2139,Springer-Verlag.2001.
[3] 况晓辉,胡华平,卢锡城.移动自组网络组密钥管理框架[J].计算机研究与发展.2004.
[4] 徐倩,张福泰,刘志高.无线Ad Hoc网络中基于身份的密钥管理方案[J].南京师范大学学报.2006.
[5] 张金颖,邓子健.基于身份的密钥协商方案[J].信息安全与通信保密.2007.
[6] 郭现峰.TTS组密钥协商协议的安全性分析与改进[J].计算机工程与应用.2008.
[7] 王育民,刘建伟.通讯网络的安全理论与技术[M].西安电子科技大学出版社.1999.
