一种改进的混合遗传聚类算法的数据挖掘技术
2010-08-07崔志刚
崔志刚
武汉大学软件工程国家重点实验室 湖北 430063
0 引言
数据挖掘(Data Mining)就是从大量数据中获取有效的、新颖的、潜在有用的、最终可理解的模式的非平凡过程。在庞大的数据集合中存在相似性很强的数据集,如果能将数据集进行分类,依据相似性建立一个种群,使得数据挖掘更有目的性和针对性。K-means聚类算法是一种快速有效的分类方法,具有较快的分类速度,但必须手动确定初始聚类中心,因此,若能够利用算法求得初始聚类中心,则结合K一均值聚类算法可以实现自动分类。遗传算法(Genetic A1gorithm—GA)是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是一种启发式的全局优化搜索算法,其简单通用,鲁棒性强,适于并行处理,应用范围广。遗传聚类是将GA应用于聚类的一种方法,其基本思想是通过遗传学习,将上一代的优良特性保留下来,并通过个体之间的基因组合、变异从而产生更为优良的下一代个体,这样经过数代的个体进化,最终找到满意的个体。鉴此,本文采用K-means算法进行聚类,并采用遗传聚类算法确定聚类中心,实例结果验证了改进的算法有效可行。
1 K-means聚类算法
在聚类算法中需要考虑到底聚类算法到什么时候终止,即是如何确定聚类中心,确定多少聚类中心。K-means聚类将数据划分为n个模式,每个模式的维度为d,取其中的最小K组作为我们的聚类起点,定义如下:
令{xi,i=1,2,…,n}为模式n的集合。其中xij表示xi的第j个特征。定义i=1,2,…,n;k=1,2,…,K,

那么,数组W=[wij]就有属性如下
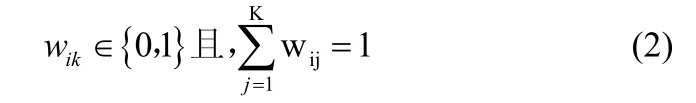
令第k个聚类中心族为ck=(ck1,ck2,…,ckd),那么
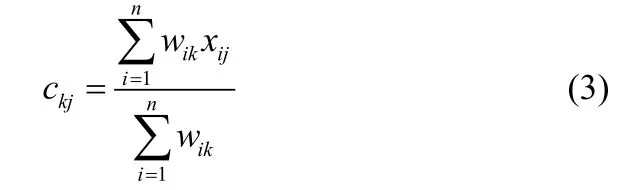
第k个族群的内联相关族群定义为
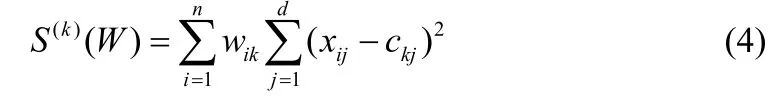
总的内联相关族群定义为
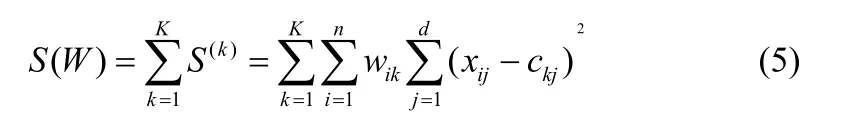
由此就可以找到W*=[w*ik]中的最小S(W),例如
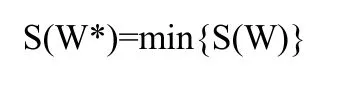
K-means算法是一个迭代算法,它开始于一个任意的族群,在每一次迭代的过程中确定那些模式属于同一聚类中心族模式,下一次的迭代就是取与该中心族相关的模式进行划分,该算法终止于没有一个模式可以在被重新指配给其它的聚类中心族。该算法由于初始的聚类中心选择的随机性,使得算法存在一个潜在的问题,及选择的聚类中心是否合适。
2 混合遗传聚类算法
遗传算法的主要问题是针对不同数据集的编码。通常采取自由选择的方法,在进化过程中生成:下一代的编码依据当前这一代的编码而不同。下面就关于编码及初始化及遗传运算做进一步的阐述。
2.1 编码
遗传算法的染色体编码有很多种,本文中采用较常用的是基于聚类中心的浮点数编码和基于聚类划分的整数编码。由于内联相关族群S(W)通常具有多维性、数量大等特点,聚类问题的样本数目一般远大于其聚类数目,因此确定染色体的长度 n在{1,2,…,K}中取值,将各个类别的中心编码为染色体。例如对于一个类别为 4 的聚类问题,假设数据集为2维。初始的4个聚类中心点为(1,3),(2,4),(6,9),(8,7),则染色体编码为(1, 3,2, 4,6, 9, 8, 7)。这种基于聚类中心的编码方式缩短了染色体的长度,提高了遗传算法的速度,对于求解大量数据的复杂聚类问题效果较好。
2.2 初始
第一代的初始聚类中心 P(0)是在集合{1,2,…,K}中随机选择的。基于此种选择算法可以在运行到选择某些族群为空概率为非零的匹配族群的时候停止,由于随机选择初始聚类族群以及其他族群可以围绕此聚类中心进行计算,使得p达到一个较为理想的赋值。
2.3 选择
根据适者生存原则选择下一代的个体。在选择时,以适应度为选择原则。适应度准则体现了适者生存,不适应者淘汰的自然法则。
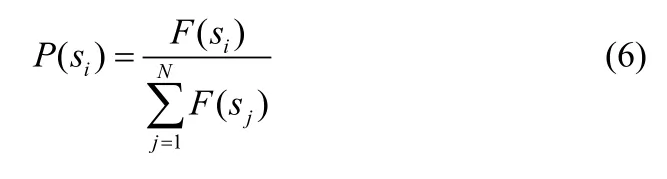
其中 F(Si)表示串 Si的合适的取值并且确定下一次变异的取值。本文采用轮盘赌的原则随机的选择。显然,从式(6)可知:①适应度较高的个体,繁殖下一代的数目较多。②适应度较小的个体,繁殖下一代的数目较少;甚至被淘汰。这样,就产生了对环境适应能力较强的后代。对于问题求解角度来讲,就是选择出和最优解较接近的中间解。
2.4 交叉
交叉从相互关联的数据源中,根据不同的聚类中心的距离,按照某种关系交叉其中的基因从而形成新的个体。为了从依存对象 xi中找到适应的等位基因 sw(i),令 dj=d(xi,cj)为xi与cj的欧氏距离,所以等位基因可以依据下面的公式选择
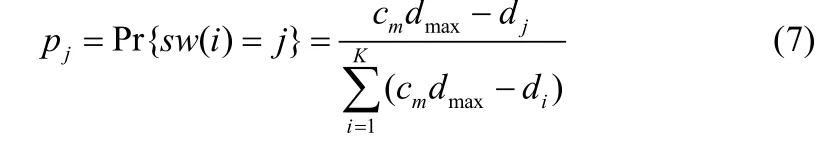
其中cm≥1并且dmax=maxj{dj}。
3 改进的混合遗传聚类算法
新群体的编码值为中心在变异后产生,将每个数据点分配到最近的类,形成新的聚类划分。按照新的聚类划分,计算新第二代的聚类中心,取代原来的编码值。 因为K -means算法具有较强的局部搜索能力,因此引入K-means操作后,可以大大提高遗传算法的收敛速度。
混合遗传聚类算法主要是改进了初始模板的选定方法。以每个向量为圆心,以向量空间中所有句子之间距离的平均值为半径作圆,然后根据每个圆内的数据点的密度来排序确定初始聚类中心和初始聚类数。 这样,K-means聚类算法需要的初始模板就由以上算法动态生成,而无需用户进行事先指定。整个过程包括以下几个基本步骤:
步骤1:选取两个正数,一般R2 =2R1 ,其中R1为距离矩阵W(i,j)中所有元素之间距离的平均值。
步骤2:以每个句子为圆心,以R1为半径作圆,计算落在每个圆内的数据元素数目,即样本密度。
步骤 3:将样本密度按从大到小的顺序排列,取密度最大者作为第一个凝聚点Z1 ,在密度次大的单元中任选一点k,若与第一凝聚点之间距离大于R2,即 |Z1 -k|> R2,则把k 作为第二个凝聚点Z2 ,否则继续判定下一密度最大者,若下一密度最大者中的任一点与前面若干个凝聚点之间距离均大于R2,则将之作为又一新的凝聚点,如此反复迭代直到没有新的凝聚点生成。
步骤 4:这些凝聚点作为聚类模板的初值即分类个数 k以及初始k个聚类中心Z1,Z2, Z3,.......,Z k。
步骤5:把得到的k和k个聚类中心Z1,Z2,Z3,.......,Zk 作为k - means 算法的初始模板,继续用k-means算法迭代,最后得到k个聚类。
经过以上步骤的初始分类,可以得到整个向量空间的分类个数 k 以及模板初始聚类中心 Z={ Z1,Z2,Z3,.......,Zk },这样我们就从整个向量空间的统计信息中自动确定了聚类所需要的初始聚类数目和初始聚类中心,为后面的聚类过程打下了一个较好的基础。
在确定k和聚类中心Z后,接下来对数据元素向量空间进行k-means 迭代。其基本原理是根据所有向量与聚类中心距离的远近程度,形成k个互不相交的聚类,较为相似的句子都聚在同一类中。因此自动聚出来的这些自然的类可以被看成描述不同侧面的理想信息,用于区分及表达不同的类。
4 实例
本文选择从网络下载的语料,选用其中的 1000篇,利用手工进行分类,分类结果如表1。

表1 网络预料手工分类结果
衡量信息检索性能的召回率和精度也是衡量分类算法效果的常用指标。但是聚类过程中的分类类别与手工分类类别不存在确定的一一对应关系,因此直接以精度和召回率作为评价标准是不可取的。为此本文选择了平均准确率作为评价的标准。平均准确率是通过考察任意两篇文章之间类属关系是否一致从而来评价聚类的效果。实验中分别采用传统的K-means算法与改进算法,比较如表2。

表2 K-means算法与混合遗传聚类算法比较
实验结果表明改进与传统的K-means算法在运行速度上有一定的提高,平均准确率普遍要好,特别是在正确的指定聚类中心数K时,平均准确率提高了约9%,由此可以看到改进算法具有一定的优势。由于使用的文本集文本数量较小,未来还会继续在更大规模的文本集上测试改进算法。
另外,分别用本文所描述的改进方法和传统K-means聚类算法进行聚类确定文档集合的子主题数,并人工确定每个主题文档集合中包括的子主题数。其中,在采用传统K-means聚类方法时,初始聚类数目和初始聚类中心是需要人为给定的(取句子总数的 10%)。本文分别将改进算法以及传统K-means算法得到的子主题数列出如3表所示。
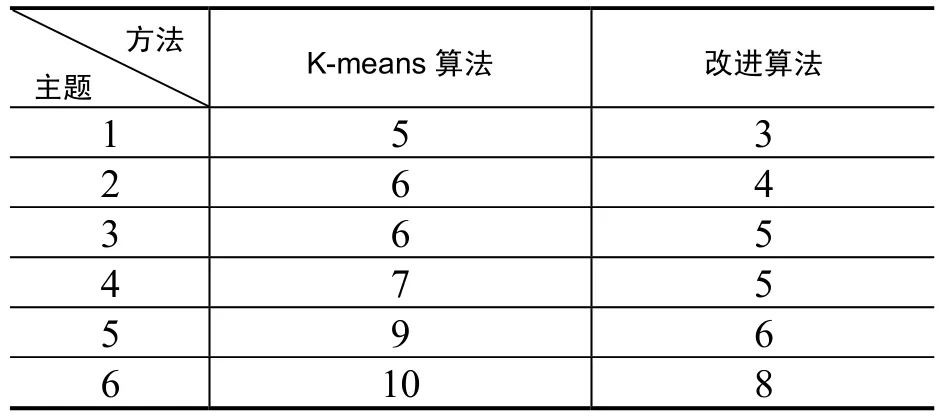
表3 K-means算法与改进算法子主题数确定的比较
从上表中可以看出,改进的混合遗传聚类算法得到的子主题数比较接近,这表明通过文中的方法在发现文档集合中的潜在子主题时比较符合文档的客观情况,而通过人为主观经验得到的子主题数相对较大。综上所述,通过改进的混合遗传聚类算法自适应发现的子主题数比较能客观的反映文档集合的情况,具有一定的效果。
5 结语
本文对数据挖掘中聚类算法做了详细的分析,对于不同的聚类方法中所出现的人工确定聚类中心点问题做了改进。本文详细分析了K-means聚类算法,在此基础上对于聚类中心点选择遗传算法通过交叉变异自适应的方式选取,构造向量间的距离矩阵,计算中心点。通过实验分析,发现改进的聚类算法有一定的效果。
[1] 申锐.数据挖掘技术中聚类算法的探索与研究[J].山西科技.2009.
[2] 张翠萍,杨善超.基于K-均值聚类算法的中药叶片显微图像分割[J].石河子大学学报(自然科学版).2009.
[3] 范明译.JiaweiHan Micheline Kamber.Data Mining:Concepts and Techniques[M].北京:机械工业出版社.2001.
[4] 唐西西.一种新的混合遗传聚类算法[J].广西工学院学报.2006.
