基于JADE算法的盲DOA估计
2010-08-06赵佳杨景曙金家保
赵佳,杨景曙,金家保
(电子工程学院 信息对抗研究所,安徽 合肥 230037)
1 引言
在实际环境中多径现象是普遍存在的,如在雷达测高或低角跟踪的应用中,目标直接回波与地面反射波是强相关或相干的,类似的例子还有通信中基站与移动台之间的信号传输。此时,若干强相关或相干的信源会合并成一个信源使信号子空间秩亏损,故不能通过一般的 DOA估计方法(如MUSIC、ESPRIT等)对信源进行分辨或测向。现有处理方法主要分为2大类[1]:降维处理和非降维处理。降维类(如空间平滑类算法)方法[2~4]较为简单,但阵列孔径损失较大;非降维类(如Toeplitz近似算法)方法[5,6]虽不损失阵列孔径,但稳定性较差,估计偏差大。在实际环境中,由于无线信道传播环境的复杂性,入射到天线阵列的信号中可能存在同向信号;此外,由于多径相干信号的存在,还容易导致过载现象,即天线阵收到的信号数大于阵元数。在这种情况下,现有的这些解相干类 DOA估计方法都不能有效地进行DOA估计。因此,有必要探索新的DOA估计方法。
盲源分离技术是在源信号信息及混合过程都未知的情况下,仅对观测信号进行处理就可以实现对源信号和系统的辨识,在被动目标的检测与估计中具有优势。因此,这里考虑将盲源分离技术应用到 DOA估计中。独立分量分析(ICA, independent component analysis)是近年来由盲源分离技术发展起来的多道信号处理方法,在语音识别、通信、图像处理、医学信号处理等领域受到了广泛的关注。JADE算法[7]是由Cardoso提出的一种基于矩阵联合对角化的ICA方法。该算法的主要特点是加强了算法的代数概念——引入了多变量数据的四维累积量矩阵,并对其作特征分解,简化了算法,也提高了结果的稳健性。
本文提出了一种基于JADE算法的DOA估计新方法。该方法是利用JADE算法对阵列流型矩阵进行盲辨识,并将该阵列流型中的方向矢量看成是由多路复正弦信号线性混合而成,进而利用频谱分析的方法对各信源进行DOA估计。经过仿真验证,新方法不仅可以实现对来波方位相同信号的分辨,且具有较好的稳定性,在信源数大于阵元数时仍然可以使用。
2 相干信号源的数学模型
窄带阵列信号处理的模型如下:

其中,A为阵列流型;s(t)是信号矢量;n(t)是加性高斯噪声矢量。

其中,天线阵列的阵元数为M,接收的信号数为N,第i路信号的波达方向(DOA)为iθ。
若 s1(t)和 s2(t)是由同一源发射经不同路径传输到天线的强相关或相干信号,则有 s2( t) = αs1( t),其中,α为复数幅度因子,表征了2个信号间的增益和相位关系。此时,信号模型中阵列流型式和信号矢量式可写为

其中,混合信号1()t′s的来波方向既不是1θ也不是2θ。
3 基于JADE算法的DOA估计
假设信号模型中源信号各成分1s(t)之间互不相关,且均值为零,则其协方差阵为
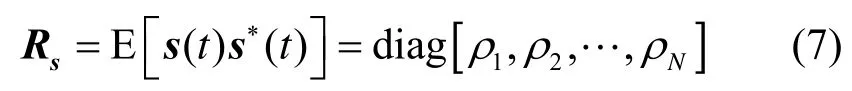
那么,天线接收信号中的信号部分y(t)的自相关矩阵为
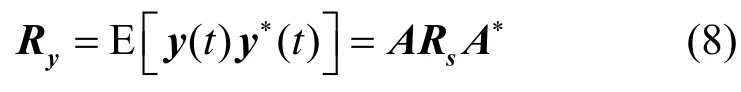
假设加性噪声 n(t)为归一化白噪声,与信号相互独立,则
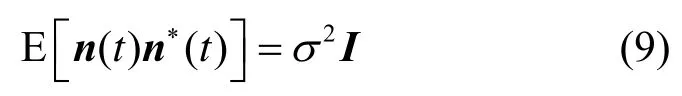
在上面2个假设的前提下,阵列观察信号的协方差阵可以写为

3.1 球化数据
球化是JADE方法的第一步,通过球化可以消除各通道数据间的二阶相关。假设N×M维球化矩阵为W,则球化就是使输出 z =Wy的各分量 zi(t)的方差为1,且互不相关(但未必相互独立)。
不失一般性,可以假设各源信号方差都为 1,则

所以
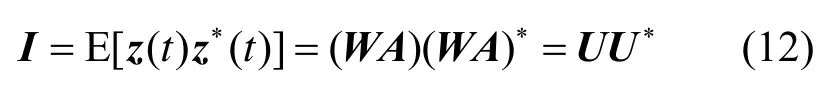
其中U=WA是一个酉矩阵。对任意的球化矩阵W都存在一个酉矩阵使得

其中,#表示伪逆,W#=W*( WW*)-1。
3.2 JADE算法
由式(13)可知:求出酉矩阵U便可对阵列流型矩阵A实现辨识。JADE算法的主要特点是引入了四阶累积量矩阵。令为球化后的天线阵观测矢量,M为任意M×M矩阵。则z的四阶累积量矩阵第 i, j个元素定义为其中,Kijkl(z)是矢量z中第 i, j, k, l 4个分量的四阶累积量, mkl是矩阵M的第 k, l个元素。
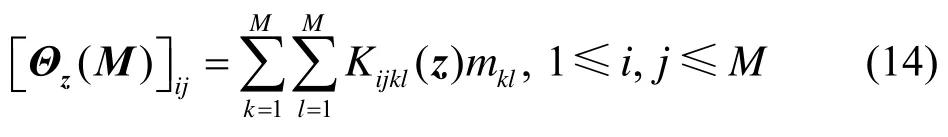
酉矩阵U = W A=[u1u2…uM],ui=[ui1ui2…uiM]T,则
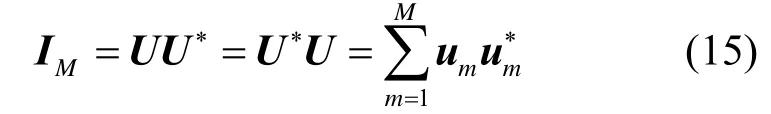
可以证明[7]:以M为权重矩阵构成的累积量矩阵 Θz( M)必可分解为

其中,λ= k4(sm)是信源 sm的峰度,M称为 Θz(M)的特征矩阵,k4(sm)是对应的特征值。因此 Θz(M)可表示成 U Λ(M) U*。
其中

由此可见,U矩阵在这里起着将 Θz(M)对角化的作用。如果各信源的峰度互不相同,则um和λm也就各不相同,那么就能得到酉矩阵U,进而可以求得阵列流型矩阵A和各独立分量。
3.3 DOA估计的实现
天线阵为均匀直线阵,阵元间距为d,则阵列流型矩阵中的的方向矢量可以看成是对复正弦曲线的均匀采样,采样数即天线阵元数M。例如:

其中

式(19)中,f为载波频率,c为波速。
复杂多径环境下,方向矢量可以看成是由多路复正弦曲线线性混合而成。
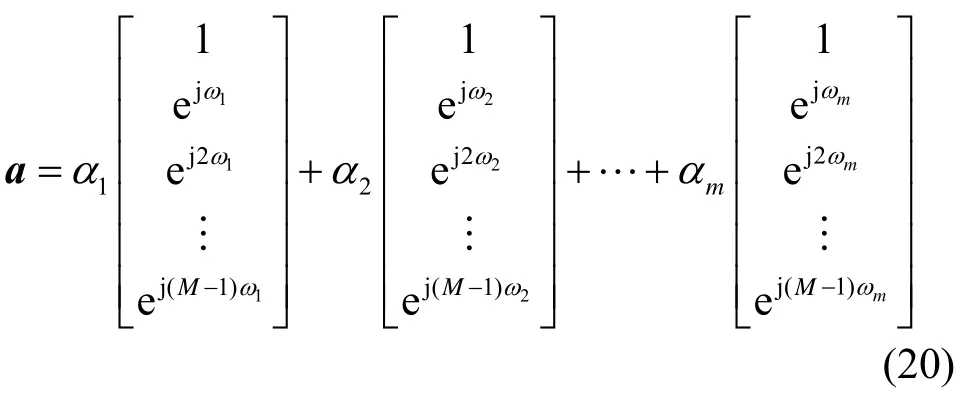
式(20)中iα为复常系数。
可以采用频谱分析的方法估计各频率点ωi( i=1 ,2,…,m ),进而可求出信号的来波方向。

频谱分析一般是通过DFT方法来实现,但在这里,由于天线阵元数有限即采样数据较少,不宜采用DFT方法,而是采用一些其他的方法,如改进的前后向预测算法MFBLP[9]等。
综上所述,基于JADE算法的DOA估计实现步骤总结如下。
第2步:选择矩阵组M,根据球化数据z求得一组累积量矩阵 Θz( Mi),i=1~P。
第5步:利用MFBLP算法对矩阵Aˆ的列矢量进行频率估计,进而计算出各信号来波方位为

这里称为JADE-MFBLP算法。
4 克拉美罗界
利用中心极限定理可知:具有确定均值和方差的多个独立随机过程的混合接近高斯分布。在盲源分离和独立分量分析中,一般假设各源信号是相互独立的,且为未知的非高斯分布(至多有一个高斯分布),而且假设混合过程是线性的,混合矩阵固定,且信号和噪声的均值为零,可以认为混合信号的分布近似为多元高斯分布。那么,混合信号概率密度函数的确定,只需要确定各混合信号的均值和方差。
由于信号间相互独立,信号和噪声互不相关,且均值都为零,则混合信号x的均值为

协方差矩阵为


那么,L次独立快拍数据的联合密度函数可以写为

由于假设多次快拍间是独立的,可以先对一次快拍进行处理,最后再将所有的结果组合。单次快拍的对数似然函数为

Fisher信息矩阵(FIM)中的元素为
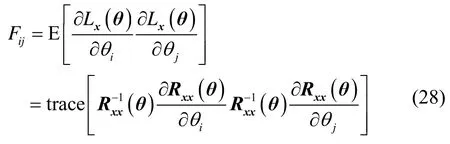
应用矩阵求逆引理:
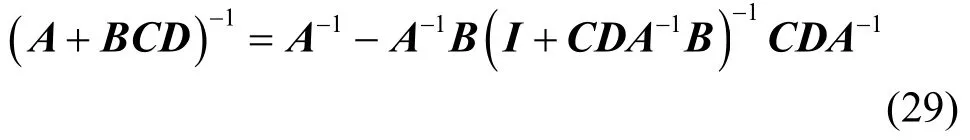
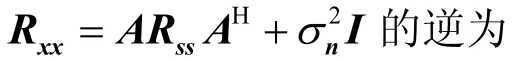

将FIM矩阵写为如下分块矩阵的形式。

可以按同样的方式将 CRB矩阵写成分块矩阵形式:

利用分块矩阵的求逆公式,可以求得[8]

上述的所有表达式都是基于单次快拍结果。如果有N次独立的快拍结果,那么它的对数似然函数为


5 仿真实验
本节将对DOA估计性能进行了仿真分析。
仿真1 2个独立信号源。
假设有2个相互独立的QAM信号,来波方位分别为θ1和θ2,信噪比为SNR,天线阵元数为M,采样长度为 NS= 1 000。
首先对 MUSIC算法、Toeplitz近似算法以及JADE-MFBLP算法在不同信噪比下的成功概率和估计方差进行仿真实验,实验结果如图1所示。
由图1可以看出,本文所提出的新方法在不同信噪比下对2个相互独立的信号进行来波方位估计时,估计方差较MUSIC算法和Toeplitz近似算法都要小;成功概率与Toeplitz近似算法基本相同,比MUSIC算法要好。
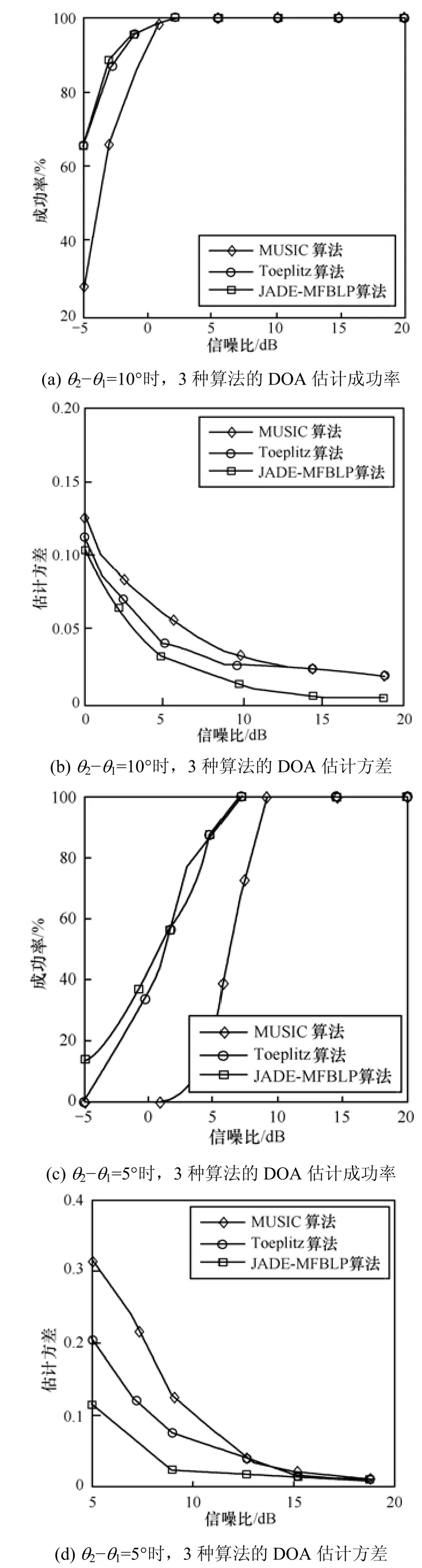
图1 MUSIC、Toeplitz近似算法和JADE-MFBLP算法对2个相互独立信号的估计性能信真结果
当2个信号的来波方位相同时,且未知任何信号先验知识的情况下,常用的 DOA估计方法(例如MUSIC算法、Toeplitz近似算法等)都是无法进行DOA估计的。而JADE-MFBLP算法仍然可以实现对这2个信号的有效DOA估计,实验结果如图2所示。
由图2可以看出,虽然JADE-MFBLP算法性能较2个信号来波方位不同时有所下降,但还是可以实现对2个来波方位相同信号的有效DOA估计。
下面对基于JADE盲源分离的DOA估计方法的估计方差与理想克拉美罗下界进行比较。此时,M= 8 ,仿真结果如图3所示。

图3 JADE-MFBLP算法的估计方差与CRB的比较

图4 JADE-MFBLP算法与JADE-Toeplitz算法随信噪比变化时的成功率和估计方差
由图3可以看出,JADE-MFBLP算法的的估计方差随着信噪比的增加,逐渐逼近理想的克拉美罗下界。
仿真2 2个相干信号源。
下面假设有2个完全相关(相干)的QAM信号,来波方位分别为θ1和θ2,信噪比为SNR,天线阵元数为M=8,采样长度为 NS= 1 000。由于MUSIC算法不能对相干信号进行有效DOA估计,因此这里只对Toeplitz近似算法以及JADE-MFBLP算法在不同信噪比下的成功率和估计方差进行仿真实验,实验结果如图4所示。
由图4可以看出,在对2个相干信号源进行DOA估计时,当信号来波方位相差较大时,Toeplitz近似算法的估计性能要略优于JADE-MFBLP算法;但当 2个信号来波方位较小时,Toeplitz近似算法的估计方差明显变大,性能下降,而JADE-MFBLP算法性能则明显优于Toeplitz近似算法。由此可见,JADE-MFBLP算法的稳定性要优于Toeplitz近似算法。
仿真3 JADE-MFBLP算法对多个相干信号的分辨能力。
JADE-MFBLP算法对相干信源的分辨能力与JADE算法的信号盲分离能力和 MFBLP算法的频率辨识能力密切相关。在不考虑噪声影响的情况下,JADE-MFBLP算法在不同阵元数时对相干信源的分辨能力如图5所示。
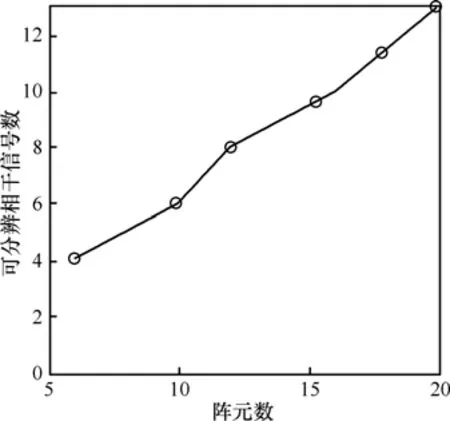
图5 不同阵元数时JADE-MFBLP算法可分辨的相干信源数
下面在阵元数M=6及不同信号源数的情况下,用JADE-MFBLP算法进行DOA估计。实验结果见表1(其中CM为常模信号)。
由图5可以看出,随着阵元数的增加,JADEMFBLP算法可分辨的相干信源数也增多。从表 1则可以看出,当源信号增多时,JADE-MFBLP算法的分辨效果受到一定的影响,但当天线阵接收信号数(含相干多径信号)大于阵元数时,仍可以实现对各信号有效的DOA估计。

表1 JADE-MFBLP算法对多个信号进行DOA估计
6 结束语
在复杂的电磁环境下,不仅可能存在同向信号,而且当多径现象存在时还会造成过载现象等,现有的DOA估计方法都不能很好解决这些问题。因此,针对上述问题,本文提出了一种基于 JADE算法的DOA估计新方法。仿真实验证明,该方法不仅对独立信号有较好的估计性能,可以实现对来波方位相同的2个信号实现有效分辨,而且在对相干信号进行分辨时的稳定性较Toeplitz近似算法要好,在信源数(含相干多径信号)大于阵元数时仍然可以使用。因此,在复杂的多径环境下,采用本文方法进行DOA估计将更具有优势。
[1] 王永良,陈辉,彭应宁. 空间谱估计理论与算法[M]. 北京∶ 清华大学出版社, 2004.WANG Y L, CHEN H, PENG Y L. The Theories and Algorithms on Spatial Spectrum Estimation[M]. Beijing∶ Tsinghua University Press, 2004.
[2] SHAN T J, WAX M, KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE ASSP, 1985,33(4)∶ 806-811.
[3] PILLAI S U, KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE ASSP, 1989, 37(1)∶ 8-15.
[4] DI A. Multiple sources location-a matrix decomposition approach[J].IEEE ASSP, 1985, 33(4)∶ 1086-1091.
[5] HAN F M, ZHANG X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas and Wireless Propagation Letters,2005, 4(1)∶ 1086-1091.
[6] 韩芳明, 张守宏. 用改进的MUSIC算法实现相干多径信号分离[J].系统工程与电子技术, 2004, 26(6)∶ 721-724.HAN M F, ZHANG S H. Separation of coherent multi-path signals with improved MUSIC algorithm[J]. Systems Engineering and Electronic, 2004, 26(6)∶ 721-724.
[7] PHAM D T, CARDOSO J. Blind separation of instantaneous mixtures of nonstationary sources[J]. IEEE Trans on Signal Processing, 2001,49(9)∶1837-1848.
[8] HARRY L, TREES V. Optimum Array Processing. Part IV of Detection, Estimation, and Modulation Theory[M]. John Wiley & Sons, Inc,2002. 704-720.
[9] TUFTS D W, KUMARESAN R. Estimation of frequencies of multiple sinusoids∶ making linear prediction perform like maximum likelihood[J]. IEEE Proc, 1982, 70(9)∶ 975-989.
