低复杂度上行多用户MIMO检测算法

黑永强，李晓辉，易克初，杨宏

（1. 西安电子科技大学 综合业务国家重点实验室，陕西 西安 710071；2. 中国空间技术研究院 总体部，北京 100094）

1 引言

与单用户MIMO系统相比，多用户MIMO系统能够获得更高无线信道容量。然而由于多个用户在相同的频带内同时进行通信，必然会存在多用户间的共道干扰(CCI)，因此如何有效消除 CCI将成为提高系统性能的关键所在。解决这一问题的一种有效方法是通过多用户检测[1,2]来完成，而目前提出的多用户检测算法主要有基于 Turbo迭代行多用户检测[3,4]算法，基于马尔可夫链蒙特卡洛多用户检测算法[5,6]以及采用凸优化求解多用户检测[7,8]算法等。近年来，结合空时处理和空时编码的新型多用户检测技术[9～11]已引起学者广泛的关注，其原因在于空时处理可以在有效地简化接收端译码的同时，通过空时编码提供一定分集增益。

在研究现有上行多用户空时检测算法的基础上，本文提出了一种新的多用户空时检测算法。算法利用空时编码的特性对接收信号进行重组，并将各用户投影到正交于其干扰空间的标准正交空间上实现用户间的干扰消除，各用户内部利用等效信道的正交性进行空时译码。进一步，给出了非理想信道环境下本文算法的设计过程，而仿真结果显示了本文算法的顽健性和有效性。

2 系统模型

假定一个上行多用户MIMO传输系统，K个终端用户各配置N个发射天线，基站配置M(MKN≥)个接收天线，假定接收端可以获得每个用户的信道状态信息（CSI），每个用户的信道服从准静态非频选莱斯衰落，则用户 k的信道矩阵kH 可以表示为

假定每个用户的数据发送前都进行正交空时分组编码(STBC)，编码时隙长度为T，记用户k的发送数据为则用户k发送的STBC码字矩阵可以表示为而 At, Bt( t = 1 ,… ,T )分别表示给定STBC实部和虚部系数矩阵，此时，基站在T个时隙内的接收信号矩阵Y为

其中，Z是加性高斯白噪声矩阵，其元素服从均值为0、方差为σ2的复高斯分布。

3 问题描述

根据第2节描述的信道模型，在接收端，基站通过一滤波器组{Gk,k=1,…,K}来实现各用户之间的分离：

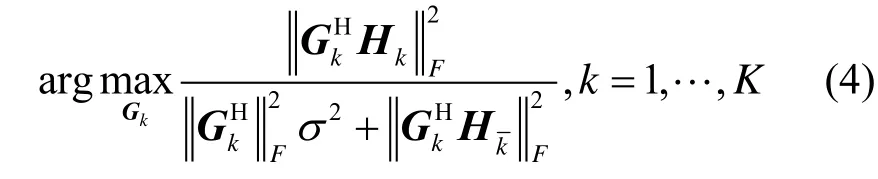
该优化问题是一个多变量优化问题，每个用户的最优滤波器设计将受所有用户信道矩阵的影响，这将导致求解每个用户的最优滤波器解析表达式变得十分困难。

鉴于以上分析，一种求解思路是基站首先通过组合迫零(CZF)或联合维纳(JWF)将多用户链路分离为K个平行的子信道，然后对于各个用户内部可以采用线性(linear)译码或者最大似然译码(ML)实现空时译码，这正是文献[9,10]提及的 CZF(JWF)+linear、CZF(JWF)+ML算法的核心思想。文献[11]提出一种分层联合空时处理的检测算法(LJSTD)，算法利用各用户发送码字的正交性这一性质进行空时译码，其突出特点是简单和易于实现，然而算法的缺陷在于滤波矩阵设计仍会导致期望用户接收信号内噪声的放大。文献[12]提出一种用户间串行干扰消除(U-SIC)的多用户检测算法，然而算法的固有缺陷误差传播会导致误码性能受限。

针对上述算法的缺点，本文提出的解决思路是利用各用户干扰空间的正交空间实现用户间的无扰分离，以用户k为例，滤波器kG设计如下：

4 本文算法求解上行多用户MIMO检测问题

4.1 用户采用相同空时编码方案

用户采用相同空时编码方案时，本文算法求解过程的关键步骤如下。

step1 接收信号线性重组。

记Y=[y1,…,yT],Z=[z1, …,zT]，根据STBC的性质，对式(6)作如下等效变换：

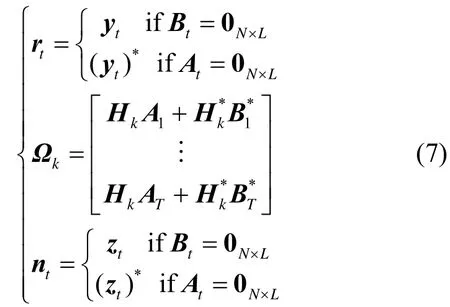
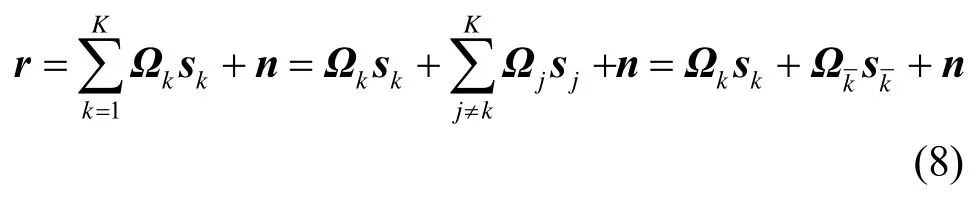
step2 用户间干扰消除。

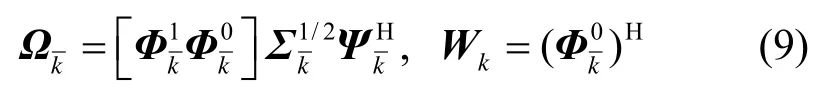
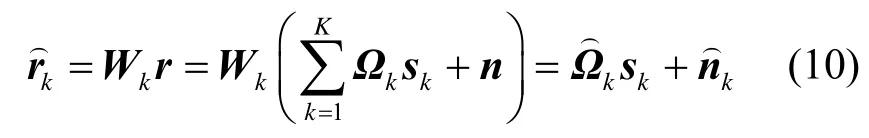
step3 用户内部STBC译码。

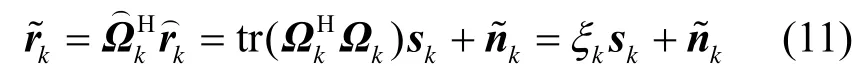
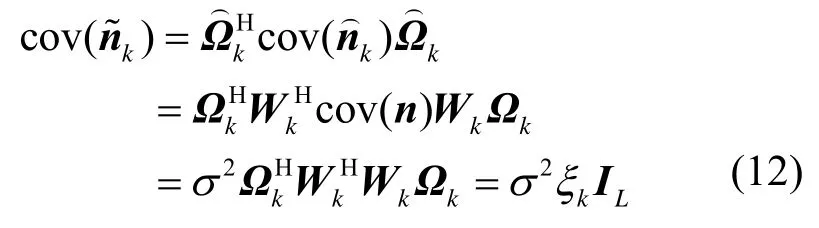
因此在给定信道ξkI条件下，用户k的容量可以表示为

4.2 用户采用不同空时编码方案

本节将讨论本文算法求解各用户采用不同的空时编码的状况。为了简化分析，考虑2用户，用户1采用3天线编码时隙为 T1= 8 复正交码字，用户2采用2天线编码时隙为 T2= 2的Alamouti编码，由于2用户采用的编码方案时隙不同，因此二者的公共时隙应为{T1, T2}的最小公倍数 T = 8 。不妨设2用户在 T= 8 内的发送码字矩阵分别为 X1和 X2，则而用户2发送码字矩阵每一个子块，其中，X( A)表示矩阵X中所有Aij≠0N×L组成的列向量，而X( B)表示矩阵X中所有Bij≠0N×L组成的列向量，此时，2用户联合发送码字矩阵可以设计为

在此假定条件下，基站在T个时隙内的接收信号矩阵为

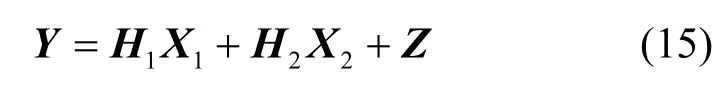
接收端，对于用户1而言，依次执行4.1节中的算法步骤，最终可得而对于用户 2，消除用户 1的干扰后，可得，也即

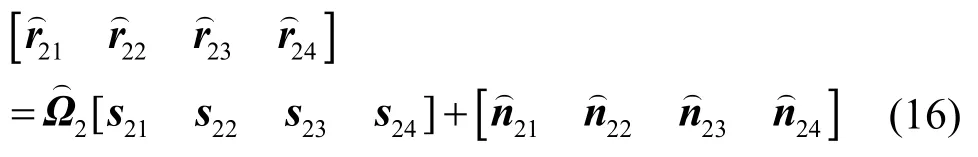
值得指出的是，当用户数目大于2且各用户采用其他的正交空时编码方案时，本文算法同样适用，其分析过程与上述2用户分析类似。

5 非理想信道环境下本文算法的设计

本节将重点分析存在信道估计误差的非理想信道环境下本文算法的设计过程。假定基站端所获得用户k的信道估计可以表示为

其中，Δk的元素和Hk的元素独立同分布，服从均值为0方差为的复高斯分布。在此假设下，重新考虑第3节中的多用户分离问题，也即寻找一匹配滤波器组{Gk,est,k =1,… ,K }，使得每个用户的估计接收信干噪比最大化：

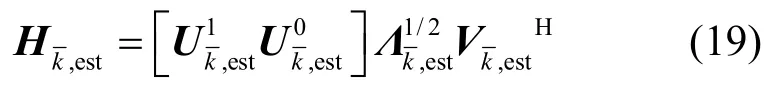
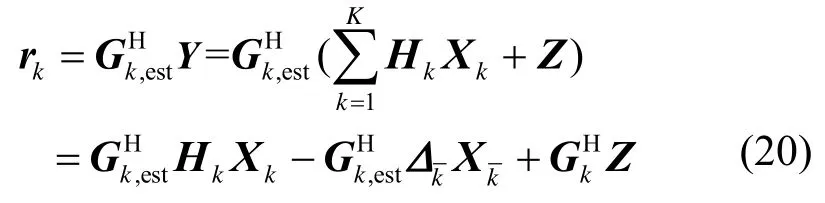
对于本文算法而言，与4.1节中一致，首先仍对接收信号进行空时线性重组，可得

为了消除用户k的多用户间干扰，对用户k干扰空间的信道估计进行SVD分解，以构造用户k匹配滤波矩阵Wk,est：

此时基站通过Wk,est所得用户k的接收信号可以表示为

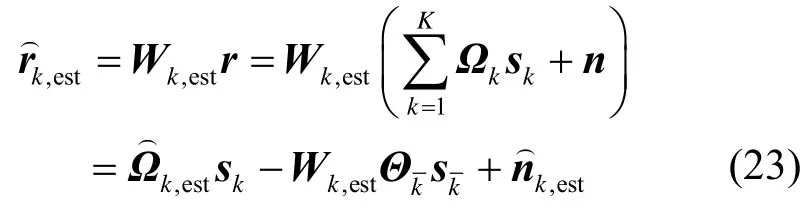
Wk,est由信道估计误差对用户 k带来的干扰。可以看出，由于信道估计不准确给用户k带来了干扰需要经过空时变换后用户k的等效信道矩阵能够提供一定的编码增益，以有效对抗其带来的影响。

6 仿真结果

考虑第 2节中描述的多用户上行链路传输模型，各用户的信道为准静态平坦非频选莱斯衰落。为了验证本文算法的有效性，仿真中同时引入CZF算法[9,10]、JWF 算法[9,10]、LJSTD 算法[11]以及 U-SIC算法[12]进行比较。仿真中上述算法采用相同上行链路配置：基站配置4天线，2用户各配置2天线发送Alamouti码字，采用QPSK调制。而对于用户采用不同空时编码的状况，本文算法的有效性通过与LJSTD算法进行比较，并从各用户的误比特率和等效信噪比2个角度来说明。为了方便起见，仍考虑2个用户的情形，用户1采用3天线1/2码率编码时隙为8复正交码字，用户2采用2天线码率为1编码时隙为2的Alamouti编码，基站配置5天线，调制方式采用QPSK。

实验 1 比较本文算法以及其他算法应用于上行多用户MIMO系统的误比特和容量性能。

图1给出上述几种算法的误比特性能随SNR变化曲线。本文算法的误比特性能要优于 LJSTD算法，在BER=10-3时，相对于LJSTD算法有3dB的增益。另外，本文算法在SNR较高的情况下误比特性能更好，这由图 1中的误比特率的斜率得出。U-SIC算法在信噪比较低时，其性能略优于LJSTD算法；而在信噪比较高时，则不如LJSTD算法。这主要是因为 LJSTD算法通过空时变换能够获得一定的分集增益，而U-SIC算法的误差传播固有缺陷导致其误比特性能受限，其性能和 JWF算法采用linear译码基本上一致，但要优于CZF算法。此外，无论对每个用户采用线性(linear)译码还是最大似然(ML)译码，采用联合维纳滤波(JWF)分离用户的误比特性能要优于采用组合迫零法(CZF)的误比特性能。进一步可以发现，在采用相同的滤波法(JWF或CZF)情况下，用户采用ML译码较linear译码能够获得一定的SNR增益。

图1 几种算法误比特性能随SNR变化曲线

图2给出了相应于图1中各种算法的10%中断容量随着SNR变化曲线。可以看出，本文算法相对于LJSTD算法能够获得3～4dB的容量增益。U-SIC算法获得较低的中断容量，其主要原因在于用户间干扰消除过程中干扰难以完全抑制，从而严重影响算法的容量性能。另外采用相同的滤波法(JWF或CZF)时，各用户采用linear译码时所获得的容量整体上高于各用户采用ML译码的状况。进一步，对于用户采用特定的译码方式(linear或ML)时，采用CZF滤波法所得容量要高于采用JWF算法所得容量。

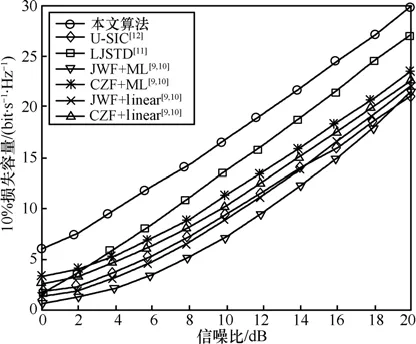
图2 几种算法10%中断容量随SNR变化曲线

实验2 分析本文算法在非理想LOS信道环境和NLOS信道环境下误比特性能的顽健性。

图3和图4分别给出了几种算法在视距（LOS）和非视距（NLOS）环境下存在6%信道估计误差时误比特率随SNR变化曲线。对比图3、图4和图1可以看出，当存在信道估计误差时，无论对于LOS还是NLOS信道环境，所有算法的误比特率性能变差，但U-SIC算法对于信道估计误差尤为敏感，因而其误比特率曲线急剧恶化，而本文算法受信道估计误差的影响最小，因而其顽健性在几种算法中最好。对于CZF算法和JWF算法而言，可以发现信道估计误差是影响其性能的主导因素，这直接导致2种算法下linear译码与ML译码性能基本上一致；另外对于6%信道估计误差，无论对于LOS信道环境还是NLOS信道环境，JWF算法在SNR＞14dB时误比特率曲线呈现地板效应。进一步观察图3和图4得知，对于同一种检测算法而言，LOS信道环境下的性能要明显优于NLOS信道环境下的性能，这是由于LOS环境相对于NLOS环境散射体更为丰富，从而能够提供更多的自由度。

图3 LOS环境6%信道估计误差时误比特率曲线

图4 NLOS环境6%信道估计误差时误比特率曲线

实验3 研究本文算法以及LJSTD算法应用于用户采用不同空时编码方案的上行系统。

图5给出了采用本文算法以及LJSTD算法，在2用户彼此采用不同的空时编码系统下的各个用户以及平均误比特率曲线。首先可以得出的结论是本文算法误比特性能优于LJSTD算法，这可以由图5中平均误比特率曲线或者单个用户的误比特曲线得出。进一步可以得出的结论是，整体系统的误比特性能取决于该系统中误比特性能最差的用户，用户1在采用本文算法和LJSTD算法下的误比特性能相差不到1dB，但是用户2采用本文算法时的误比特性能相比 LJSTD算法时的误比特性能获得近4～5dB的增益，这样本文算法平均误比特性能相比LJSTD算法时的性能可以获得4～5dB的增益。

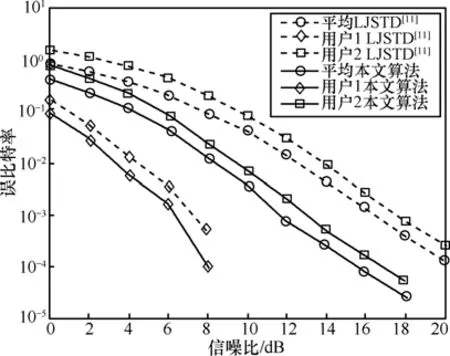
图5 本文算法和LJSTD算法误比特率比较曲线

为了进一步验证本文算法以及 LJSTD算法在用户采用不同空时编码系统下的性能，图6给出相应于图5中各用户的等效SNR比较曲线。各用户等效SNR直观上反应为图5中各用户误比特曲线的斜率，也可以理解为各用户所获得分集增益。图6从等效信噪比的角度给出了图5中2种算法误比特性能优劣的原因，各用户误比特性能越好则其所获得等效信噪比越高，本文算法性能优于LJSTD算法的原因在于，它能够使得每个用户所获等效信噪比得到进一步地提高，从而使整体系统误比特性能得到提升。

实验 4 本文算法以及其他算法复杂度的分析与比较。

为了进一步验证本文算法的有效性，对上述实验中的各种算法进行复杂度分析。而计算复杂度主要考虑检测过程中复数加法和乘法次数，以及求解滤波矩阵的计算量。由文献[13]可知，大小为q×q矩阵G的求逆运算( H-1)的计算复杂度等效为O( qw), 2＜ w＜3。大小为q×p矩阵H的SVD分解复杂度为 O (m ax(p q2, p2q , q3))，对于其Moore–Penrose伪逆 H†=(HHH )-1HH的计算复杂度等效为O( qw), 2＜w ＜ 3。表1给出几种算法的复杂度比较。其中，Ω为星座符号大小。

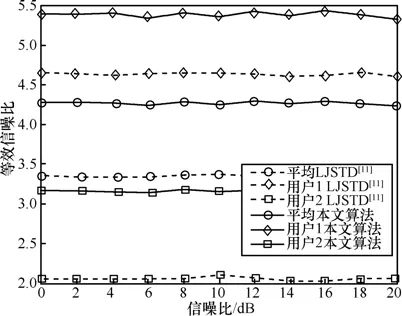
图6 本文算法和LJSTD算法各用户等效SNR比较

由表1可知，在不考虑计算滤波矩阵的情况下，各用户采用ML译码时具有最高的复杂度，是星座大小和天线数目的指数函数。而各用户采用 linear译码时复杂度最低；U-SIC算法无需计算滤波矩阵，因而其计算复杂度较低。LJSTD算法的计算复杂度和CZF(JWF)+linear算法差别不大，而本文算法复杂度高于LJSTD算法主要体现在计算滤波矩阵上，但要明显低于CZF(JWF)+ML算法复杂度。

7 结束语

本文提出一种新的上行多用户 MIMO系统检测算法，适用于各用户采用空时编码的情形。分析了本文算法在各用户分别采用相同和不同的空时编码系统下的求解过程，同时给出了非理想信道环境下本文算法的设计过程。仿真结果表明，同LJSTD算法相比，本文算法无论在各用户采用相同的空时编码方案还是不同的编码方案情况下，都具有更好的容量和误码性能。与U-SIC算法相比，本文算法在LOS信道环境和NLOS信道环境均具有更好的顽健性。而与 JWF(CZF)+ML算法和JWF(CZF)+linear算法相比，能够获得很好的误比特性能和计算复杂度之间的折中。

表1 本文算法和其他算法复杂度分析比较

[1] CHEN S, HANZO L. Minimum bit-error rate design for space-time equalization-based multiuser detection[J]. IEEE Trans on Communication, 2006, 54(5)∶ 824-831.

[2] FITZ M Y, MITRA M P. An improved bound on the performance of maximum-likelihood multiuser detection receivers in Rayleigh fading[J]. IEEE Transactions on Information Theory, 2006, 52(3)∶1184-1196.

[3] QIN Z L, CAI K, ZOU X X. Turbo multiuser detection based on local search algorithms[A]. IEEE Proceedings in the Internet Conf on Commun[C]. Singapore, 2007.5987-5992.

[4] ZARIKOFF B W, CAVERS J K, BAVARIAN S. An iterative groupwise multiuser detector for overloaded MIMO applications[J]. IEEE Transactions on Wireless Communications, 2007, 6(2)∶443-447.

[5] SUGIURA S Y, CHEN S, HANZO L. Reduced-complexity iterative markov chain MBER detection for MIMO systems[J]. IEEE Signal Processing Letters, 2008, 16(3)∶160-163.

[6] HENRIKSEN S, NINNESS B, WELLER S R. Convergence of markov-chain monte–carlo approaches to multiuser and MIMO detection[J].IEEE Journal of Selected Area in Communications, 2008,26(3)∶497-505.

[7] MA W K, CHING P C, DING Z. Semidefinite relaxation based multiuser detection for M-ary PSK multiuser systems[J]. IEEE Trans on Signal Processing, 2006, 52(10)∶2862-2872.

[8] MAO Z W, WANG X M, WANG X F. Semidefinite programming relaxation approach for multiuser detection of QAM signals[J]. IEEE Trans on Wireless Communications, 2007, 6(12)∶4275-4279.

[9] KAZEMITABAR J, JAFARKHANI H. Multiuser interference cancellation and detection for users with more than two transmit antennas[J].IEEE Trans on Communications, 2008, 56(4)∶574-583.

[10] NAGAO Y, KUROSAKI M, OCHI H. Low-complexity group layered space-time detection in spatial correlated MIMO channels[A].IEEE 65th Vehicular Technology Conference[C]. Ireland, 2007.233-2237.

[11] DAI L, SFAR S, LETAIEF K B. A quasi-orthogonal group space-time architecture to achieve a better diversity-multiplexing tradeoff[J].IEEE Trans on Wireless Communication, 2007, 6(4) ∶1295-1307.

[12] MICHAEL L H. Advances in Multiuser Detection[M]. USA∶Wiley-IEEE Press, 2009.

[13] GOLUB G H, VAN L C F. Matrix Computations[M]. Baltimore, MD∶the John Hopkins Univ Press, 1996.