一种自适应TIN 迭代加密滤波算法
2010-08-06薛晓滨卢建康
殷 飞 齐 华,2 薛晓滨 卢建康
(1.西南交通大学信息科学与技术学院,四川成都 610031;2.西南交通大学土木工程学院,四川成都 610031;
3.中铁二院工程集团有限责任公司信息中心,四川成都 610031;
4.中铁二院工程集团有限责任公司测绘分院,四川成都 610031)
机载激光雷达测量(Light Detection and Ranging)技术是近些年快速发展起来的一种空间信息获取技术,能够快速高效地获取数字地表三维模型。目前,LiDAR系统硬件技术发展得比较成熟,大部分属于硬件及系统集成方面的问题已得到解决。但数据后处理技术却发展相对滞后[1],主要包括滤波分类、地物提取、三维重建及海量点云数据简化。“十一五”期间,国家863计划地球观测与导航技术领域也开始进行LiDAR数据后处理方面的研究[7]。
机载激光雷达系统采集到的原始数据点离散分布于三维空间,这些点可能打到真实地表面,也有可能打到植被或人工建筑物等地物表面。为了从点云数据中得到数字高程模型,需要分离地面点和地物点,即Li-DAR数据滤波。作为LiDAR数据后处理最为重要的组成部分之一,滤波结果直接影响所生成DEM(Digital Elevation Model)的质量,也是进行地物提取与三维重建的必要前提。
如何实现由LiDAR数据快速、准确地提取出地面点,一直是国内外专家学者们研究的重点、难点和热点之一。出于商业方面的考虑,现有的几种商业软件其数据处理算法都不对用户公开。
1 滤波原理及方法回顾
LiDAR数据滤波的原理基于高程突变,即邻近的两个激光点间高程变化较大时,一般认为不是由于地形的陡然起伏所造成的,更为可能是由于地面存在地物而引起,高程较大的点很可能是地物点。若两点间的距离越近,高差越大,较高的点更有可能为地物点。故判断某点是否地面点时,要考虑该点到参考地面点的距离。随着两点间距离的增加,其高差也会变大[6]。
迄今为止,国内外的专家学者对滤波算法进行了深入研究。最简单的滤波算法认为一定区域内高程最低的点即为地面点;该算法基于平坦地形,误差较大。德国斯图加特大学的Lindenberger提出了数学形态学滤波算法,对LiDAR数据进行形态开运算并利用自回归过程改善开运算的结果[4]。奥地利维也纳大学的Kraus和Pfeifer提出了迭代线性最小二乘内插滤波算法,根据计算得到的残差值给每一个激光点赋权值,由此分离出地面点[3]。Vosselman提出了基于坡度的滤波算法,根据最大坡度 γ和垂直测量精度 σz确定高差阈值函数[6]。Axelsson提出了三角网迭代加密滤波算法,通过不断向三角面加入满足高差阈值和角度阈值的激光点,达到重建地表面的目的[2]。武汉大学张小红提出了移动曲面拟合滤波算法,用二次曲面去拟合空间曲面,拟合值与原始值间高差小于阈值则视为地面点[8]。
目前还没有哪一种滤波算法对任意地形的处理结果都很完美。Sithole通过实验分析了8种典型滤波算法,指出各种算法都存在一定的问题[5]。本文通过研究三角网迭代加密滤波算法,提出了一种改进方法。
2 滤波算法
数据处理过程中,若将原始离散激光点云内插为规则格网DSM(Digital Surface Model)格式,虽然可以引入成熟的图像处理算法,但势必会引入误差,另外数据的精度也会降低。在原始LiDAR数据中,相同的平面坐标可以对应多个不同高程值的激光点。以规则格网DSM表示时,一对X、Y坐标只能对应一个高程值。因此,认为规则格网表示方式会在一定程度上丢失数据原有的某些属性,本文选择对基于离散点的三角网迭代加密法进行改进。
Axelsson提出的三角网迭代加密滤波算法思想:首先对测区进行分块处理(分块大小以测区地物最大长度为准),初始点选择地面上一些高程较低的点,然后选取每块中的最低点作为初始地面点并建立不规则三角网模型。定位待判断点P对应的三角形,P及其在三角面上的投影点与三角形顶点间的角度分别记为α、β、γ,P到三角面的垂直距离记为d。若 α、β、γ和 d都小于设定的阈值,则接受该点为地面点并重新建立三角网(见图1)。接着判断下一个点,直到所有的点都被分为地面点或非地面点。通过不断地加入满足条件的激光点来扩大地面模型,每加入一个新点都更新不规则三角网,最终得到非常接近地表面的三角网模型[2]。

图1 滤波算法参数示意
经研究,该算法存在的主要缺点有:
①该算法假定一定区域内高程最低的点为地面点,此时如果存在低于地面的点,则会错误分类到地面点类,因此需要先分离低点。此外,没有考虑空中噪点对滤波算法的影响。
②参数值不能随着地形自适应改变。在绝对理想的平地区域,各激光点的高差为0,若此时的高差阈值还取一固定值,不可避免错误地将地物点分类为地面点。此外,陡坡边缘的点可能被错误分类为地物点。
针对上述问题,本文对该算法作了以下改进,算法流程见图2。
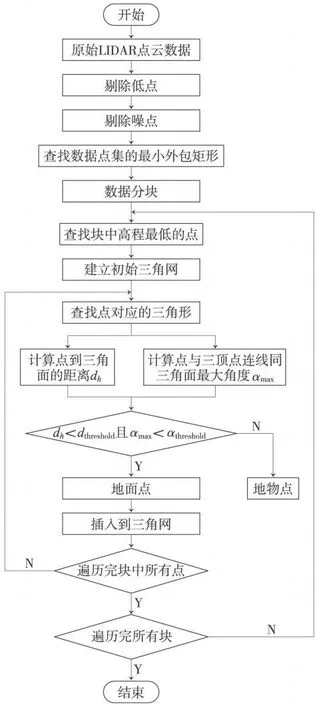
图2 算法流程
(1)对原始激光点云数据进行预处理,剔除错误点,包括低点、噪点等。
剔除单个低点:
若某一个点为低点,则其高程值与领域内其他点的高差都应满足一定的高差阈值。设待判断点为Pa,以Pa为中心点,搜索一定邻域范围内的其他激光点,若对邻域内任意激光点P都有ZPa-ZP<-H,H为设置的高差阈值,则可判断Pa为低点。用数学形式表达为:对于激光点云集P,若其邻域内任一点满足:PT={Pa∈P|∀Pr∈Pn:ZPa-ZP<-H},则判断 Pa为低点 。
剔除低点簇:
若某点的邻域内几个连续点均为低点,则其高程与内插高程之差应满足一定的高差阈值。设低点簇中的某个待判断点为Pa,以Pa为中心点,搜索一定邻域范围内的其他激光点并进行插值,其内插高程为Pi,若ZPa-ZPi<-H,H为设置的高差阈值,则可判断Pa为低点(见图2)。该方法也可用于剔除单个低点。
本文提到的噪点专指空中点,噪点不仅会影响数据浏览,还会影响滤波算法的使用,所以应先剔除这些点。由于这些点的高程与周围点高程相比突变较大,一般可以通过设置绝对高程阈值去除。
(2)对测区分块并建立虚拟格网索引,取每一块中高程最低的点PL作为种子点。查找块的凸包并将PL的高程赋给边界点,由凸包与PL建立初始三角网,此时所有三角形位于同一平面。根据测区情况设置初始高差阈值。
(3)分块时保证各块间有一定程度的重叠。
(4)高差阈值设置为自适应函数。
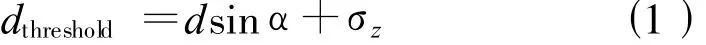
式中 α——待判断点对应三角形的坡度;
d——激光点的平均间距;
σz——输入的常数。
3 滤波实验及分析
3.1 滤波实验
为了有针对性地比较滤波算法,特地选择了两块典型区域的数据进行滤波实验。
实验数据1为某城区实测LiDAR数据,数据区域为长方形,测区面积为250 m ×250 m,原始文件5.68 M,点数为213093个,平均间距约0.77 m,密度约3.4个/m2。原始数据中包含有低点,该区域地形平坦,建筑物较多且复杂,地物主要为植被、汽车、房屋、桥梁等,见图 3(a)。
实验数据2为某森林区域实测LiDAR数据,测区面积为146 m ×80 m,原始文件1.57M,点数为58 894个,平均间距约0.46 m,密度约5个/m2。该区域地形平坦,地物主要为植被,见图3(b)。
由图4(a)、图4(b)可看出,改进后算法剔除了错误点、小汽车等近地点。同时有少数面积较小的房屋未过滤,形成小的突起,房屋边缘的过滤效果不是很理想。此外有部分道路点被错误分类为地物。

图3 实验数据

图4 城区滤波结果晕渲图

图5 森林区域滤波结果晕渲图
由图5(a)、图5(b)可看出,森林区域采用改进后算法处理的结果过滤了大部分植被,但仍有少数极低的灌木点错误分类为地面点,同时将部分地面点错误分类了地物点。
3.2 滤波难点分析
机载激光雷达数据滤波结果与激光点的密度、测区地形和地物的复杂程度都有很大关系。一般情况下,大多数滤波算法都能够处理地形、地物不复杂的区域,如平原、城市、稀疏的树林等。从工程实践可知:困难区域的处理是一个难点。因此,能否准确对任意复杂地形、地物进行滤波处理是评价滤波算法优劣的一个重要指标。为了定性分析滤波算法,特选取几处滤波难点,包括错误点、复杂地物、附着地物、植被(低矮植被和坡面上的植被)等(如表1)。
3.3 定量分析
ISPRS组织第Ⅲ委员会第三工作组于2004年发布了滤波方法比较报告,文章中将滤波误差分为两类。第Ⅰ类误差:将地面点错误分类为地物点;第Ⅱ类误差:错误接收地物点并归入地面点[5]。

表1 滤波实验定性比较
第Ⅰ类误差:

第Ⅱ类误差:

总误差:

式中 a——正确标识为地面点的数目;
b——错误分类为地物点的数目(由于第Ⅰ类误差产生);
c——错误分类为地面点的数目(由于第Ⅱ类错误产生);
d——正确分类为地面点的数目。滤波算法考虑最小化第Ⅱ类误差,即应剔除尽量多的地物点,当地物很小或很贴近地表面时,甚至可以剔除部分真实地面点。其原因是第Ⅱ类误差对DEM质量的影响比第Ⅰ类误差要大(如表2、表3所示)。

表2 数据1滤波结果定量比较
三角网迭代加密算法将部分低矮植被点和近地点错误分类为地面点,导致第Ⅱ类误差较大。改进后采用坡度阈值函数,有效剔除了低植被点,处理结果的第Ⅱ类误差减小,总误差有一定程度减小。同时由于剔除了部分真实地面点,导致第Ⅰ类误差变大。

表3 数据2滤波结果定量比较
4 结论
通过研究三角网迭代加密滤波算法,提出了一种改进方法。在滤波处理前先剔除错误点,以降低其对后续算法的影响。针对不同地形情况的参数设置是一个难点,提出了根据三角形坡度建立自适应阈值函数的方法,并选择两块典型区域数据验证了改进后滤波算法的可行性。实验证明:该方法能够有效处理Li-DAR数据,剔除错误点和近地点并得到DEM数据,且第Ⅱ类误差、总误差相对减小。但是过滤小面积房屋的效果不是很好,可以考虑结合回波信息进行处理。此外,由于LiDAR数据是海量数据,本算法中又涉及动态构建不规则三角网,其时间复杂度较高。因此,选择速度较快的构网方法是降低滤波时间复杂度的关键。
[1]Axelsson P.Processing of laser scanner data-algorithmsand applications.ISPRSJournal of Photogrammetry and Remote Sensing,1999,54:138-147
[2]Axelsson.DEM generation from laser scanner data using adaptive TIN models.International Archives of Photogrammetry and Remote Sensing,2000,33(B4):110-117
[3]Kraus K,Pfeifer N.Determination of terrain modelsin wooded areas with airborne laser scanner data.ISPRS Journal of Photogrammetry and Remote Sensing,1998,53:193-203
[4]Lindenberger J.Laser-profilmessungen zur topographischen gelandeaufnahme. Verlag der Bayerischen Akademie der Wissenschaften,1993
[5]Sithole G,Vosselman,G.Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds.ISPRS Journal of Photogrammetry and Remote Sensing,2004,59:85-101
[6]Vosselman G.Slope based filtering of laser altimetry data.IAPRS,2000,33(B3/2):935-942
[7]科技部.863计划地球观测与导航技术领域2006年度专题申请指南[R].北京:科技部,2006
[8]张小红.机载激光雷达测量技术理论与方法[M].武汉:武汉大学出版社,2007
