地方独立坐标系与WGS-84坐标系转换方法及应用
2010-08-06蒋小军宋占峰吴清华
蒋小军 宋占峰 吴清华
(中南大学土木建筑学院,湖南长沙 410004)
1 概述
城市道路是城市社会活动、经济活动的纽带和动脉,是城市综合功能的重要组成部分,也是城市建设水平的集中体现。最近几年,我国的城市化发展突飞猛进,城市基础设施建设力度加大,城市道路的建设迎来了黄金时期,给城市道路的设计工作者既带来了机遇,也提出了更新、更高的要求。传统的城市道路设计理念或设计流程存在几个方面的局限性:①线路设计在二维的地形图上进行,地形地物的判别不直观;②地形图的范围有限,设计人员的视野较窄,难以综观全局;③二维地形图提供的信息有限,难以叠加区域三维建筑物、地质等重要信息。
近年来,随着数字摄影测量技术、GIS技术、虚拟现实等高新技术发展,数字地球技术取得重要突破,以GoogleEarth为代表的数字地球软件先后推出,为上述问题的解决提供了较好的途径。GoogleEarth是拥有全球范围丰富卫星影像和地形数据的三维数字地球平台。这些卫星影像分辨率较高,现势性较好,对道路规划、方案评审、环境评估具有重要意义。
在城市道路工程的设计中,所使用的地形资料大多是在地方独立坐标系下获得的。为了将外业实测数据在GoogleEarth上进行三维表示,就必须实现地方独立坐标与WGS-84之间的转换,而地方独立坐标系大都基于北京54坐标系建立的,所以一般以北京54坐标系为过渡坐标系,即地方独立坐标系⇔北京54坐标系⇔WGS-84坐标系,三类坐标的椭球参数都不尽相同,必须使用相应的数学模型进行转换。
2 椭球参数简介
(1)WGS-84的椭球参数
椭球长半径a=(6378137±2)m;
地球(含大气层)引力常数 GM=(3 986 005×108±0.6 ×108)m3/s2;
正常二阶带谐系数 C2.0=-484.166 85×10±0.6 ×10-6;
地球自转角速度 ω=(7292115×10-11±0.15×10-11)rad/s;
利用以上四个参数可以求出WGS-84椭球扁率f=1/298.257 223 563。
(2)北京54参考椭球(克拉索夫斯基椭球)
椭球长半径a=6 378 245 m;
椭球扁率f=1/298.3;
地方参考椭球一般选择与当地平均高程相对应的参考椭球,该椭球的中心、轴向和扁率与北京54参考椭球相同,其椭球长半径则有一改正量 Δa,如图1所示。
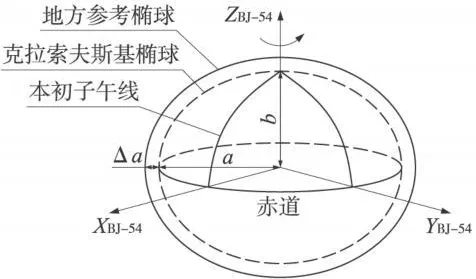
图1 地方参考椭球与北京54参考椭球的区别
3 坐标转换步骤及模型
坐标转换流程如图2所示。
3.1 同一参考系下的平面坐标转换模型
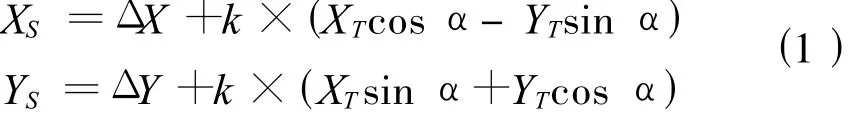
式中 ΔX、ΔY——x和y方向上平移系数;k、α——比例系数和旋转角度。
3.2 布尔莎(Bursa)模型
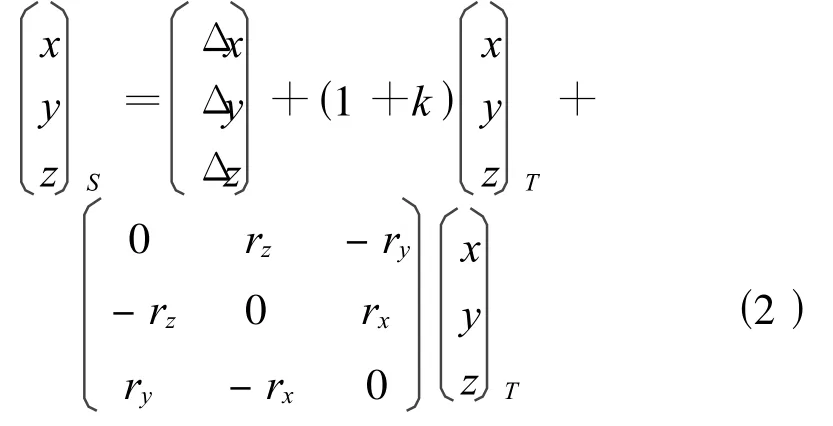
式中,Δx,Δy,Δz,k,rx,ry,rz为七参数。
考虑坐标数据的有效位数(32位操作系统上,C++语言的最高示数精度一般为15~16位),布尔莎模型在使用最小二乘法计算七参数的过程中将损失精度,故不能使用该模型直接计算七参数,但可用于确定七参数之后的回代计算。
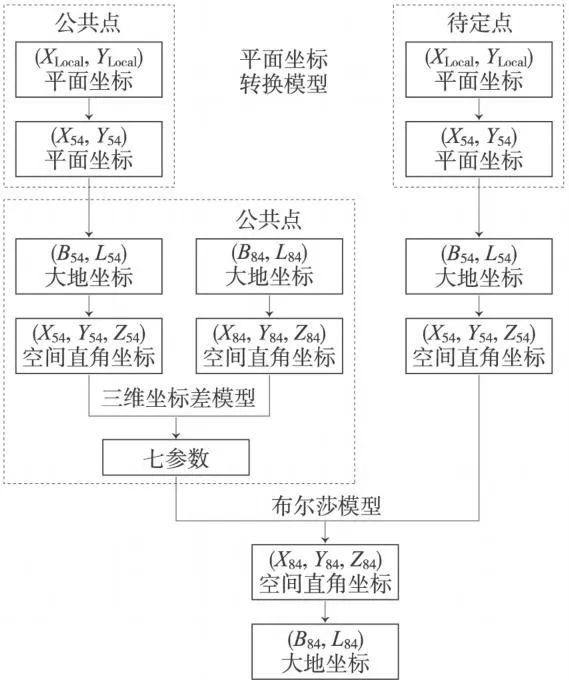
图2 地方独立坐标系与WGS-84坐标系转换流程示意
3.3 三维坐标差转换模型
该模型是由布尔莎模型推导而来,假设有n(n≥3)个公共点,那么第 i(0 <i≤n,i≠j)个公共点坐标为(xi,yi,zi),第j(0 <j≤n,j≠i)个公共点坐标为(xj,yj,zj),设 Δxij=xj-xi,Δyij=yj-yi,Δzij=zj-zi,则三维坐标差转换模型
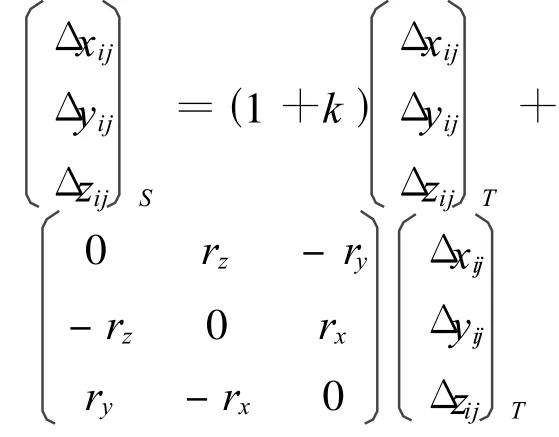
或
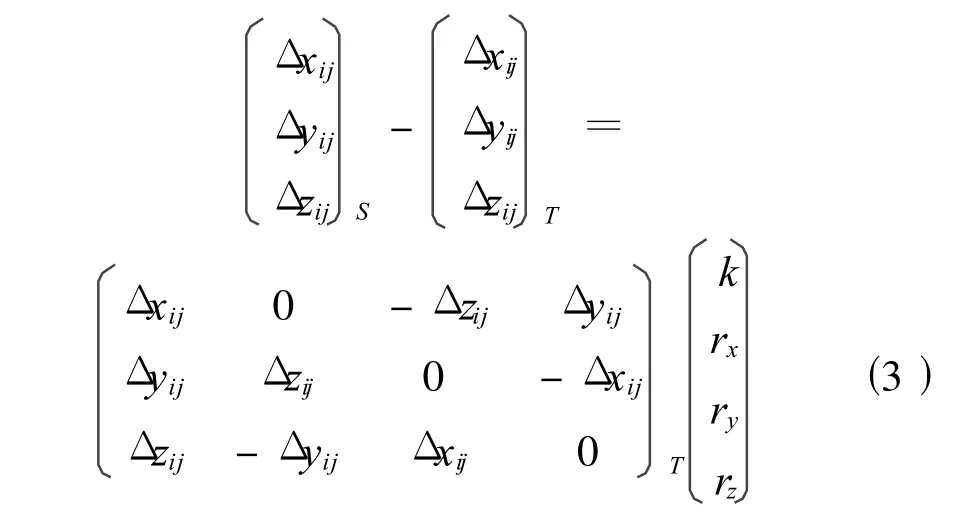
写成矩阵形式为

故求解该七参数可归结为线性代数方程组的求解,对于这样一类问题有多种求解方法,用的最多的是Gauss-Jordan消去法、正规方程组等。
在计算过程中,至少有两个附加的因素会导致数值计算上的错误:
①虽然有些方程并非彼此精确的线性组合,但它们可能很接近线性相关,而在求解过程的某个阶段,机器的舍入误差使它们成为线性相关,这时计算程序将失败。
②求解过程中,舍入误差的积累也会使结果与真实解之间相差甚远。这个问题在矩阵维数很大时特别容易发生,但计算进程在算法上并无错误。然而将结果直接回代到原来的方程就会发现,由它计算出来的x解集却是错误的。由于求解过程中会不断发生相近抵消,方程组越接近奇异,这种情况越易发生。事实上所计算的项可视为有效数字被全部舍去的特殊情况。
针对以上两种数值计算错误,Gauss-Jordan消去法、正规方程组都是不稳定的。为了获得高精度的七参数值,最好采用奇异值分解法。相比其他算法,奇异值分解的不足在于需要用额外的内存来存储设计矩阵,且运算速度明显要慢。但它最大的优点是:在理论上,它始终会得出有效的解集。
4 实例分析
以长沙市雨花路为例。长沙独立坐标系的建立仍采用克拉索夫斯基椭球,中央子午线定在城市中央,为112°50′00.0000 ″E 。公共点坐标见表 1 。

表1 公共点坐标
4.1 四参数计算
长沙平面坐标转北京54的四参数值为
x向平移:Δx=3 021 287.8529 m
y向平移:Δy=465 391.082 3 m
比例系数 :k=1.0 ×10-6
旋转角度:α=-1975.224 3″
上述参数值由GPS测量提供,也可使用最小二乘法拟合公共点得出。
4.2 七参数计算
由于北京54坐标系下的大地高往往不能精确得出,同时实验证明高程误差对平面坐标转换精度影响较小,故使用长沙独立坐标系正常高代替北京54的大地高来解算七参数,从而得出七参数值(如表2所示)。

表2 转换七参数
4.3 实验结果
该算例中,AutoCAD图形文件中房屋建筑所在坐标系统为长沙独立坐标系,使用Google Earth二次开发技术,将长沙市雨花路数字地形图转换到Google Earth上,通过与Google Earth原有影像地形图进行对比,所绘制的三维房屋建筑位置能够很好的吻合已有的地形数据(如图3所示)。
使用上述七参数进行转换,在Google Earth中绘制三维建筑与线路(如图4)。
5 结论
通过对地方独立坐标系与WGS-84坐标转换算法的介绍以及实例分析,可得出以下结论:
①地方坐标系下的高程异常一般无法准确获得,同时高程误差主要表现为对高程转换精度的影响,而对平面坐标转换精度影响较小。所以在解算七参数时,通常使用地方正常高代替北京54坐标系下的大地高,进行最小二乘拟合。
②从参数求解过程中及已知点回代误差统计中可以发现,在已知点中存在个别粗差点,会扭曲与降低转换参数的确定精度,所以最好将粗差点剔除后重新计算,以获得更高精度的转换参数。
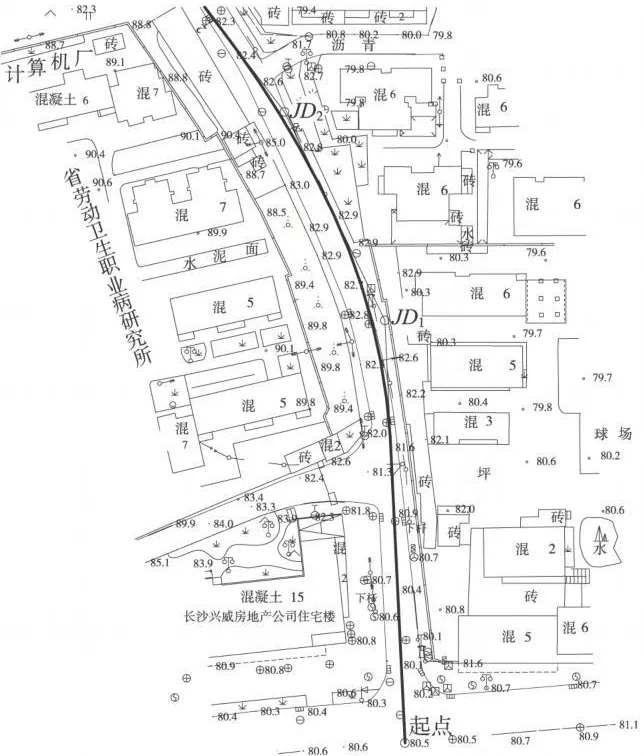
图3 长沙市雨花路AutoCAD数字地形
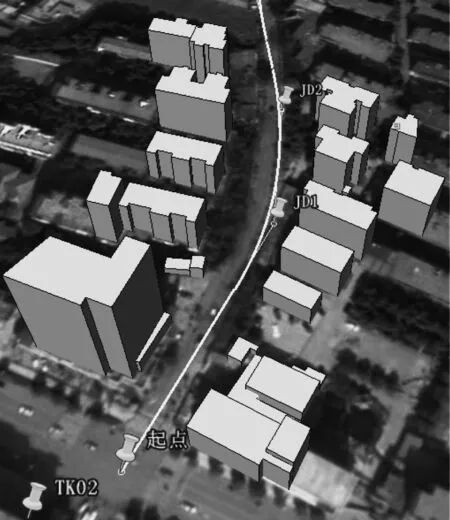
图4 长沙市雨花路Google Earth三维地形
[1]赵长胜.高斯投影坐标反算的迭代算法[J].测绘通报,2004(3):16-17
[2]张晓帆,周可法,赵同阳,等.关于利用七参数法进行WGS-84和BJ-54坐标转换问题的探讨[J].测绘与空间地理信息,2007,30(5):33-42
[3]王解先,邱杨媛.高程误差对七参数转换的影响[J].大地测量与地球动力学,2007,27(3):25-38
[4]吴吉贤,杨志强,张耀文,等.BURSA模型应用于 BJ54与WGS84坐标转换的讨论[J].高原地震,2006,18(3):32-35
[5]张 勤,李家权.GPS测量原理及应用[M].北京:科学出版社,2005
[6]李征航,黄劲松.GPS测量与数据处理 [M].武汉:武汉大学出版社,2005
[7]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2001
[8](美国)普雷斯,等著.胡健伟,等译.C++数值算法[M].北京:电子工业出版社,2005
