斜轴墨卡托投影模型及其应用分析

2010-08-06陆鹏程林冬伟

铁道勘察 2010年4期

陆鹏程林冬伟

(1.同济大学测量与国土信息工程系,上海 200092；2.中船勘察设计研究院有限公司,上海 200063)

1 概述

我国高速铁路建设正在大规模开展,对测量的精度要求很高。根据《客运专线无砟轨道铁路工程测量技术暂行规定》要求,平面坐标系统采用工程独立坐标系,坐标系的设计满足如下要求[1]：边长投影在对应的线路设计平均高程面上(轨面高程)；投影长度的变形值不大于10 mm/km。按照这种要求,当前工程中常用的高斯投影在不考虑高程对长度变形影响的情况下,东西方向最多只能控制50多km,这样就会导致一条东西跨度较大的铁路沿线需要建立多个独立坐标系,给整条铁路工程施工带来很多不便。本文提出沿铁路线方向,采用等角斜切圆柱投影即斜轴墨卡托投影的原理、方法、计算步骤,使圆柱面与线路中心线相切,并通过数据分析其应用于高速铁路测量的优越性。

2 斜轴墨卡托投影的基本原理、方法、计算步骤

墨卡托投影是一种保角圆柱投影[2]。它以圆柱作为投影面,将经纬线投影到圆柱面上,将圆柱面展成平面而成。圆柱面可与地球椭球相切或相割,根据位置的不同,分为正圆柱、横圆柱、斜圆柱三种。圆柱投影示意图如图1所示,其中图1(a)为正圆柱,图1(b)为横圆柱,图1(c)为斜圆柱。

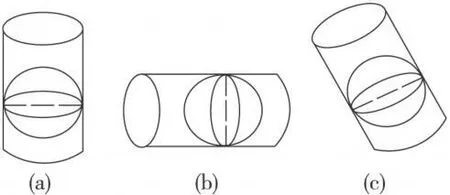
图1 圆柱投影示意

正轴圆柱投影适用于低纬度地区或沿纬度线扩展的区域,假如投影区域是沿除赤道圈以外的某一大圆方向,或沿经线方向伸展的地区,则可考虑采用斜轴或横轴圆柱投影以改善投影条件,从而使变形减小。

采用斜轴圆柱投影时,用椭球体表示地球则计算甚为不便,在几百公里的工程范围内,通常将地球椭球体视为半径等于R的圆球体,斜轴投影与半径R的圆球体相切的大圆称投影中线,投影前后其长度保持不变。离开投影中线的点会产生长度变形,其变形性质与高斯投影类似。若线路工程东西长度太长(超千公里),圆球表示地球带来的误差将不可忽视,宜分段处理。

2.1 选择投影参考圆球

设线路工程范围中心某点经纬度为(B0,L0),线路设计平均高程面(轨面高程)为H0,假设基准点为(B0,L0,H0),在基准点处投影圆球的半径方向与WGS-84椭球法线重合,投影圆球球面通过基准点(B0,L0,H0),使线路设计平均高程面位于投影参考圆球上。

投影圆球的半径(即中心线走向的法截弧半径)取为

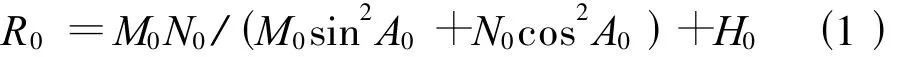
式中：A0为线路工程中心线走向的大地方位角,M0、N0分别为工程中心基准点处的子午圈和卯酉圈半径。

2.2 建立圆球空间直角坐标系

设X′轴为过球心指向基准点P(B0,L0,H0),过基准点P沿椭球大地方位角A0方向形成的投影圆球的大圆为投影圆球的假想赤道面,过基准点P垂直于假想赤道面的大圆为假想零子午面,Z′轴为过球心垂直于假想赤道面(如图2所示)。

图2 椭球空间直角坐标系与圆球空间直角坐标系

设基准点(B0,L0,H0)所对应的WGS-84空间直角坐标为(X0,Y0,Z0),计算公式为

则各控制点在新投影圆球空间直角坐标系中的坐标计算公式为

则基准点坐标(B0,L0,H0)在圆球空间直角坐标系中的坐标为(R0,0,0)。

2.3 投影圆球球面坐标经纬度

显然各点并非正好都位于投影圆球的球面上,而参考圆球体表面与地面越吻合则投影变形越小。一般来说,对于地势起伏不大的线路工程,选择合适的投影圆球半径,使得圆球表面与测区表面大致吻合,就能比较好的控制高差投影差影响；对于地势起伏较大、范围较广的线路工程,要控制高差投影差的变形,可以采取将各点沿其重力线方向投影到投影参考圆球球面上,而非用投影圆球的半径方向代替。在垂线偏差较小的情况下,可将椭球的法线看作是该点的重力线方向。

各点距投影圆球球面的高度为

各点法线在椭球空间直角坐标系中的矢量为(cos B cos L,cos B sin L,sin B)T。

考虑高度H′引起的改正后,圆球球面上点的空间直角坐标为

根据球面各点的坐标(X″,Y″,Z″),则可计算斜轴圆球上的经纬度为

2.4 斜切圆柱投影坐标

斜轴墨卡托投影中,要使线路中心线的长度在投影前后保持不变,就要将圆柱面沿线路工程中心相切,即取圆柱面沿投影参考圆球的假想赤道线相切。圆柱面展开后,设投影后的假想赤道线为x轴,假想零子午线为y轴,则圆球面上假想的纬度圈展开后就是x轴的平行直线,假想子午圈成了y轴的平行直线。

切圆柱投影的一般公式为

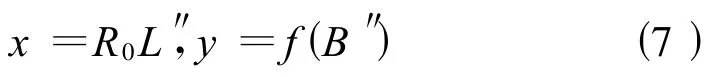
即保持线路中心线(x轴)的长度不变。

投影变换条件主要包括等距离变换、等角度变换和等面积变换。为了在常规测量中的边角改化方便,本文采用等角度投影

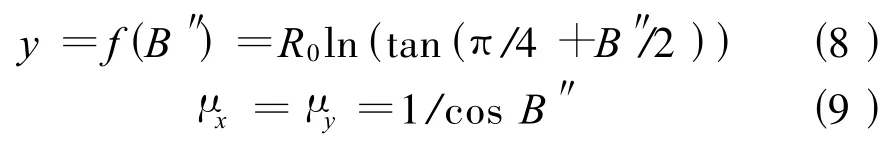
采用等角度投影,可以保持投影前后各点的方向值不变；离线路中心线越远,则长度变形越大,但各方向上的长度变形相等；等角度投影便于常规测量中的边角改化换算,即角度不变,边长乘以相应变形系数。

3 斜轴墨卡托投影的应用

在工程测量实际应用中,距离投影长度综合变形主要由高差投影变形和高斯地图投影变形两部分组成[3-4]：

①将实际测量真实长度归化至国家统一的椭球面上,会产生高差投影变形。

②将椭球面上的长度投影到高斯平面上,会产生地图投影变形。

由高速铁路工程实际情况可知,要使高差投影变形小于1/10万,则线路的高程至归化高程面的距离不宜大于60 m；要使高斯投影变形值不大于1/10万,应将投影带边缘至中央子午线的距离控制在28 km以内,即投影带东西向的宽度不大于56 km。

而工程实际情况是,对于一些东西走向范围较大的线路工程来说,采用上述做法就需要根据线路分布范围选取不同中央子午线划分区域,导致高斯投影带的宽度较小,投影带数量过多,施工过程中将频繁进行投影换带计算,严重影响施工变形精度的控制。

因此,采用斜轴墨卡托投影,目前一般方法是建立斜轴投影坐标系,即将地球假设为一个圆球体,通过在圆球上建立极坐标系过渡来计算斜轴圆球上各点的经纬度[5,6],进而再投影到平面上。将线路走向的中心线作为投影中心线,在切圆柱投影时将圆柱面与线路的中心线相切,使线路范围内点到投影中心线的距离小于28 km,满足2.2中地图投影的要求；同时通过参考圆球的半径选择,使圆球球面与测区表面大致吻合,控制高差投影变形的影响。

本文介绍的斜轴墨卡托投影,同样是将地球假设为一个圆球体,所不同的是建立投影圆球空间直角坐标系来过渡计算圆球上的经纬度,再采用切圆柱投影来满足地图投影的要求；对于高差投影变形的影响,采取将各点沿其重力线方向投影到投影参考圆球球面上,而非用投影圆球的半径方向代替。在垂线偏差较小的情况下,可将椭球的法线看作是该点的重力线方向,这对于高差投影差的控制具有重要意义。

图3是某线路工程各点在WGS-84椭球面上的经纬度分布图,可知线路走向大致是东西方向,且东西范围跨度较大。采用斜轴墨卡托模型计算,选取测区中央4号点为基准点,建立线路工程独立坐标系(点4为原点)。表1为各点在WGS-84椭球上的经纬度,其空间直角坐标由转化而来。

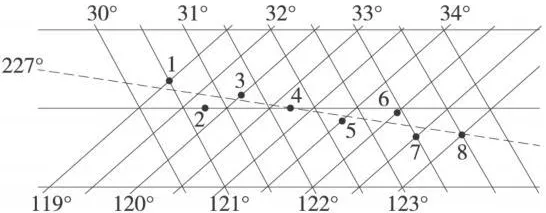
图3 线路上各点经纬度分布

表1 某线路工程各点WGS-84椭球经纬度及空间坐标

确定线路设计平均高程面(轨面高程)为165.5 m,线路中心线走向大地方位角分别取两个不同值,可得到下面两个算例结果。

3.1 算例一

设线路工程区域中心线走向的大地方位角为224°00′00″,则投影参考圆球的半径R0=6 368 171.619 082 55 m。表2为各点在投影圆球球面上的经纬度和投影后的平面坐标以及长度变形。

3.2 算例二

设线路工程区域中心线走向的大地方位角为227°00′00″,则投影参考圆球的半径R0=6 369 791.471 096 39 m。表3为各点在投影圆球球面上的经纬度和投影后的平面坐标以及长度变形。

表2 斜轴墨卡托投影结果(一)

表3 斜轴墨卡托投影结果(二)

从本文所述斜轴墨卡托投影原理,计算过程和表1、表2的计算数据可以看出：

(1)斜轴墨卡托投影是将地面点投影到平面的投影,从地球椭球面到投影圆球球面和从球面到斜轴墨卡托投影都是等角投影,即在整个投影过程中角度不变形,符合一般工程测量和高速铁路工程测量的要求和习惯。

(2)由表1和表2的数据可以看出,算例二的线路走向大地方位角取得更为合理,长度变形更小。算例一的投影长度变形最大为0.732 8/100 000,算例二最大的长度变形为0.301 9/100000,而高速铁路测量要求长度变形小于1/100 000。因此,将斜轴墨卡托投影应用于高速铁路测量具有明显优势。

(3)结合图3、表1和表2来看,随着距离线路中心线的垂直距离的增加,斜轴墨卡托投影的长度变形在增大。因此,选择合适的中心线大地方位角很重要,确保各测点距离投影中心线的平均垂直距离(即y值)更小,从而更好地控制投影引起的长度变形。