基于GMM 的AMR-NB 与G.729A 之间的LSP 参数转码方法

刘张宇，鲍长春，邱建伟，徐昊

（北京工业大学 电子信息与控制工程学院 语音与音频信号处理实验室，北京 100124）

1 引言

AMR-NB[1](adaptive multiple rate-narrow band)是3GPP(3rd generation partnership project)制订的语音压缩标准，现广泛应用于 WCDMA(wideband code division multiple access)和TDS-CDMA(time division-synchronous code division multiple access）等第 3代移动通信系统中。G.729[2]是 ITU（international telecommunication union）于1995年制定的语音编码标准，G.729A[3]是G.729的低复杂度版本，现主要应用于语音压缩与VoIP(voice over internet protocol)等通信系统。这 2种基于CELP[4](code-excited liner prediction)的语音编码技术在当今移动通信系统和网络通信系统中的作用越来越重要。为了实现不同供应商之间通信设备的兼容与互通，需要在这2种不同语音编码标准之间进行转码工作。

在基于CELP的AMR-NB和G.729A语音转码中，LSP参数转码是转码算法流程的第一步，也是整个语音转码算法的核心部分之一，基音参数，代数码数以及增益的转码均建立在 LSP参数转码的基础之上，因此，LSP参数转码效果将直接影响最终合成的语音质量。目前在LSP参数转码中应用最为广泛的方法是直接转码（DTE，decode then encode）模式，这种传统的码流转换方案具有2个缺点：1）运算量大；2）由于二次压缩造成语音失真度加大，降低了合成语音质量[5]。为了解决DTE方法带来的弊端，国外学者提出了利用直接参数转换的方法[6,7]来实现这2种编码标准之间的LSP参数转码，然而，LSP参数转码虽然能够有效降低计算复杂度，但仍然存在二次量化失真，因此，需要找到一种更加有效的 LSP参数转码算法以提高转码语音质量。

本文对高斯混合模型（GMM,Goussian mixture model）进行了分析研究，并将其应用到了AMR-NB与G.729A之间的LSP参数转码算法中。该方法利用大量训练语音数据，通过EM迭代算法进行高斯混合模型参数的估计，最后得到LSP参数转码函数。通过大量实验，本文分析了训练数据量、GMM数量、不同初始化方法的选取、收敛门限的限定和协方差矩阵限定与转码算法性能的关系，并得出了相应的结论。本算法在保证语音质量的情况下，极大地降低了计算复杂度和存储空间。

2 GMM概述

GMM 是一种多维概率密度函数，常用来表示未知概率分布数据的分布函数，它在本质上是单状态的HMM模型，其核心思想是用多个高斯分布的概率密度函数的组合来描述特征矢量在概率空间的分布状况[8]。根据统计理论，若干个高斯概率密度的线性组合可以逼近任意分布，因此GMM能够很好地描述各种形式的语音特征统计分布及其特性。下面介绍GMM的基本原理。

2.1 GMM的参数描述

GMM是由M个服从高斯分布的概率密度函数的加权组合而成的，其中每个高斯概率密度函数可以看作一个类，如图1所示。

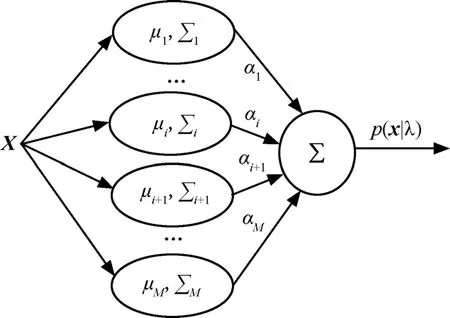
图1 GMM组成示意图

其表达式为

式(1)中x是D维的特征向量，iα是各高斯函数的混合权重，必须满足的限制，μ是高斯分布的均值向量，Σ是高斯分布的协方差矩阵，M是混合高斯模型中高斯函数的数量。 N(x; μi; Σi)为M个D维的高斯概率密度函数，计算公式如下所示：

一个GMM可以由均值矢量、协方差矩阵和混合权值等参数进行描述，通常用λ来表示这些参数的集合，如式(3)所示：

应用式（3），可将式（1）改写为

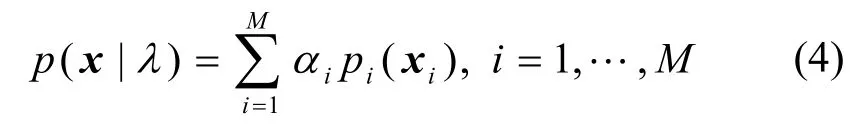
其中

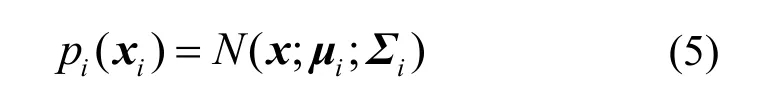
2.2 GMM的参数估计(EM算法)

在语音的LSP参数转码中应用GMM需要解决一个问题，即通过输入码流x来求得模型参数λ，使得p(x|)λ达到最大值，从而求得LSP转码函数。这种优化准则即为最大似然估计准则(MLE)，而如何调整模型参数λ，使p(x|)λ达到最大值，也就是GMM的训练问题。

本文采用EM迭代算法进行GMM参数训练。该算法主要分为下面2个步骤。

1) E步，即预估参数。根据所有训练数据来估计高斯混合模型的混合权值、均值向量和协方差矩阵等参数。

2) M步，即最大化。从上一步得到的估计结果中，根据最大似然准则重新估算模型参数值，直到参数值达到最佳为止。

其中EM迭代算法中使用的公式如下所示[9]：

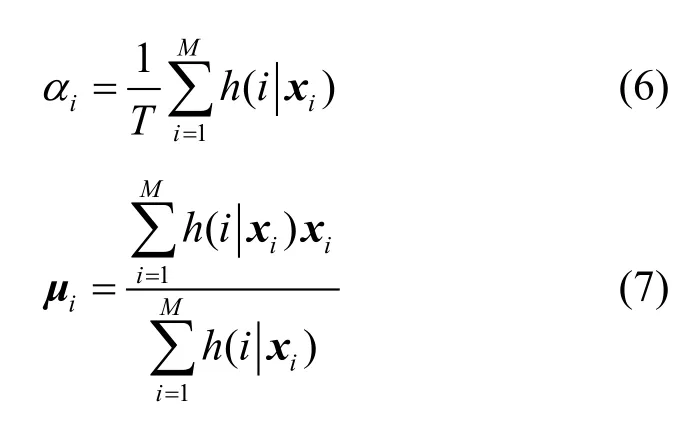
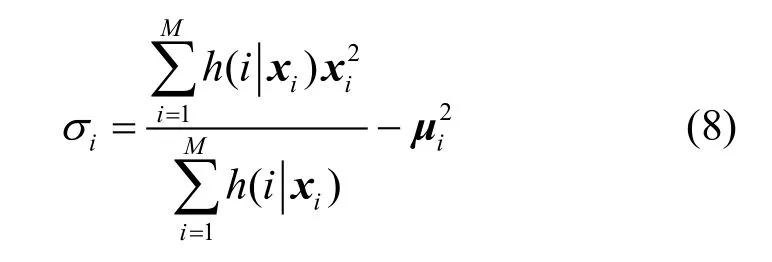
下面给出GMM的训练流程，如图2所示。

图2 GMM训练流程图

在进行 EM 算法之前，首先需要对参数集λ={αi,μi,Σi}进行初始化，本文采用的是K均值方法进行参数值初始化，即对训练数据中的所有特征矢量求均值和方差，作为初始均值和方差，初始权重设为相等权重，即α=1/M。利用EM迭代算法求出新的，并与前一次得到的进行比较，如果比较得到的差值小于一个设定的门限δ，则迭代结束，即可求得相对应的 GMM 参数集λ={αi, μi,Σi}。

3 基于GMM的LSP参数转码

3.1 LSP参数转码函数的建立和求取

如何建立和求取基于GMM的LSP参数转码函数是LSP转码中的核心问题。图3给出了转码函数F(x)的建模框架。

图3 基于GMM的LSP转码函数训练过程

首先将语音训练数据分别通过 AMR-NB与G.729A的编码端，得到2组LSP参数向量，定义为X和Y，以最小均方误差准则，对X和Y根据最大似然准则进行联合高斯混合模型训练，即得到转码函数F(x)。将F(x)引入到转码算法中，当源端的LSP参数码流通过F(x)后，即得到目标端的LSP参数，从而完成LSP转码。接下来利用联合高斯分布的条件期望预测方法[10]对转码函数F(x)进行数学建模，如图4所示。

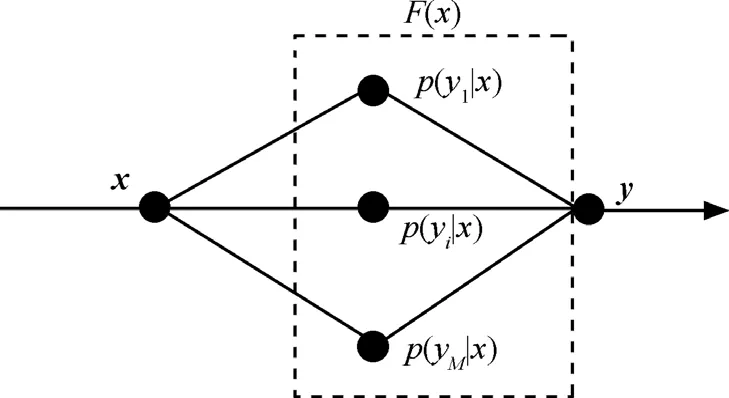
图4 基于加权后验概率的转码函数建模

源端的一组LSP参数X经过转码函数得到目标端的一组LSP参数Y，由于LSP参数具有独立性，因此X与Y是按序一一对应的，根据后验概率的思想，转码函数是M个加权后验概率的组合，其数学表达式如下：

根据贝叶斯公式，得到

为了求解式（10）中的未知参数，需要对2端LSP参数进行联合高斯混合模型训练[11]。首先把按时间对齐的AMR-NB端LSP参数和G.729A端LSP参数合在一起，如式（12）所示：

式(12)中，N是训练数据的数量，D是LSP参数的维数。然后利用 EM 迭代算法对矢量集Z2N×D进行GMM训练，得到GMM参数集λ{αi,μi,Σi}，其中协方差矩阵和均值分别表示为

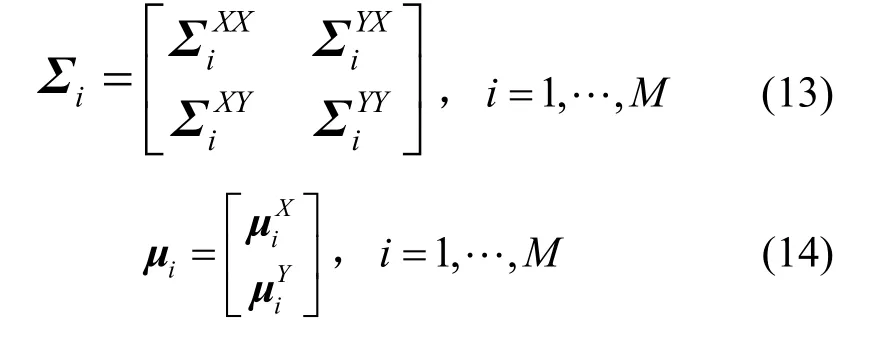
将式(2)、式(11)、式(13)、式(14)代入式(1)即可求得F(x)，即求得目标端LSP参数，完成LSP参数转码。

3.2 GMM在LSP参数转码应用中的问题

GMM参数在LSP参数转码中的应用中最关键的部分是参数的迭代估计，而在EM迭代算法中需要注意训练数据的选择和模型参数的选择等问题。下面通过一系列实验对这些问题进行详细的分析。本文实验均以AMR-NB 10.2kbit/s模式与G.729A转码为例。

3.2.1 训练数据量对转码结果的影响

1) 不同训练数据量对合成语音质量的影响。

由于GMM是一种概率统计模型，因此训练数据量的大小对建模效果有较大的影响，从而间接影响转码效果。首先取 GMM 数为 32，分别采用从8s到约26min不同时长的NTT数据库标准语音作为测试数据进行GMM训练，并对6句中文语音（男女声各 3句）进行转码实验，得到了平均的客观MOS 分值[12,13]。

如图5所示，当高斯混合函数个数一定时，转码语音质量随着训练数据集的增大而提高，但在训练数据量超过2万帧之后，继续加大训练数据对语音质量的提高不再有明显作用。另外，在基于GMM的 LSP参数转码算法中，在测试语料相同的条件下，AMR-NB向G.729A转码的MOS分要略高于G.729A向AMR-NB，这种情况与DTE以及传统参数转码算法相似。

2) 不同训练数据量对计算复杂度的影响。

LSP参数是通过转码函数F(x)进行转码的，转码函数F(x)的构建是通过对 GMM 参数进行训练完成的，而GMM的EM参数估计并不依赖于源LSP码流，是预先完成、独立于转码算法之外的。因此，整个GMM训练过程对转码算法的计算复杂度没有影响，训练数据集的增加也与转码计算复杂度无关。

图5 训练数据量的大小对转码客观MOS分的影响

3.2.2 GMM数选取对转码结果的影响

1) 不同GMM个数对平均谱失真(SD,spectual distortion)的影响。

谱失真的定义如下：

图6 LSP参数转码随GMM数增加的谱失真变化曲线

从图6中可以看到随着GMM个数的增加，LSP参数转码谱失真逐渐下降，最后趋向于一个极值。另外，基于DTE方法的AMR-NB10.2kbit/s模式向G.729A转码的谱失真是2.683dB，因此，当GMM个数大于等于16时，本LSP参数转码方法产生的谱失真小于DTE转码方法。

2) 不同GMM个数对合成语音质量的影响。

GMM是由具有M个混合成分的高斯密度函数来进行线性叠加的，因此高斯模型的阶数，即高斯密度函数的个数的大小与基于GMM的LSP参数转码效果直接相关。基于GMM的LSP参数转码算法是利用 GMM 对线谱频率参数进行拟合，因此，在理论上M越大，声道谱参数包络就拟合得越精确，转码性能也就越好。本实验以AMR10.2kbit/s转码速率为例，首先利用 76 800帧的NTT数据库标准语音作为训练数据，分别采用5种从小到大的不同的混合数进行GMM训练，并对6句中文语音（男女声各3句）进行转码实验，得到了平均的客观MOS分值，GMM个数对LSP参数转码后合成语音质量的影响实验结果图7所示。

图7 GMM数大小对转码语音质量的影响

从图7可以看出，在训练数据量一定的条件下，一般地，转码语音质量随着GMM数的增加而提高，但在混合模型达到256时，转码性能低于 128个混合模型数，也就是说，在 LSP参数转码的实际应用中，GMM训练出现了过训练现象。因此单从GMM数对LSP参数转码质量的影响来看，存在一个 GMM 的个数能够对应最优的转码语音质量。经过实验比较，取 GMM 个数为128。

3.2.3 EM算法中迭代次数的分析与收敛门限的确定

前文中已经讨论了EM迭代算法的流程，应用最大似然法来获得所要最大化的目标GMM参数集λ需要预先设定一个门限值δ，而这个门限值与EM 迭代算法的迭代速度和收敛精度密切相关，因此，选择一个合适的δ是比较重要的。由于GMM 个数同样影响迭代速度，因此本实验对门限值和 GMM 数进行联合分析。在本实验中，GMM 数分别取 8，16，32，64，训练数据为 24句NTT标准语音库语音，每句时长为8s。实验结果如图8所示。

从图8中可以看到，迭代次数是由收敛门限值和GMM数2个因素共同决定的。当GMM数较少时，迭代次数主要取决于收敛门限的取值，这是因为少量的GMM不足以准确描述谱参数特征，需要更高的精度来保证GMM的准确性。当GMM数足够多时，在本实验中即 GMM数达到64时，大量的GMM只需较少次数的迭代便可以满足收敛门限的要求。在实际应用中，出于对计算复杂度的考量，GMM数不能取值过大，因此，需要通过确定较高的收敛门限来保证精度，在本文中取门限值δ为10-6。

图8 门限值和GMM数与迭代次数的关系

4 实验结果

为了验证本文所提算法的有效性，在主观A/B听力测试与客观MOS分测试中，LSP参数采用基于GMM的LSP参数转码技术进行转码,而基音参数、代数码数以及增益采用 DTE转码方式进行转码。

4.1 主观A/B听力测试

本实验采用A/B听力测试方法对转码语音进行了主观测试。测试语音由24句组成，每句长8s，分别由2男2女4个说话人发音。6名测听人员分别对LSP经DTE转码的语音和经GMM转码的语音进行主观测听，并得到以下主观偏好结果，如表1所示。

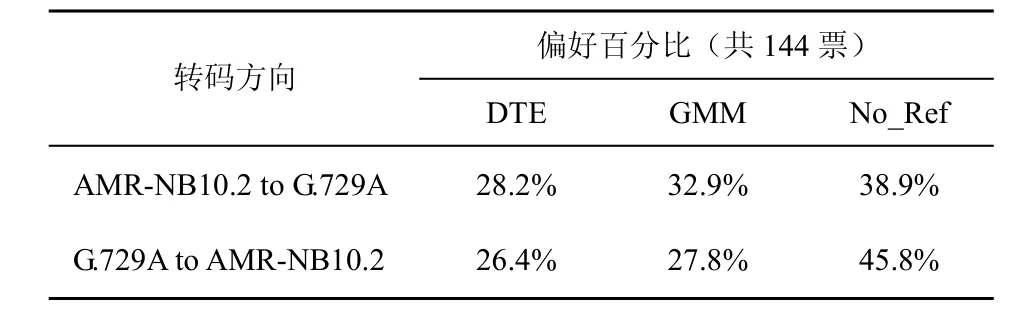
表1 LSP转码语音的主观A/B听力对比

从表1中可以看到，在AMR-NB 10.2kbit/s与G.729A之间的转码中，基于GMM的LSP转码主观听力质量不次于DTE的LSP转码方法。

4.2 客观MOS分测试

本实验使用 ITU-T P.862.1所规定的MOS_LQO[14]为客观语音质量的衡量标准。实验选取NTT标准语音数据库的96句中文语音作为测试数据源，一共4男4女8位说话人，每人讲12句话，每句8s时长，对于AMR-NB来说是每句话400帧，对于G.729A来说是每句话800帧。以AMR-NB 10.2kbit/s模式向G.729A转码为例，与DTE转码模式进行比较，实验测得的MOS分结果如表2所示。

表2 LSP转码语音的MOS分比较

从表2中的MOS分值中可以看到，在男声测试语音中，LSP 2种转码算法的质量非常接近；在女声测试语音中，基于GMM的LSP转码语音质量略低于DTE方法；在所有语句中，GMM方法的平均MOS分与DTE方法比较接近，表明转码语音质量在可接受的范围之内。

4.3 复杂度结果

在本实验中预设高斯混合模型值为128，基于GMM的LSP转码算法与基于DTE的LSP转码算法的计算复杂度与空间复杂度对比如表3所示。

表3 LSP转码方法的复杂度比较

从表3中可以看到，基于GMM的LSP转码方法与 DTE方法相比，极大地降低了计算复杂度和空间复杂度，取得了比较好的结果。

5 结束语

本文主要概述了高斯混合模型的定义和基本原理，详细介绍了高斯混合模型的参数估计算法——EM 迭代算法，提出并实现了基于 GMM 的AMR-NB与G.729A之间的LSP参数转码算法，以10.2kbit/s转码速率为例，分析了GMM在LSP参数转码中的几个实际应用问题，最后给出了实验结果。实验结果表明，基于GMM的LSP转码方法能够在保证合成语音质量的前提下，极大地降低计算复杂度和空间复杂度。GMM在LSP参数转码应用中的有效性，为GMM在其他参数转码中的应用提供了重要的借鉴意义。

[1] ETSI EN 301 704 V7.2.1 Adaptive Multi-Rate(AMR)Speech Transcoding[S].2000.

[2] ITU-T G.729:Coding of Speech at 8kbit/s Using Conjugate Structure Algebraic Code Excited Linear Prediction(CS-ACELP)[S].1996.

[3] ITU-T G.729A: Educed Complexity 8kbit/s CS-ACELP Speech Codec[S].1996.

[4] 鲍长春.数字语音编码原理[M].西安:西安电子科技大学出版社,2007.BAO C C.Principles of Digital Speech Coding[M].Xi’an: Xidian University Press,2007.

[5] 邱建伟,鲍长春,徐昊等.基于CELP编码模型的参数转码技术[J].电声技术,2009,(4):84-87.QIU J W,BAO C C,XU H,et al.Parameter transcoding techniques based on CELP speech coding[J].Audio Engineering.2009(4): 84-87.

[6] OTA Y,SUZUKI M,TSUCHINAGA Y,et al.Speech coding translation for IP and 3G mobile integrated network[A].IEEE International Conference on Communications[C].New York: IEEE Press,2002.114-118.

[7] GHENANIA M,LAMBLIN C.Low-cost smart transcoding algorithm between ITU-T G.729(8kbit/s) and 3GPPNB-AMR(12.2kbit/s)[A].European Signal Processing Conference[C].Vienna: EUSIPCO Press,2004,(3): 1681-1684.

[8] 赵永刚,唐昆,崔慧娟.基于Gaussian混合模型的LSF参数量化方法[J].清华大学学报(自然科学版),2006,46(10): 1727-1730.ZHAO Y G,TANG K,CUI H J.Quantization of LSF parameters using a Gaussian mixture model[J].J Tsinghua University(Sci & Tech),2006,46(10): 1727-1730.

[9] 吴金池.语音辩识系统之研究[D].台湾国立中央大学,2003.9-17.WU J C.Research on Speech Recognition System[D].Taiwan,China:National Central University,2003.

[10] KAIN A B.High Resolution Voice Transformation[D].Oregon Health and Science University,2001.36-54.

[11] 康永国,双志伟,陶建华等.高斯混合模型和码本映射相结合的语音转换算法[A].第八届全国人机语音通讯学术会议[C].2005.293-297.KANG Y G,SHUANG Z W,TAO J H,et al.Speech transform algorithm based on Gaussian mixture model and codebook mapping[A].NCMMSC2005[C].2005.293-297.

[12] 付强.语音的参数表示和质量客观评价研究[D].西安电子科技大学,2000.46-66.FU Q.Research on Parameter Representation and Objective Quality Assessment of Speech[D].Xi’an: Xidian University.2000.46-66.

[13] ITU-T P.800.1:Mean Opinion Score(MOS) Terminology[S].2003.

[14] ITU-T P.862.1: Mapping Function for Transforming P.862 Raw Result Scores to MOS-LQO[S].2003.