高精度Σ-ΔADC中的数字抽取滤波器设计

吴笑峰，刘红侠，李迪，胡仕刚，石立春

(1. 湖南科技大学 信息与电气工程学院，湖南 湘潭，411201；2. 西安电子科技大学 微电子学院 宽禁带半导体材料与器件教育部重点实验室，陕西 西安，710071)

Σ-ΔADC现已成为高精度ADC[1]设计的一种切实可行的解决方案。Σ-ΔADC由Σ-Δ调制器和抽取滤波器组成，Σ-ΔADC中调制器的基本原理是过采样和噪声整形。在Σ-ΔADC中，需要采用数字抽取滤波器对调制器的输出数据进行抽取，将原来的过采样频率降低到奈奎斯特采样率，并同时将模拟信号转换成数字信号。数字抽取滤波器的主要作用是移除量化噪声，降低采样频率和抗混叠。本文的主要目标是设计1个应用于18位二阶Σ-ΔDC中的数字抽取滤波器。数字抽取滤波器的性能参数如下：输入信号采样频率为6.144 MHz，输出信号采样频率为奈奎斯特率即48 kHz，降采样率为128，通带频率为21.77 kHz，阻带增益频率为26.23 kHz，通带波纹系数为±0.01 dB，阻带增益衰减120 dB。由于数字抽取滤波器对整个Σ-ΔADC的面积和功耗有非常重要的影响[2-4]，在此，本文作者采用多级结构[5-7]的实现形式，并对各级滤波器的面积和功耗进行最大程度优化。

1 整体结构

多级结构可以极大地减小滤波器的阶数，因此，本文采用多级结构(如图1)来达到降采样的目的。设计中，同时根据最终的设计目标，采用一些特殊的滤波器来进一步减小面积和功耗。

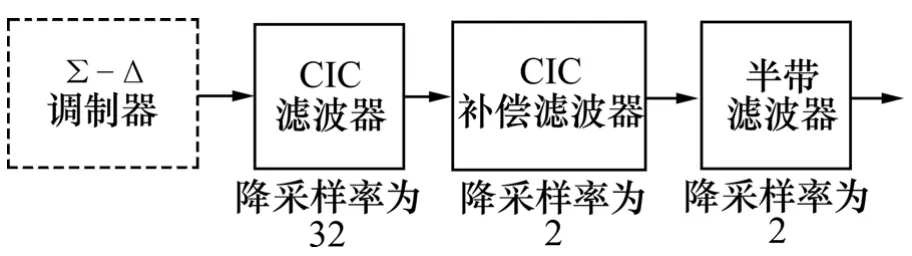
图1 数字抽取滤波器结构Fig.1 Structure of digital decimation filter

在设计Σ-ΔADC时，由于第1级抽取系数比较大，通带只占输出抽样频率的很小部分，因此，第1级滤波器可以采用 1种特殊的滤波器即级联梳状(Cascade of integrators comb, CIC)滤波器[8]。它可以大大减小第1级滤波器的阶数，也使得整体设计简化很多。虽然第1级梳状滤波器的面积很小，但梳状滤波器在通带内有衰减，这就需要在第2级补偿带内衰减，因此，第2级采用CIC补偿滤波器。CIC补偿滤波器实际上是1个FIR滤波器，其降采样率为2。第3级采用半带滤波器。半带滤波器的一半系数为 0，另外一半系数对称，这就降低了第3级滤波器阶数，第3级滤波器降采样率为 2。通过分析可以得到各级滤波器的输入输出采样频率、通带、阻带边界频率及降采样率，如表1所示。

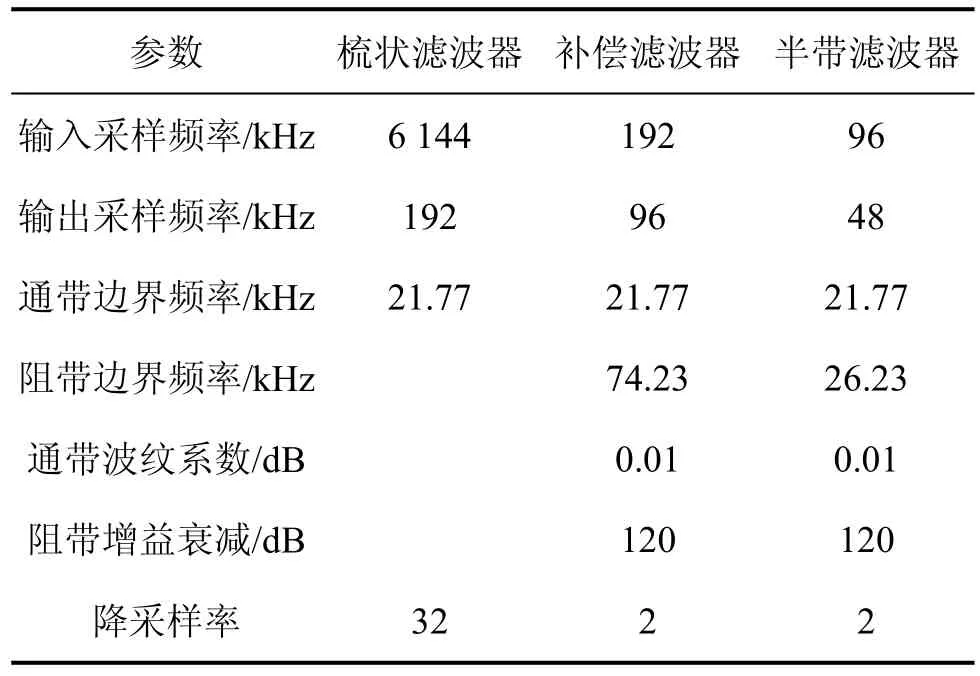
表1 各级滤波器的指标Table 1 Performance of filters at various levels

2 数字抽取滤波器设计

2.1 梳状滤波器的设计

梳状滤波器是一种在高速抽取或差值系统中非常有效的单元，主要用于无线通信和Σ-ΔADC中。采用多级级联梳状滤波器的结构来优化第1级滤波器的频率响应。CIC滤波器的传递函数为：

其频率响应为：

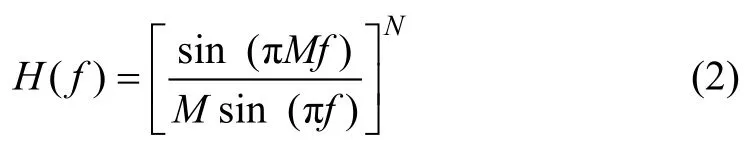
其中：M为梳状滤波器的降采样率；N为梳状滤波器级联的个数，它的频率响应如图2所示(以M=8为例)。一般来说，在对L阶、过采样率为M的Σ-Δ模拟调制器进行降频时，梳状滤波器的级联个数要达到L+1以上，才能产生足够的噪声衰减[9]。由图 2可知：梳状滤波器在通带内会衰减，因此，第2级滤波器用补偿滤波器来实现。设定梳状滤波器的输出频率为奈奎斯特采样率的4倍，其原因是：若输出采样频率太高，则会增大后级滤波器的阶数，进而增大面积和功耗；若输出采样频率太低，则相当于增加了梳状滤波器自身的“瓣数”，而通带边界不变，很明显，通带频率Fp处的衰减会增大，同时，也使得通带边界“靠近”阻带边界，增大通带内噪声。

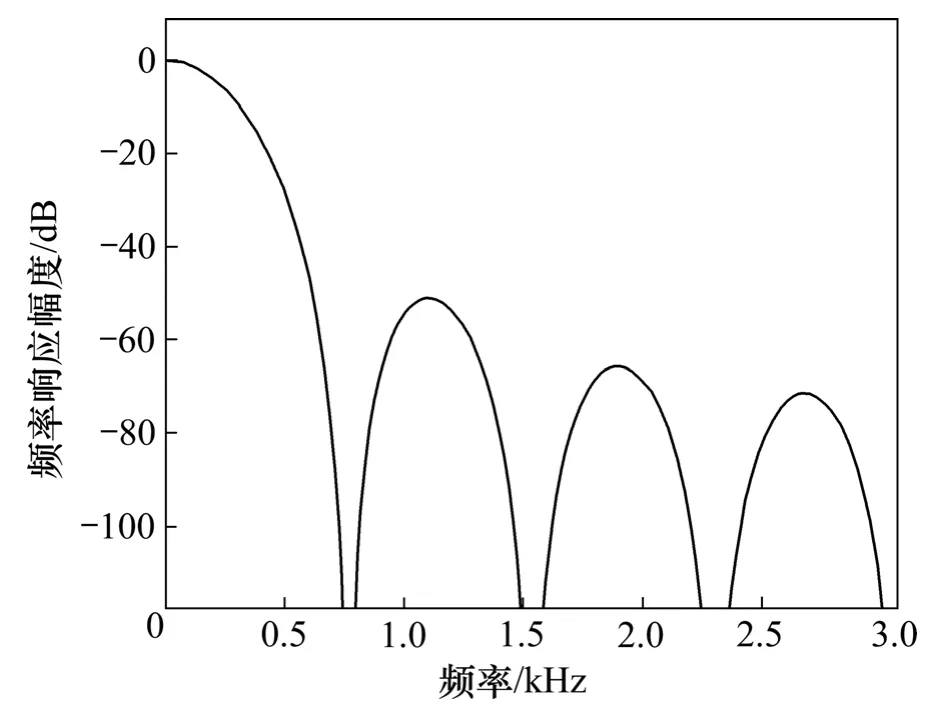
图2 级联梳状滤波器的频率响应(M=8, N=4)Fig.2 Frequency response of CIC filter (M=8, N=4)

根据上面分析，确定本文的级联梳状滤波器的结构为：级联个数N=5，降采样率M=32。

2.2 CIC补偿滤波器的设计

为了补偿CIC滤波器对通带的衰减，第2级采用CIC补偿滤波器。CIC补偿滤波器是 1种 FIR滤波器。设计补偿滤波器就要根据FIR滤波器的设计方法进行设计。本文采用切比雪夫最佳逼近法来设计CIC补偿滤波器。对这种结构进行设计时，一般是参考Mcclallan的 Remez算法进行迭代，求出滤波器的系数[10]。可以调用Matlab中的Remez函数来设计，也可调用Matlab8.0 filter design toolbox中的CIC补偿滤波器模型来设计[11]。CIC补偿滤波器频率响应如图3所示。从图3可见：补偿滤波器在通带内有凸起，能起到一定的补偿作用，但需要和CIC滤波器级联来看最终的补偿结果。

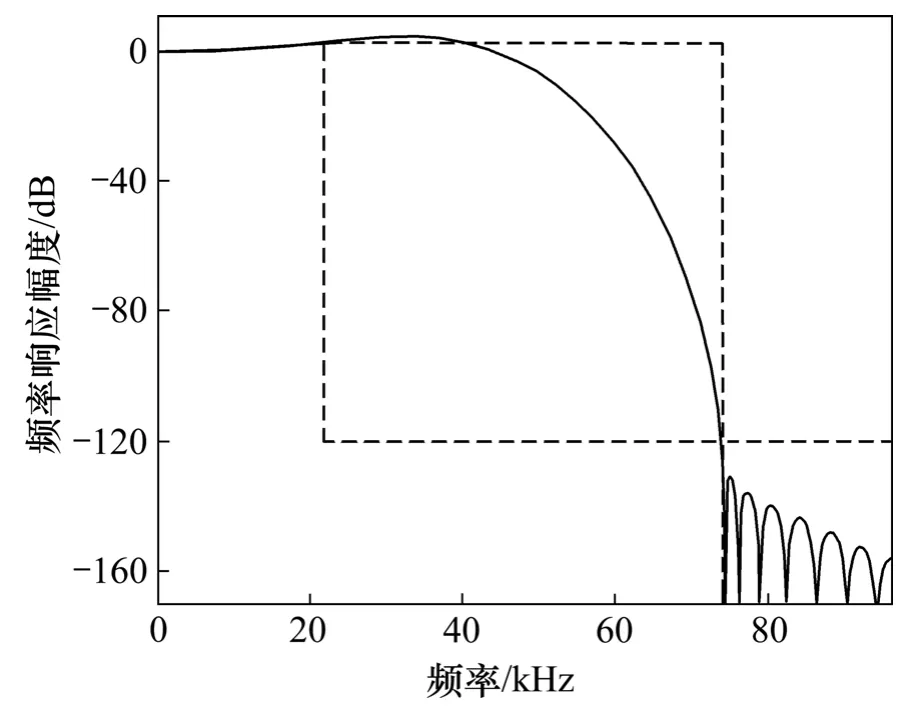
图3 CIC补偿滤波器的频率响应Fig.3 Frequency response of CIC compensation filter

根据表1中的CIC滤波器设计参数：降采样率为32，微分延时(硬件设计时的反馈延时)为1。据补偿滤波器的边界频率和降采样率来设计相关的补偿滤波器，可以得到相应的补偿滤波器。它与CIC滤波器以及两者级联(Cascade filter)以后的频率响应如图 4所示。从图4所示CIC滤波器和CIC补偿滤波器的级联结果来看，求得的补偿滤波器可以很好地补偿 CIC filter在通带内的衰减，能达到设计的目标。

由Matlab运算得到CIC补偿滤波器，它共有22阶，各阶系数见表2。从表2可以看出：CIC补偿滤波器的系数是对称的，在其22阶的系数中，只有11个不重复的系数。在硬件实现时，这个特点可以使本级滤波器的面积减小一半。

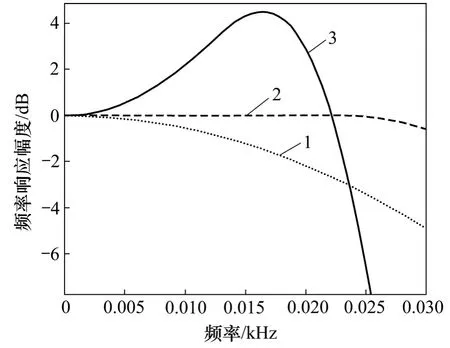
图4 CIC滤波器、CIC补偿滤波器和Cascade滤波器的频率响应Fig.4 Frequency response of CIC filter, CIC compensation filter and Cascade filter

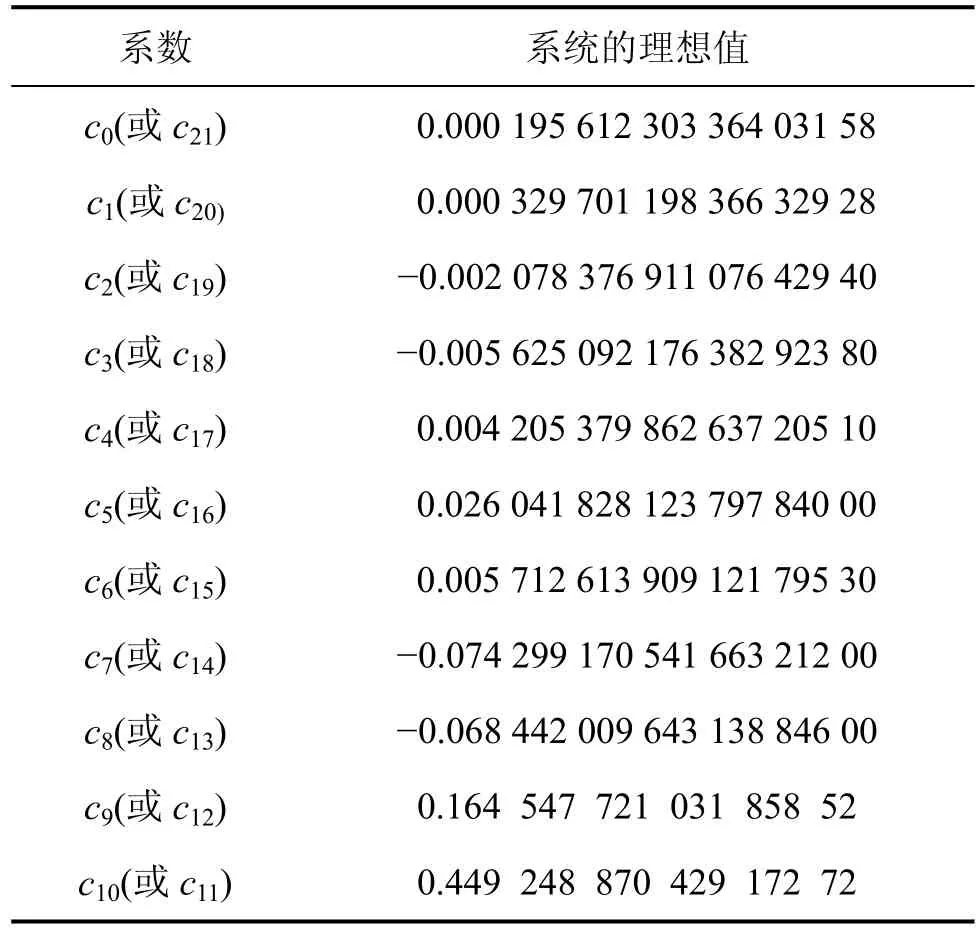
表2 CIC补偿滤波器的系数Table 2 Coefficient of CIC compensation filter

2.3 半带滤波器的设计

在设计最后一级滤波器时，发现只需要2倍降采样的滤波器即可，而半带滤波器可以满足这种要求，它的近一半系数为 0。因此，相对于能达到同样效果的普通FIR滤波器来说，半带滤波器乘法单元减少一半。因此，最后一级滤波器采用半带滤波器[12]。半带滤波器的频率响应为：

其半带滤波的单位脉冲响应为：

其中：N为奇数。从式(3)可以看到：当n-(N-1)/2为偶数时，滤波器的系数h(n)为 0，而且半带滤波器也属于FIR滤波器。FIR滤波器的单位脉冲响应有对称性[13]，因此，半带滤波最多只有N/4+1个不重复系数。与补偿滤波器一样，半带滤波器也属于FIR滤波器。考虑到半带滤波器的特点，在用切比雪夫逼近法设计半带滤波器时，可以简化设计。假定需要设计1个长度为N的半带滤波器，当(N-1)/2为奇数时(若为偶数，则h(0)=h(n)=0，相当于1个N-2的半带滤波器)，设计的通带边界、阻带边界和波纹系数分别为ωp，ωc和δp。首先用等波纹设计1个(N-1)/2的普通FIR滤波器g(n)，其通带波纹系数为2δp，通带边界系数为2ωp。由于2ωc＞π，故可以将这个g(n)的阻带边界系数设为π。定义：

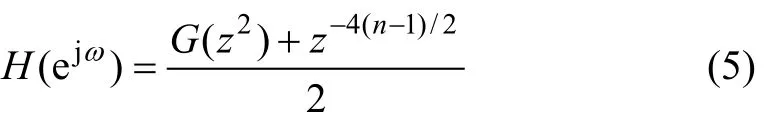
则有

其中：n=0, 1, …,N-1。根据G(n)的参数求出g(n)，然后，根据公式(6)得到h(n)的系数，它们的频率响应如图5所示。

采用Matlab8.0/simulink/filter design toolbox中的Halfband滤波器模型设计更方便。最终得到的159阶Halfband滤波器，系数的有效数为40个。

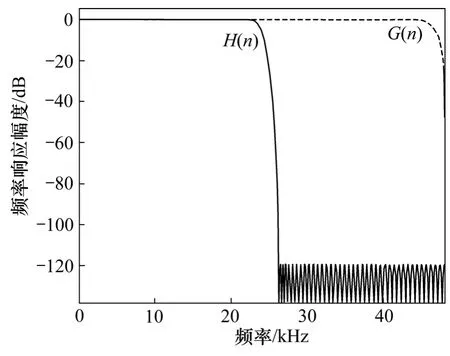
图5 G(n)与H(n)的频率响应Fig.5 Frequency response of G(n) and H(n)

3 芯片测试结果

整个芯片采用Chartered 0.35 μm CMOS工艺实现，工作电压为5 V。

模拟调制器部分和数字降采样滤波器部分使用隔离环进行隔离，防止数字部分的噪声影响模拟电路部分。CIC补偿滤波器和半带滤波器的系数采用 CSD(Canonic signed digit)码实现，以实现滤波器系数最大程度的优化。电路使用移位器和加法器实现。使用逻辑分析仪对模拟调制器输出测试端口的信号进行数据采集，并使用 MATLAB软件进行频谱分析，可得调制器输出频谱图如图6所示。从图6可见：当输入信号为-4 dB(频率为6 kHz)时，在带宽24 kHz内，信噪失真比 (SNDR)为102.8 dB，有效位数为16.79位。使用相同的方法，经过降采样滤波，所得信号频谱如图7所示。从图7可见：所设计的数字降采样滤波器通带截止频率为21.77 kHz，过渡带为4.5 kHz，通带波纹系数为±0.01 dB，阻带增益衰减120 dB。对芯片的测试结果表明：当工作电压5 V时，所设计的抽取滤波器部分功耗仅为49 mW，面积约为0.6 mm×1.9 mm。

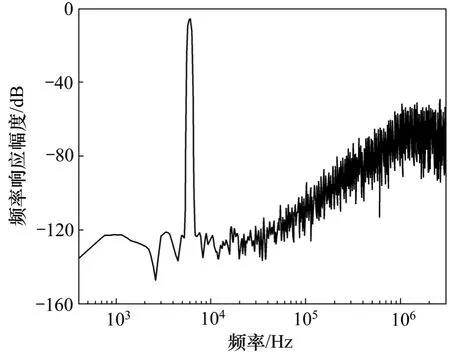
图6 调制器的测试频谱图Fig.6 Testing frequency spectrum of modulator

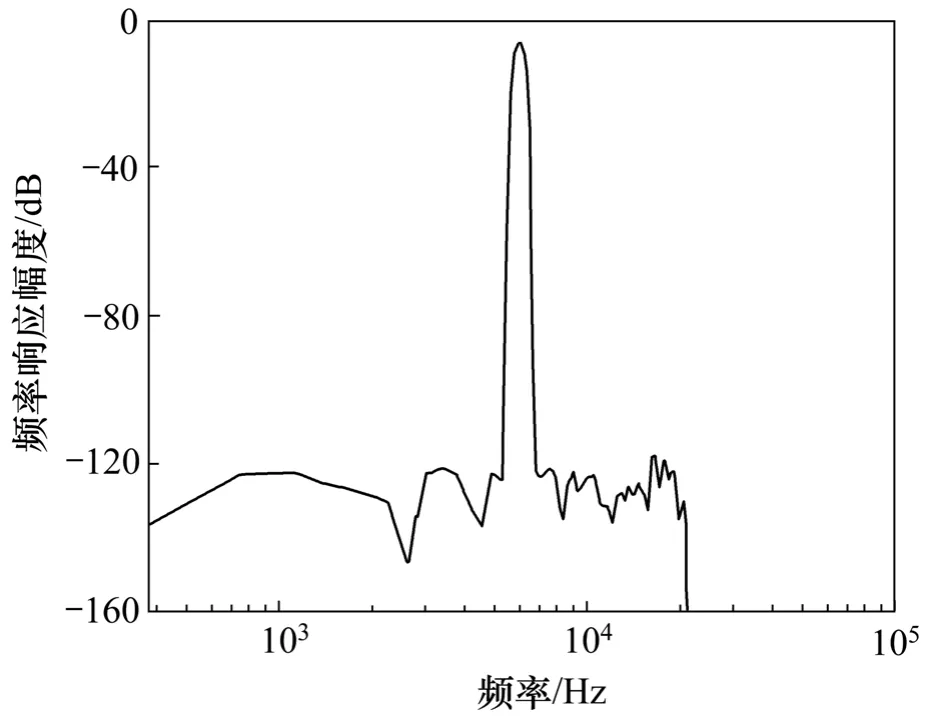
图7 数字滤波器输出频谱图Fig.7 Output frequency spectrum of digital decimation filter

4 结论

(1) 采用Chartered 0.35 μm CMOS 工艺实现了一种用于高精度Σ-ΔADC多级多采样率结构的数字抽取滤波器。该数字抽取滤波器的带宽为21.77 kHz，输入采用频率6.144 MHz，降采样率为128。对滤波器的系统结构进行了设计，在确定采用多级结构之后，分别对各级滤波器的结构、阶数以及系数进行优化设计。

(2) 在满足滤波器的设计目标下，采用了最优的选择。测试结果表明，数字降采样滤波器组的设计符合预期的要求。

[1] 凌玉华. 高速高精度模/数转换的微机动态轨道衡[J]. 中南工业大学学报: 自然科学版, 1999, 30(6): 623-625.LING Yu-hua. A microcomputerizer dynamic railway scale with high-speed and high-glass accuracy A/D conversion[J]. Journal of Central South University of Technology: Natural Science,1999, 30(6): 623-625.

[2] Hogenauer E B. An economical class of digital filters for decimation and interpolation[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1981, 29(2): 155-162.

[3] Chen L, Zhao Y F, Gao D Y, et al. A decimation filter design and implementation for oversampled sigma delta APD converters[C]//Proceedings of 2005 IEEE International Workshop on VLSI Design and Video Technology. Suzhou, 2005:55-58.

[4] Ren S, Siferd R, Blumgold R, et al. Hardware efficient FIR compensation filter for delta sigma modulator analog to digital converters[C]//48th Midwest Symposium on Circuits and Systems. Covington, Kentucky, 2005: 1514-1517.

[5] Brandt B P, Wooley B A. A low-power area efficient digital filter for decimation and interpolation[J]. IEEE Journal of Solid-state Circuits, 1994, 29(6): 679-687.

[6] Goodman J, Carey M J. Nine digital filters for decimation and interpolation[J]. IEEE Trans Acoust, Speech, Signal Processing,1997, 25(3): 121-126.

[7] Coffey M. Optimizing multistage decimation and interpolation processing[J]. IEEE Signal Process Lett, 2003, 10(4): 107-110.

[8] Aboushady H, Mehrez H. Efficient polyphase decomposition of comb filters in SD analog-to-digital converters[J]. IEEE Trans Circuits Syst Ⅱ: Analog and Digital Signal Process, 2001, 48:898-903.

[9] Candy J C. Decimation for sigma delta modulation[J]. IEEE Trans Comm, 1986, 34(1): 72-76.

[10] Crochiere R E, Rabiner L R. Interpolation and decimation of digital signals: A tutorial review[C]//Proceeding of the IEEE.Houston, 1981, 69: 300-331.

[11] Maulik P C, Chadha M S, Lee W L. A 16-bit 250-KHz delta-sigma modulator and decimation Filter[J]. IEEE Journal of Solid-state Circuits, 2000, 35: 458-467.

[12] Vaidyanathan P P, Nguyen T Q. A “TRICK” for the design of FIR half-band filters[J]. IEEE Trans Circuits and Systems, 1987,34(3): 297-301.

[13] Lu W, Hinamoto T. Design of FIR filters with discrete coefficients via polynomial programming: towards the global solution[C]//IEEE ISCAS. New Orleans, 2007: 2048-2051.