新型双向硬密封旋球阀多学科设计优化

鄂加强 ，李志鹏，袁丁，滕达，雷吉平，龚金科

(1. 湖南大学 机械与运载工程学院，湖南 长沙，410082；2. 湖南泵阀制造有限公司，湖南 长沙，410007)

阀门是管道流体输送系统中应用最广泛、最重要的执行机构或者控制元件[1-3]，具有接通或截断流体通路、调节与节流、防止倒流、调节压力或释放过剩的压力等功能，可以控制空气、水、各种腐蚀性化学介质、泥浆、液态金属和放射性物质等各种类型流体的流动，在国民经济各个部门得到广泛应用。新型双向硬密封旋球阀具有结构紧凑、供水效率高、成本低廉的优点，广泛应用于有压供水管道系统[4]。然而，在新型阀门开发能力方面，水力模型少，在强度、刚度、启闭、振动和可靠性设计方面还存在一定的差距。尽管国外已将计算流体力学、有限元结构与旋转动力学分析、新型的信息管理与应用技术应用于阀门的设计、应用与实际操作[4-6]，但阀类机械的设计还停留在“设计—试制—试验—改进”的阶段，实用性较差；虽然一些研究者对存在的问题和故障现象提出了解决办法，但都未从根本上解决存在的问题[7-10]。目前，新型双向硬密封旋球阀传统的优化设计主要集中考虑改变新型双向硬密封旋球阀结构设计，或者只考虑强化结构强度的影响，因此，造成新型双向硬密封旋球阀优化设计结果不理想。随着人们对产品性能的要求越来越高以及热动力系统复杂程度的提高，近些年来出现的多学科设计优化(Multidisciplinary design optimization，简称MDO)[11-13]为新型双向硬密封旋球阀优化设计提供了新的研究思路。

1 新型双向硬密封旋球阀工作原理

新型双向流旋球阀总体结构类似蝶阀结构，分为阀体总成(包括阀体和阀座)和阀板总成(阀板、阀杆和阀杆端密封件、驱动机构)。阀板密封面类似球阀，为正球面，相当于球体两端直接切除余下的部分。阀板固定于阀杆上，在外部驱动机构作用下，围绕阀杆轴线转动，作为阀门启、闭件。阀座不与阀体连为一体，为单独的零件，在介质作用下可沿阀体轴线移动。阀座密封面为圆环锥面，阀门关闭时密封面为线接触密封。阀芯的密封面为三次曲面，阀座的密封面为一次圆锥面。在密封点处，阀座面实际上是阀芯三次曲面的切面(如图 1所示)，因而其结合十分紧密。阀座面具有自适应(中心自动定位重合)和补偿磨损功能。

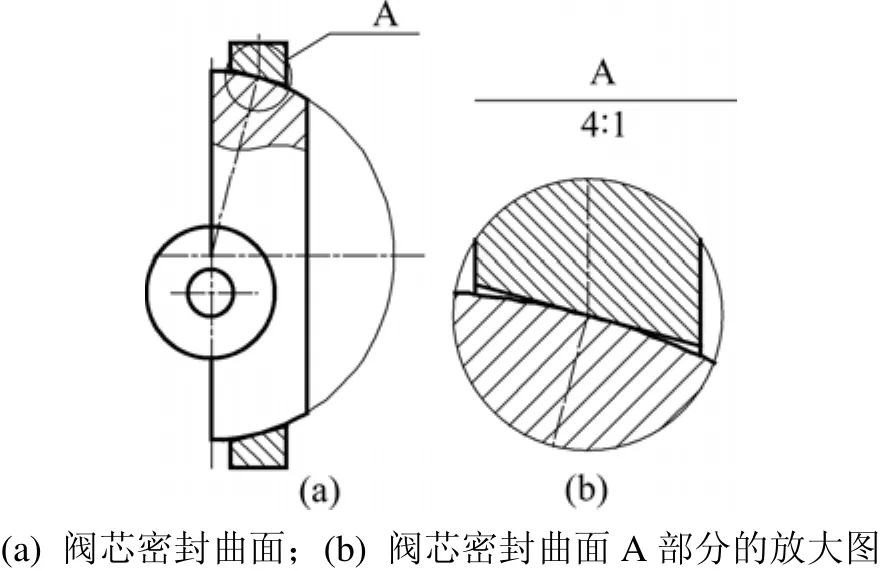
图1 阀芯密封曲面及局部放大图Fig.1 Sealed surface of valve core and its enlarging map

因为转动中心偏离阀芯几何中心，当阀芯打开时，阀芯实体不断向后退、向内缩；当阀芯关闭时，阀芯实体不断向前进、向外胀，其结构与功能相当于半球阀、闸阀、截止阀和蝶阀的综合结构与功能，阀芯实体各不同角度的变化如图2所示。

图2 阀芯实体各不同角度变化图Fig.2 Change process of valve core due to different angle

新型双向流旋球阀在正向压力时密封良好，在反向压力或反向压力大于正向压力时密封也良好。当正向压力作用时，介质压力推动阀板向前移动，阀杆变形，阀板密封面紧贴阀座密封面传递压力，将阀座推向阀体台阶，使之密封良好；当反向压力作用时，介质压力推动阀板向后移动，介质压力同时推动阀座向后移动，阀座密封面紧贴阀板密封面传递压力，将阀座推向阀杆极限变形位置，使其密封良好。正、反向阀座密封示意图如图3所示。

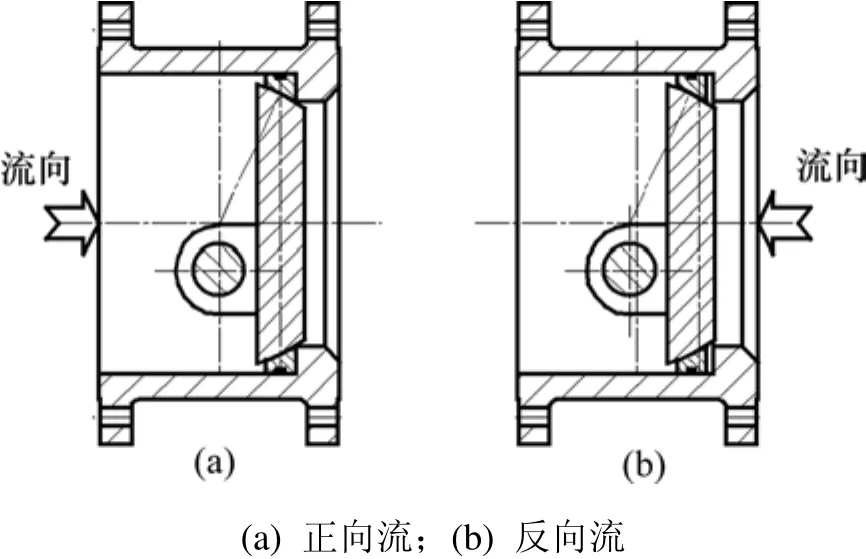
图3 正、反向密封示意图Fig.3 Diagram of double direction sealing

2 新型双向硬密封旋球阀多学科设计优化

2.1 新型双向硬密封旋球阀多学科设计优化思路

多学科设计优化是一种通过充分利用和探索系统中相互作用的协同机制来设计复杂系统和子系统的方法。新型双向硬密封旋球阀多学科设计优化理论方法的主要思想是：在复杂系统设计的整个过程中集成各个学科的知识，应用有效的设计、优化策略和分布式计算机网络系统来进行新型双向硬密封旋球阀设计，通过充分利用各个学科(子系统)之间的相互作用所产生的协同效应，获得新型双向硬密封旋球阀的整体最优设计结果。新型双向硬密封旋球阀分级多学科设计优化结构如图4所示。

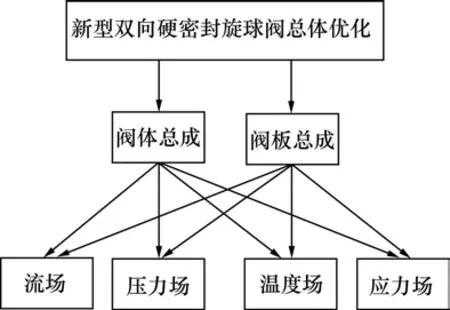
图4 多学科设计优化分级结构Fig.4 Grading structure of multidisciplinary optimization design

按新型双向硬密封旋球阀总体级和部件级(阀体总成和阀板总成)以及零件级(流场、压力场、温度场和应力场等)三级进行多学科优化设计。新型双向硬密封旋球阀总体优化设计的功能是使新型双向硬密封旋球阀的设计成本最低、渗漏量最小、耐久性寿命较长，同时，向各部件分配指标，并以总体与部件指标一致为约束条件；部件级优化设计以与总体级分配指标相差最小为目标函数，在满足部件级的约束条件下，向所属各零件分配指标；零件级优化设计以与部件级分配指标相差最小为目标函数，通过调整零件几何结构尺寸，以满足零件级的各学科约束条件。通过以上 3级优化，使得各零部件与总体间设计达成一致协调(也就是说，各零部件与总体间的复杂耦合关系通过一致性约束解耦)，并找到综合最优的设计方案。在以上过程中，若上一级系统包含过多的下一级系统，则可根据需要在两级系统之间增加1级或多级系统，例如在部件级与零件级间可增加组件级优化。

2.2 新型双向硬密封旋球阀多学科设计优化模型

考虑新型双向硬密封旋球阀的密封性能、流动阻力系数、抗冲击性能、阀板密封面球面度、材料导热系数、质量等因素，根据MDO设计优化思想，得出新型双向硬密封旋球阀优化设计的MDO过程示意图如图5所示。

图5 新型双向硬密封旋球阀MDO过程示意图Fig.5 Chart of MDO process of new type rotating ball valvewith double direction metal sealing

新型双向硬密封旋球阀多学科设计问题是一个数学规划的优化问题，可描述为：

式中：f(X,Y)为目标函数，f(X,Y)=W1f1(X,Y)/f10(X,Y)+W2f2(X,Y)/f20(X,Y)+W3f3(X,Y)/f30(X,Y)+W4f4(X,Y)/f40(X,Y)；f1(X,Y)为密封性能目标函数；f2(X,Y)为质量目标函数；f3(X,Y)为抗冲击性能目标函数；f4(X,Y)为流动阻力系数目标函数；f10(X,Y)，f20(X,Y)，f30(X,Y)和f40(X,Y)分别为未多学科优化前新型双向硬密封旋球阀的泄漏量初始值、质量、阀板变形量和流动阻力系数；W1，W2，W3和W4分别为密封性能目标函数、质量目标函数、抗冲击性能目标函数和流动阻力系数目标函数在总体目标规划中的加权系数，且W1+W2+W3+W4=1；X为设计变量，X=(X1,X2, …,Xm, …,XM)T；Y为状态变量，Y=(Y1,Y2, …,Yk, …,YK)T；gi(X,Y)为约束条件。

新型双向硬密封旋球阀设计优化问题的求解分析过程见图5。在图5中，设计变量X表示新型双向硬密封旋球阀的特征，在设计过程中可被设计者控制相互独立的变量；Z为新型双向硬密封旋球阀固定不变参数；状态变量Y为描述新型双向硬密封旋球阀的性能和特征的参数，也可表示为Y=[y12，y13，y14，y21，y23，y24，y31，y32，y34，y41，y42，y43]，此时Y为所有连接变量组成的向量，且yij(i，j=1，2，3，4；i≠j)为学科之间的耦合变量，或称连接变量，它是子系统i的输出变量，同时是子系统j的输入变量。4个学科分析(Contributing Analysis, CA)之间通过连接变量Y相互交换信息。整体系统的性能(功能函数)gi则是输入参数X和连接变量Y的函数。系统分析可由如下非线性联立方程组表示：

最后对新型双向硬密封旋球阀设计进行系统分析(System Analysis, SA)，从而得到优化设计结果。新型双向硬密封旋球阀MDO求解过程示意图如图6所示。

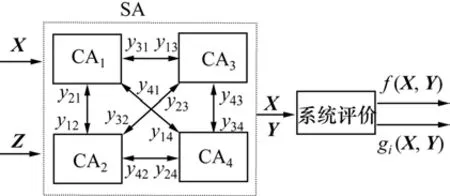
图6 新型双向硬密封旋球阀MDO求解过程示意图Fig.6 Chart of resolution process about MDO of new type rotating ball valve with double direction metal sealing

2.3 自适应混沌优化算法

给定权值W1，W2，W3和W4的取值范围，利用自适应变尺度混沌优化算法[14-15]对式(1)所示的全局优化问题求解，权值W1，W2，W3和W4对应全局优化问题的最小值。

选择式(3)所示的折叠次数无限一维自映射作为产生混沌变量的混沌模型，用K1和K2分别表示粗、细迭代次数。

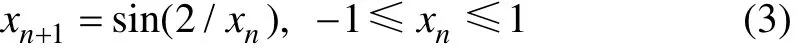
式中：n=0, 1, 2, …,n；xn≠0。混沌优化算法的基本步骤如下。

Step 1 算法初始化。置K1=1，K2=1，并给定2个较大的正整数N1和N2，用随机数产生x0，代入式(3)所示的混沌模型，产生i个混沌变量xi，n+1(i=1，…，M)作为产生搜索迭代用的混沌变量。

Step 2 混沌变量在设计变量区间上的粗略转化。利用式(4)将以上产生的第i个混沌变量由取值范围[-1，1]变换到优化设计变量区间[ai，bi]上的混沌变量。

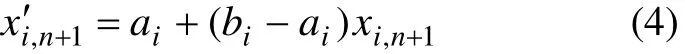
Step 3 用混沌变量进行粗迭代搜索。令xi(K1)=，计算优化解

Step 4 混沌变量搜索区间缩小。设

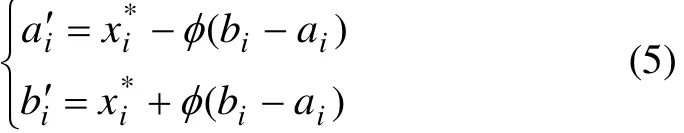
式中：φ为收缩因子，φ∈(0，0.5)。为了保证新范围不至于越界，进行如下处理：若，则若则因此，在新区间[上进行还原处理后由下式确定：

Step 5 混沌变量在设计变量区间上的细转化。

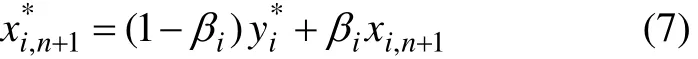
式中：βi为自适应调节系数，0＜βi＜1。

自适应调节系数βi采用如下方法进行自适应确定：

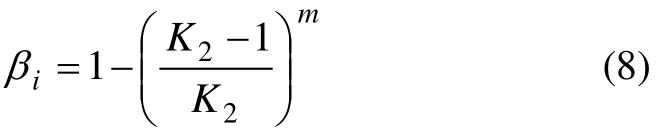
式中：m为整数，根据优化目标函数而定，本文中取m=2。

在细迭代搜索初期，由于(x1，x2，…，xn)变动较大，故需要选用较大的；随着搜索的进行，逐渐接近最优点，故需要选用较小的，以便于在(，…，)所在的较小范围内进行搜索。

Step 6 用混沌变量进行细迭代搜索。令，计算优化解。

(2)若fi(K2)＞，则放弃xi(K2)。当K2≤N2时，进入下一次迭代，K2：=K2+1；当K2＞N2时，结束细迭代。

当得到最优解W1，W2，W3和W4后，将所求得的最优解W1，W2，W3和W4存入内存。

3 新型双向硬密封旋球阀多学科设计优化

新型双向硬密封旋球阀适用介质为清水、污水和油品，其工作压力p不低于0.44 MPa。

3.1 新型双向硬密封旋球阀多目标函数设计

3.1.1 密封性能目标函数

新型双向硬密封旋球阀的渗漏率反映了新型双向硬密封旋球阀的密封性能，其优化变量为(X1,Y1)，其中：X1包括新型双向硬密封旋球阀中心距偏e、阀芯密封圆锥面半径R、阀体半径r1、阀板半径r2、阀杆长度L1、阀板厚度δ1、阀体厚度δ2、密封面宽度b、阀体长度a这9个设计变量参数；Y1包括新型双向硬密封旋球阀启闭时间τ、阀芯密封材料导热系数λ1、阀体密封材料导热系数λ2、阀板导热系数λ3、阀体导热系数λ4、新型双向硬密封旋球阀板所受的应力σ1和新型双向硬密封旋球阀阀体应力σ2、应变ε1和新型双向硬密封旋球阀阀体应变ε2、工作温度θ共10个状态变量参数，故其密封性能目标函数可表示为：

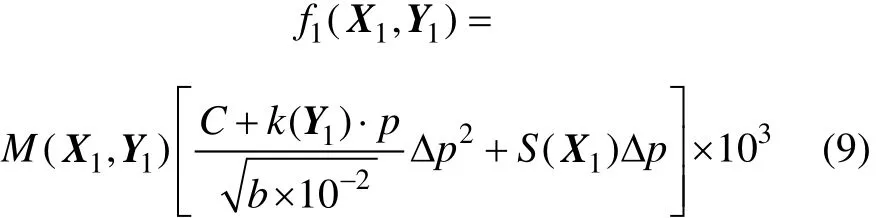
式中：M(X1,Y1)为与材料、密封面加工质量有关的影响系数；C为密封面材料常数；k(Y1)为密封面材料影响系数；S(X1)为与流场、温度场有关的密封面比压修正系数；Δp为介质工作压力与环境压力pb的差值。

3.1.2 质量目标函数

考虑新型双向硬密封旋球阀形状比较复杂，可以分别计算各部件的质量，然后，逐个部件的质量迭加得到整体新型双向硬密封旋球阀的质量，其优化变量为(X2,Y2)，其中：X2包括设计变量参数与X1的相同；Y2不包括任何状态变量参数。新型双向硬密封旋球阀质量目标函数为：

式中：Mi(X2,Y2)为第i个部件的质量函数。

3.1.3 抗冲击性能目标函数

在发生冲击引起模态形变的情况下，新型双向硬密封旋球阀的结构必须有足够的强度才能安全可靠地工作。新型双向硬密封旋球阀结构的位移变形情况反映了旋球阀的抗冲击性能，其优化变量为(X3,Y3)，其中：X3=X2；Y3包括新型双向硬密封旋球阀启闭时间τ、所受应力σ1和σ2、应变ε1和ε2、工作温度θ这6个状态变量参数。其抗冲击性能目标函数可表示为：

式中：K(X3,Y3)为新型双向硬密封旋球阀体结构刚度矩阵；F(X3,Y3)为新型双向硬密封旋球阀体因启闭而引起的等效载荷矩阵；FT(X3,Y3)为等效体积力矩阵，效表面力矩阵Fp(X3,Y3)为等效集中力矩阵，新型双向硬密封旋球阀体单元因启闭而受到的体积力、表面力和集中力；NT(X3,Y3)为位移形状函数矩阵；N1，N2，…，NL为节点1，2，…，L关于(X3, Y3)的形状函数；上标“T”表示矩阵转置；B(X3,Y3)为位移几何矩阵；C(X3,Y3)为结构阻尼矩阵，C(X3,Y3)=分别为新型双向硬密封旋球阀体单元的应力和应变。

3.1.4 流动阻力系数性能目标函数

工质流经新型双向硬密封旋球阀后的流动阻力系数性能优化变量为(X4,Y4)，其中：X4=X1；Y4=Y1。则工质流经新型双向硬密封旋球阀后的流动阻力系数性能目标函数为：

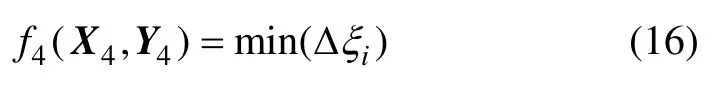
3.2 新型双向硬密封旋球阀设计优化仿真流程

新型双向硬密封旋球阀的参数化建模通过自编程序对自定的、统一格式的参数文件进行操作，分别生成符合流场仿真分析、压力场仿真分析和温度场仿真分析的几何模型文件，并通过优化平台将不同物理场的仿真分析软件和自编程序进行集成，从而实现新型双向硬密封旋球阀的设计优化。不同物理场的耦合关系以及优化仿真集成的流程图如图7所示。

图7 新型双向硬密封旋球阀设计仿真优化流程图Fig.7 Flow chart of design and optimization of new type rotating ball valve with double direction metal sealing

3.3 新型双向硬密封旋球阀多学科设计优化结果

新型双向硬密封旋球阀系统级优化的优化算法为自适应混沌优化算法，其优 化 变 量 为：优化的约束条件包括 16个结构约束、3个几何约束和 4个目标约束，如表1所示。各系统的优化通过VB软件实现双层并行运算。

表2所示为新型双向硬密封旋球阀多学科设计优化前后优化目标的相关参数值。可以看出：新型双向硬密封旋球阀渗漏率η减少 60.0%，质量M减少2.15%，位移变形Δε减少37.6%，流阻系数Δξ减少37.5%。

表1 MDO约束条件Table 1 Constraint conditions of MDO

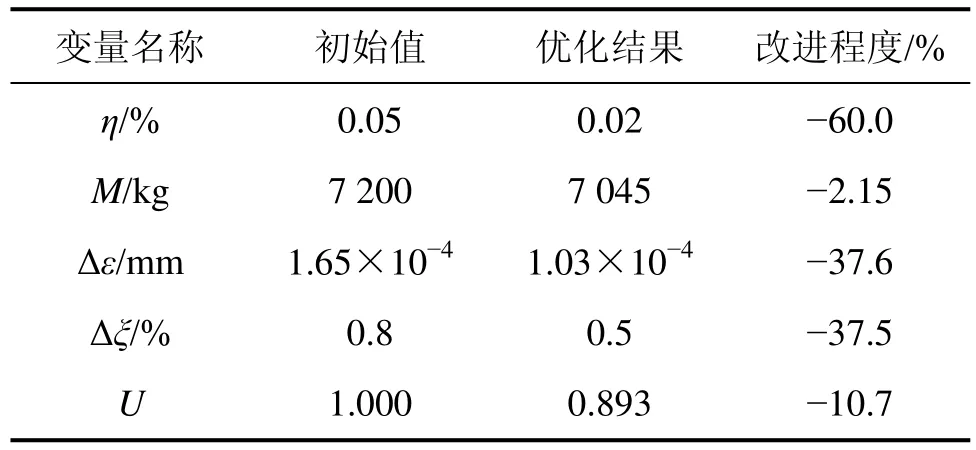
表2 MDO优化目标的相关参数值Table 2 Values of correlative MDO objective parameters

将优化前后新型双向硬密封旋球阀连接在长度为50 m的管段上，分别进行流量调节系数ΔI随阀门开度变化Δn的对比实验，其结果如图8所示。可见：随阀门开度变化 Δn的增大，新型双向硬密封旋球阀的流量调节系数变大，且优化后新型双向硬密封旋球阀的流量调节系数比优化前的流量调节系数大。

图8 新型双向硬密封旋球阀的流量调节性能Fig.8 Flow adjustment efficient of new type rotating ball valve with double direction metal sealing

4 结论

(1)新型双向硬密封旋球阀渗漏率η、质量M、位移最大变形Δε、流阻系数Δξ以及整体性能U均得到了明显改善，其中：新型双向硬密封旋球阀渗漏率η减少60.0%，质量M减少2.15%，位移变形Δε减少37.6%，流阻系数Δξ减少37.5%。

(2)采用多学科设计优化方法来进行新型双向硬密封旋球阀的设计，通过充分考虑各学科之间的耦合效应，既提高了新型双向硬密封旋球阀的传热性能以及抗热冲击性能，又降低了设计成本，减小了质量，因而为新型双向硬密封旋球阀设计提供了一条新的道路。多学科设计优化在新型双向硬密封旋球阀设计中将具有广阔的应用前景。

[1]Chern M J, Wang C C, Ma C H. Performance test and flow visualization of ball valve[J]. Experimental Thermal and Fluid Science, 2007, 31(6): 505-512.

[2]Park J Y, Chung M K. Study on hydrodynamic torque of a butterfly valve[J]. Journal of Fluids Engineering, 2006, 128(1):190-195.

[3]Vetter J, Michler T, Steuernagel H. Hard coatings on thermochemically pretreated soft steels: application potential for ball valves[J]. Surface and Coatings Technology, 1999, 111(2/3):210-219.

[4]SONG Xue-guan, WANG Lin, Seok H B, et al.Multidisciplinary optimization of a butterfly valve[J]. ISA Transactions, 2009, 48(3): 370-377.

[5]Danbon F, Solliec C. Aerodynamic torque of a butterfly valve:Influence of an elbow on the time-mean and instantaneous aerodynamic torque[J]. Journal of Fluids Engineering, 2000,122(2): 337-344.

[6]TIAN Wen-xi, Su G H, WANG Gao-peng, et al. Numerical simulation and optimization on valve-induced water hammer characteristics for parallel pump feedwater system[J]. Annals of Nuclear Energy, 2008, 35(12): 2280-2287.

[7]Atashkari K, Nariman-Zadeh N, Gölcü M, et al. Modelling and multi-objective optimization of a variable valve-timing spark-ignition engine using polynomial neural networks and evolutionary algorithms[J]. Energy Conversion and Management,2007, 48(3): 1029-1041.

[8]Hummer G, Halter G, Grössl M. Calculated and measured flow conductance for butterfly valves[J]. 1990, 41(7/9): 2126-2128.

[9]Jones C, Waldon C, Martin D, et al. Conceptual design of a compact absolute valve for the ITER neutral beam injectors[J].Fusion Engineering and Design, 2009, 84(2/6): 979-984.

[10]Lin J L, Clevenger J M. Modeling and optimizing passive valve designs for the implantable Gold Micro-Shunt used in glaucoma treatment[J]. Computers & Structures, 2009, 87(11/12):664-669.

[11]Harish A, John E R, Evan L P, et al. Uncertainty quantification using evidence theory in multidisciplinary design optimization[J].Reliability Engineering & System Safety, 2004, 85(1/3):281-294.

[12]谢常清, 鄂加强, 彭雨, 等. 制动电阻器多学科设计优化[J].铁道学报, 2008, 30(5): 119-124.XIE Chang-qing, E Jia-qiang, PENG Yu, et al. Multidisciplinary design optimization of electric braking resistor[J]. Journal of the China Railway Society, 2008, 30(5): 119-124.

[13]袁文华, 鄂加强, 龚金科, 等. 自适应粒子群优化的高压共轨燃油喷嘴多学科优化设计[J]. 内燃机工程, 2009(5): 63-67.YUAN Wen-hua, E Jia-qiang, GONG Jin-ke, et al.Multidisciplinary design optimization for fuel nozzle of high pressure common-rail injection system based on self-adaptive particle swarm optimization algorithm[J]. Chinese Internal Combustion Engine Engineering, 2009(5): 63-67.

[14]鄂加强. 铜精炼过程优化建模与智能控制[M]. 长沙: 湖南大学出版社, 2006.E Jia-qiang. Optimal modeling and intelligent control on copper refining process[M]. Changsha: Hunan University Press, 2006.

[15]E Jia-qiang, WANG Chun-hua, WANG Yao-nan, et al. A new adaptive mutative scale chaos optimization algorithm and its application[J]. Control Theory & Applications, 2008, 6(2):141-145.