袋式除尘器流场动态测试及优化

付海明，赵友军

(东华大学 环境科学与工程学院，上海，201620)

袋式除尘器是治理大气污染的高效除尘设备, 对减少气溶胶对大气的污染起重要作用，在化工、冶金、矿山、机械、水泥、粮食、制药、轻工等行业已得到广泛应用，它主要用来捕集细小、干燥的非纤维性粉尘，袋式除尘器的粉尘排放浓度可达到 10 mg/m3以下。降低气流流通阻力及延长滤袋的使用寿命，减少振动和噪音，是袋式除尘器需要解决的问题。袋式除尘器破损滤袋大部分集中在除尘器下游，这与箱体内部气流状况密切相关。合理调整气流分布可以降低运行阻力，延长滤袋的使用寿命，减少振动和噪音。许多学者对袋式除尘器气流分布进行了模拟研究[1-4]，其中：桑亮等[1]在除尘器内部没有挂装滤袋况下，对布袋除尘器内部未布置导流板和加有导流板的内部流场分布进行测试，发现安装导流板的气流均布性与没有气流均布装置时相比有很大提高，但其忽略了内部滤袋的影响，试验测试结果不能完全反映袋式除尘器内部流场的实际分布。在此，本文作者对袋式除尘器内部流场的分布进行实验测试，将实验测试结果与模拟计算结果进行对比，确定必要的边界条件，建立CFD模拟研究模型，以利用数值模拟替代部分实验[5-6]对袋式除尘器内部气流组织分布进行模拟计算，分析流场特性，以节省人力和物力，优化设计袋式除尘器。

1 模型建立及数值计算方法

1.1 模型的建立

对除尘器整体进行模拟。由于袋式除尘器的内部结构比较复杂，为了利于模型建立和方便计算，进行以下假设和简化：

(1)本文试验测试研究是在常温下于室内进行，颗粒和气体的混合物看作是一种均匀介质，它们之间没有相对滑移；在进行模拟时，可以把这种稀相气固两相流近似简化成具有平均流体特性的单相流[7-8]。

(2)只考虑除尘器入口至袋式除尘器的花板处为止，也不计出口净气箱、文丘里(对于脉冲方式的袋式除尘器)等部件的影响。

(3)除尘器入口的气流速度分布实际上并不均匀[9-11]，在模拟时，假设入口处气流速度分布均匀。

1.2 数值计算方法

通过分析各湍流模型的优缺点，确定采用 RNGk-ε模型进行模拟分析(其中：RNG即Renormalization group；k为湍动能；ε为耗散率)。模拟计算时，选择速度入口边界条件。应注意的是：只有垂直于控制体表面的流动分量才对流入质量流速有贡献。出口边界条件如下：选取压力出口边界条件，壁面为静止壁面，固体壁面边界无滑移，在壁面处具有零梯度，在壁面上采用标准壁面函数。

在设置多孔介质边界条件时，不可简单地将其设成跳跃边界条件。虽然将多孔介质简化成一维模型时有利于收敛，但与实际的流场相差较大，宜设置为多孔介质边界条件。本文模拟采用国产729滤料，其孔隙率为0.4，压力边界条件参数由试验测试确定，通过实验得出多孔介质压力与过滤速度的关系为：

式中：Δp为过滤介质压力损失(Pa)；v为过滤速度(m/s)。

2 评价流场分布的基本参数

2.1 不均匀度

袋式除尘器内部断面各点的气流速度不可能完全相同，本文采用美国 RMS标准的判定方法，即相对均方根法。相对均方差公式为[7]：

式中：vi为测点上的流度(m/s)；为断面平均流速(m/s)；n为断面上的测点数。

RMS标准的特点是对速度场的不均匀度反映比较灵敏，其均方根越大，不均匀度便越高。过滤速度v为1.30 m/min以及0.80 m/min时的气流不均匀度见图1。

图1 气流不均匀度对比图Fig.1 Contrast of uneven flow

由图1可知：由于进风口开口面积较小，气体进入除尘器下箱体后形成明显的射流作用，因此，气流分布很不均匀，在中箱体的下部其气流间隙速度过大，超过了设计值，特别是后壁面的速度过大，造成局部的过滤速度太大，以至于损坏滤袋，并且降低其过滤效率。

2.2 流量分配系数

滤袋的流量分配系数表示每个滤袋实际处理气体流量与平均处理气体流量的比值，记作Kqi，即

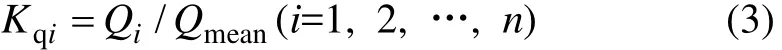
式中：Qi为单个滤袋的实际处理气体量(m3/s)；Qmean为单个滤袋的平均处理气体流量(m3/s)。

2.3 最大流量不均幅值

最大流量不均幅值是指最大流量分配系数和最小流量分配系数的差值，计作ΔKqi。

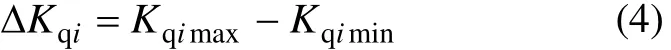
或

式中：Kqimax为单个滤袋的最大流量分配系数；Kqimin为单个滤袋最小流量分配系数；Q+为单个滤袋处理气体量的最大正偏差；Q-为单个滤袋处理气体量的最大负偏差。

当气体流量分配不均匀时，Kqi在1.0附近波动，且ΔKqi≠0，其值越大，表明气流均匀性越差，反之，说明比较均匀。当气体流量分配绝对均匀时，Kqi=1.0，ΔKqi=0。由于绝对均匀是理想状况，所以规定：只要气流分配达到一定程度时便可以认为气体流量分配均匀。一般地，当处理风量的相对偏差不大于15%时，便可以认为气体流量分配基本均匀。

2.4 综合流量不均幅值

综合流量不均幅值是指所有滤袋的流量分配系数与理想状态下的绝对均匀系数1.0之差的绝对值的平均值。这个参数综合考虑了各个滤袋的流量偏差，评价比较全面，计作即

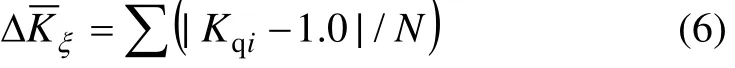
式中：N为模型中滤袋的总个数。

3 流场分布的计算机模拟

实验测点平面及模拟研究模型如图2所示。模型的进风口在中箱体下部靠近滤袋底部位置，中箱体高度为1.2 m，截面面积(长×宽)为600 mm×600 mm，下箱体上部进进为正方形，下部出口为圆型，简称天方地圆型，高为200 mm，入口直径为120 mm，滤袋长度L=1 m，滤袋直径为 100 mm，滤袋长×宽为140 mm×140 mm，共16个滤袋。此模型设入口速度为6.09 m/s，过滤速度为0.80 m/min。

Z=250 mm及Y=230 mm截面速度模拟矢量图如图3和图4所示。由图3可知：气流在与后壁面碰撞后，气流沿着壁面形成回流，而回流是造成侧壁面速度过大的主要原因。由于袋式除尘器的中箱体前壁面与滤袋之间存在较大空间，而气流总是向着阻力小的位置流动，因此，前壁面气流有爬升现象。图4有效地再现了这种现象。同时，从图4中的放大图可以看到气流进入滤袋的方向，由于存在滤袋，气流通过滤袋时的过滤速度明显比滤袋中心速度以及气流间隙速度小很多。从图3可以看出：在靠近除尘器气流进口的位置其气流比较紊乱，气流分布很不均匀，气流间歇速度过大，同时，滤袋表面过滤速度也超过设计值，这样对底部滤袋造成很大的冲刷作用。此外，由于在除尘器中被过滤的颗粒物向下运动，当颗粒物下降到气流射流处时，又会被射流重新带回到中箱体，加大了滤袋的负荷，从而损坏滤袋，缩短其使用寿命。

不同滤袋中心轴向气流速度模拟结果如图 5所示。由图5可知：气流速度呈波形变化；当与入口听垂直距离大于0.85 m时，轴向气流速度基本上随着离入口距离的增大而增大。由于滤袋出口面积相同，因此，出口速度差别不大，在离中箱体上壁大约300 mm时，8个滤袋的中心轴向气流速度变化基本一致。

气流分布情况见表1。可见：1号、2号和5号滤袋的出口流量偏大，而4号和8号滤袋的出口流量偏小；气流分布系数Kqi的最大和最小值分别出现在 1号滤袋和 8号滤袋上；最大流量不均幅值ΔKqi达到0.226，综合流量不均幅值为0.073，流量分配不均匀；气流分布不均匀，在滤袋底端，不仅气流间歇速度过大，超过了设计值，而且当气流的含尘浓度也很高时，对滤袋会造成严重冲刷作用，这样必然会降低滤袋的使用寿命。

图2 实验测点平面及模拟研究模型图Fig.2 Diagram of experiment measuring plot and simulation model

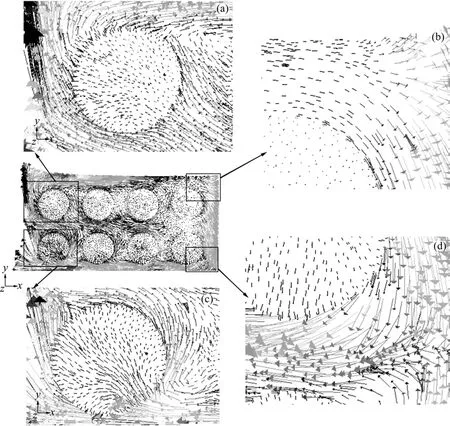
图3 Z=250 mm的截面速度矢量图Fig.3 Diagrams of velocity vector at Z=250 mm

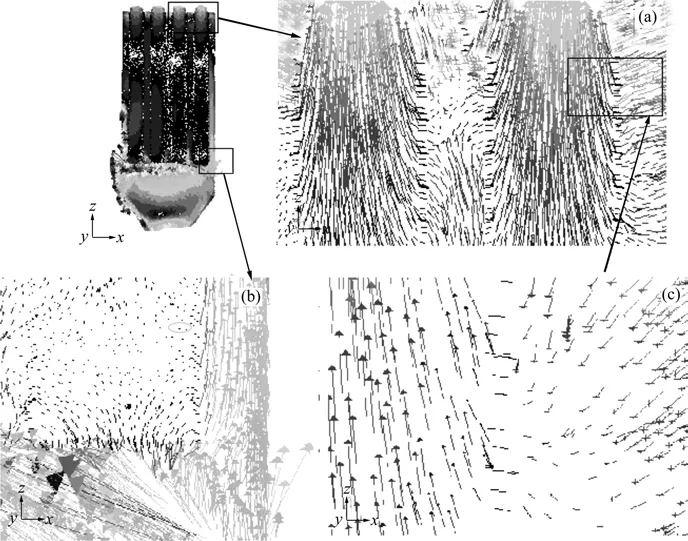
图4 Y=230 mm的截面速度矢量图Fig.4 Diagrams of velocity vector at Y=230 mm

图5 不同滤袋中心轴向气流速度Fig.5 Flow velocity of central axis in deferential filter bag

4 试验测试值与模拟值对比

选取具有代表性的截面4，6，8和10这4个截面共128点的测定速度和模拟速度进行对比分析，部分测点试验测定速度和模拟速度对比结果如图6所示。图中袋式除尘器入口过滤速度均为0.80 m/min；实验测点气流速度呈布袋四角分布，模拟速度计算值呈布袋圆周围气流分布。由图6可知：实验测试速度与模拟速度基本相同。

试验测试和模拟的相对误差小于 17.5%。误差主要由测试仪器的精度及以下几个方面引起：

(1)试验模型的工艺影响。在建立试验台时，由于实际操作情况限制，不可能建立理论上的完美模型，如除尘器外壳的不平整性、滤袋安装位置的偏差等均会产生误差。

(2)测试工况的影响。本试验是在忽略一系列因素下进行的，如：忽略了室内温度变化的影响，气体密度变化的影响，风机特性、设备漏风以及安全质量的影响等。这些因素将导致试验结果产生一定误差。

(3)测试时的误差影响。在实际测试时，由于除尘器壁面上打有320个测孔，测孔的存在对除尘器的流场有一定的影响，进而影响速度测试值的准确性；测点位置与模拟计算点位置存在一定偏差。另外，在实际测试时，探针的稍微晃动会使速度测试值产生跳跃。

(4)模型简化的影响。在建立模型时，只考虑袋室入口至袋式除尘器的花板处为止，不计出口净气箱等部件的影响。

(5)边界条件设定的影响。在边界条件的设定中，对流场模拟影响最大的是滤袋的边界条件设定。本文将滤袋设定为多孔介质，并认为是各向同性材料[12-13]。因此，模拟的流场与实际工况流场存在一定差距。

综上所述，气流速度试验测试值和模拟值存在相对误差，但小于17.5%，因此，采用CFD进行袋式除尘器流场的模拟对实际工程应用有一定的参考价值。由流场测试结果与模拟结果可知：流场的不均匀性主要是入口风速过高和袋室结构不合理所致。由于入口的高速射流效应，使得气流分配不均匀现象严重，其部分间隙速度大于设计参考限值，而且滤袋底部气流速度过大，容易使滤袋提前破损。

表1 流量分配系数KqiTable 1 Parameters of flow volumes Kqi

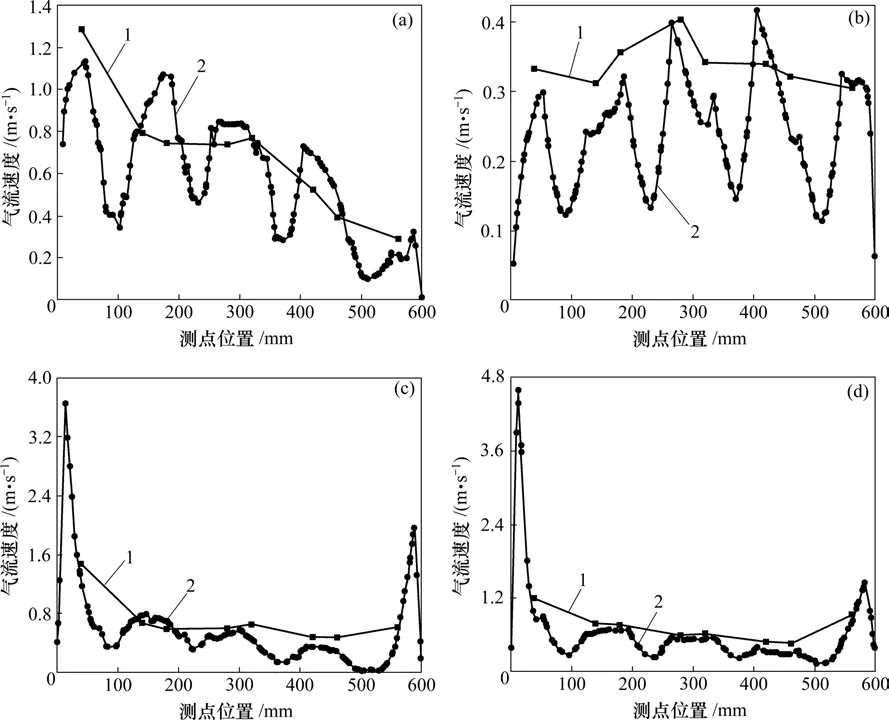
图6 试验测点与模拟对比图Fig.6 Contrast diagram of experimental result and simulation result

5 袋式除尘器流场模拟优化设计

针对不同的进风方式、袋室结构建立2种不同的模型；通过对这些模型进行模拟与分析，了解不同的进风方式对袋式除尘器内部气流组织的影响规律，比较2种模型的优缺点，以便优化袋式除尘器结构，为实际应用提供更合理的袋式除尘器结构参数。

5.1 下箱体安有钝体的进风模型

下进风式袋式除尘器不需要上进风式结构中复杂的均流板，具有结构简单的优点，但是，其气流分布不均匀[6-14]，特别是由于受设备安装空间限制或者没有充分考虑流动均匀性要求而设计出的某些结构中，流动不均匀问题可能十分严重，使分离效率降低，运行阻力增加，甚至加速滤袋破坏，形成气流短路。Croom 等[7-15]提出了一些改进措施，有一定的借鉴意义。

本文提出2项改进措施：扩大进风管面积；在袋室下箱体中布置钝体。前者是为了降低入射气流速度，后者在于使气流形成均匀的纵掠滤袋流动。经过多次数值模拟，确定如图7所示的袋室结构改进方案，其流场分布均匀性分析结果如表2所示。由表2可知：靠近壁面的1，4，5和8号滤袋出口流量分配系数偏大，而中间滤袋的出口流量分配系数偏小；最大流量不均幅值ΔKqi为 0.029，综合流量不均幅值为0.014，流量分配基本均匀。流场分布均匀是由于入口面积扩大以及存在钝体，入口气流速度降低，气流在进入除尘器下箱体后已没有明显的射流存在，除尘器中气流分布基本均匀，间歇速度小于设计值，不会对滤袋起冲刷作用。

5.2 装有气流均布板的单入口侧进风模型

为了使气流分布更加均匀化，也可采用侧进风入口，并加有气流均布板的流场改进方案，改进模型如图8所示，气流均布板具体设计参数如图9所示。当含尘气体从进风口进入中箱体后先碰上进风口气流均布板，由于惯性作用，使气体粗颗粒粉尘直接进入灰斗，起到预收尘作用；此外，在气流均布板的截流作用下气体被分散流动，从每个滤袋外侧进入滤袋内，在滤袋的筛分、拦截、冲击、扩散和静电吸引等作用下，粉尘贴附于滤布缝隙间，因而使粉尘从烟气中分离出来，清洁的气体经抽风机、抽风管排入大气。装有气流均布板的单入口侧进风的流场分布均匀性分析结果如表3所示。由表3可知：除7号和8号滤袋出口流量分配系数稍小外，其余流量分配系数基本相等，最大流量不均幅值ΔKqi为 0.083，综合流量不均幅值为 0.019，流量分配均匀。其原因是含尘气体从进风口进入中箱体后先碰上进风口气流均布板，由于惯性作用，使气体粗颗粒粉尘直接进入灰斗，起到预收尘作用；此外，在气流均布板的截流作用下气体被分散流动，其速度进一步降低。因此，建议在侧进风的除尘器入口处加装气流均布板装置，使气流在进入除尘器后速度得到控制，不至于出现速度过大的现象。

图7 加有钝体的袋式除尘器半图及袋室结构剖视图(单位：mm)Fig.7 Diagram of structure of bag filter with bluntness body

表2 改进模型1流场的流量分配系数KqiTable 2 Flow distribute parameter Kqi of improvement model 1

表3 改进模型2流场的流量分配系数KqiTable 3 Flow distribute parameter of Kqi improvement model 2

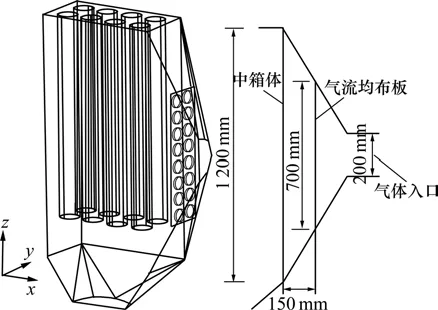
图8 加有气流均布板的单入口袋式除尘器Fig.8 Single entrance bag filter with even current board

图9 气流均布板简图Fig.9 Even current board

6 结论

(1)除尘器内部流场气流分布很不均匀。在滤袋底端，气流速度超过了设计值，对滤袋造成严重冲刷，降低滤袋的使用寿命。

(2)对袋式除尘器流场进行CFD模拟计算，将流场速度分布模拟计算结果与实验测试结构对比，试验测试值与模拟值相对误差小于17.5%。

(3)流场的不均匀性主要是入口风速过高和袋室结构不合理所致。本文提出的扩大进风管面积和在袋室下箱体中布置钝体这2种流场改进方案，使综合流量不均匀幅值由原来的0.073降低到0.019，最小降低幅度为74%。用这2种方案均可以使袋式除尘器中气流分布基本均匀，气流流通阻力降低。

[1] 桑亮, 杨景玲, 孙体昌. 脉冲喷吹袋式除尘器气流分布模拟试验研究[J]. 能源与环境, 2006(2): 43-48.SANG Liang, YANG Jin-ling, SUN Ti-chang. Pulse jet bag filter simulation study of air distribution[J]. Energy and Environment,2006(2): 43-48.

[2] 高晖, 郭烈锦. 除尘器袋室结构改进及内部气固两相流动特征分析[J]. 西安交通大学学报, 2000, 34(5): 50-54.GAO Hui, GUO Lie-jin. Dust collector bag room and internal structure to improve the flow characteristics of gas-particle analysis[J]. Journal of Xi’an Jiaotong University, 2000, 34(5):50-54.

[3] 党小庆, 袁胜利, 姚群, 等. 直通式袋式除尘器流量分配计算流体动力学方法研究[J]. 热力发电, 2005(9): 29-32.DANG Xiao-qing, YUAN Sheng-li, YAO Qun, et al. A straight-through bag filter flow distribution method of computational fluid dynamics[J]. Thermal Power Generation,2005(9): 29-32.

[4] 高晖, 郭烈锦. 下进风袋式除尘器内部气固两相流动数值模拟[J]. 化学工程, 2001, 29(5): 35-38.GAO Hui, GUO Lie-jin. Under the inlet bag-house Numerical simulation of internal gas-solid flows[J]. Chemical Engineering,2001, 29(5): 35-38.

[5] 刘云卿, 龚金科, 鄂加强. 过滤体结构对柴油机微粒捕集器加热再生过程影响的数值研究[J]. 中南大学学报:自然科学版,2007, 38(2): 314-319.LIU Yun-qing, GONG Jin-ke, E Jia-qiang. Numerical study of effect of monolith structure on pyrogenation regeneration process in diesel particulate filter[J]. Journal of Central South University: Science and Technology, 2007, 38(2): 314-319.

[6] LIU Dai-fei, DING Feng-qi, ZHANG Hong-liang, et al.Numerical simulation of high temperature air combustion in aluminum hydroxide gas suspension calcinations[J]. Trans Nonferrous Met Soc China, 2009, 19(1): 259-266.

[7] Croom M L. New developments in filter dust collection[J].Chemical Engineering,1996, 103(8): 80-84.

[8] Simmons W S, Rinne S P, Tesche N S, et al. Toxicology of fossil fuel combustion products, Vols.1 and 2[R]. Palo Alto, EPRI EA-3920, EPRI, 1985.

[9] Jr Ferris B G. Health effects of exposure to low levels of regulated air pollutants: A critical review[J]. J Air Pollut Control Assoc, 1978, 28(5): 482-497.

[10] Wan de Haar T O. Power pulse tank system offers improved fitter cloth cleaning[J]. Filtration & Separation, 2001, 38(10):36-39.

[11] Croom M L. Effective selection of filter dust collectors[J].Chemical Engineering, 1993, 100(7): 86-91.

[12] Versteeg H K, Malalasekera W. An introduction to computational fluid dynamics: The finite volume method[M]. New York: Wiley,1995.

[13] Subrenat A, Bellettre J, Cloirec P L. 3-D numerical simulations of flows in a cylindrical pleated filter packed with activated carbon cloth[J]. Chemical Engineering Science, 2003, 58(22):4965-4973.

[14] Baleo J N, Subrenat A, Cloirec P L. Numerical simulation of flows in air treatment devices using activated carbon cloths filters[J]. Chemical Engineering Science, 2000, 55(10):1807-1816.

[15] Croom M L. New developments in filter dust collection[J].Chemical Engineering, 1996, 103(8): 80-84.