动三轴试验在武汉地铁二号线勘察中的应用与分析

王瑞芳，张三定，龚福洪，李勇泉

(1.武汉科技大学 城建学院 土木系，武汉 430070;2.长江岩土工程总公司，武汉 430010;3.武汉大学 土木建筑工程学院，武汉 430072)

1 工程概况

武汉市轨道交通二号线一期工程从常青花园北起，穿过张公堤，经汉口火车站，沿青年路、解放大道、江汉路，在武汉关穿长江，至武昌四棉，沿和平大道、中山路，穿小龟山到洪山广场和中南路，沿武珞路、卓豹路到终点鲁巷广场，正线全长约27 km。全线除车辆段及相应出入线为地面线外，其余段均为地下隧道。在循礼门站场地分布饱和砂土和粉土，根据要求对本区段地基土进行液化判别。

2 试样情况

2.1 取样情况

试样取自武汉轨道交通2号线一期工程Ⅲ标段工程场地，共六组，具体描述如下:①D-1:取样深度17.2～17.4 m，灰色粉质黏土，软塑态，试样天然重度为19.05 kN/m3;②D-2:取样深度19.2～20.1 m，灰色粉质细砂，试样天然重度为21.16 kN/m3;③D-3:取样深度22.00～22.2 m，灰色粉质细砂，其试样天然重度为21.56 kN/m3;④D-4:取样深度28.2～28.4 m，黄褐色粉质细砂，试样天然重度为19.63 kN/m3;⑤D-5:取样深度31.4～31.6 m，黄褐色粉质细砂，试样天然重度为19.45 kN/m3;⑥D-6:取样深度37.6～37.8 m，灰色粉质黏土，软塑态，有粉细砂夹层，试样天然重度为19.56 kN/m3。

2.2 试验内容和要求

进行动模量和阻尼比试验，求取土在动荷载作用下的动应变、动模量和阻尼比，最大动模量和最大阻尼比，以及试验参数 a、b。试验固结压力根据取样深度确定，固结应力比KC=1.0;振动频率f=1 Hz;振动波型为正弦波。

2.3 试验设备

试验仪器采用日本诚研舍株式会社制造的DTC-306型电液伺服控制振动三轴仪，如图1所示。其主要技术参数如下:频率为0.01～100.00 Hz，最大轴向荷载5 000 kN，最大围压1 MPa，控制方式有应力控制式或应变控制式，采用正弦波形，相位差为0°～360°，可以单独或同时在轴向和侧向施加动荷载。试验尺寸为 φ 39.1 mm，高 h为 80 mm。

图1 电液伺服控制振动三轴仪

图2 滞回圈

2.4 试验过程

1)试样制备:将试样制备成直径50 mm，高100 mm的圆柱状试样。

2)试样饱和:对黏土和粉质黏土试样采用真空抽气饱和方法，测定试样的饱和度。

3)试样固结:根据试样的取样深度，施加有效固结压力，进行固结，黏土和粉质黏土试样固结完成的时间为8～10 h。

4)施加轴向动荷载:按由小到大的顺序逐级施加动荷载，直到试样破坏，每级动荷载下振动10个循环，采用X-Y记录仪记录每级动荷载下的应力应变滞回圈。每级加荷后，下级加荷前消除试样内的残余孔隙水压力增量。

3 试验成果

3.1 阻尼比的计算

将土当作黏弹性体时，一般用重复加载卸载滞回曲线法来确定土的阻尼比。用动三轴试验的资料在一个周期内整理出轴向动应力与动应变的关系曲线，称为滞回圈。对选取的滞回曲线拟合为椭圆，则椭圆长轴的斜率为动弹性模量，长轴与椭圆交点坐标为动应力幅值和动应变幅值，如图2所示。阻尼比计算方法如式(1)

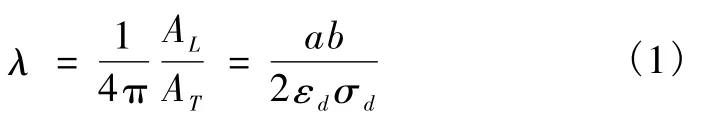
AL为滞回圈面积，表示加载与卸载损失的能量;AT为滞回圈顶点至原点连线与横轴形成的直角三角形的面积，表示加载或卸载的应变能;a、b分别为椭圆长轴、短轴长度;εd、σd分别为轴向动应变和动应力。

3.2 动应力与动应变关系分析

图3为动应力σd和动应变εd在不同围压作用下的关系。由图3可知，动强度随围压呈非线性增长，增长速率逐渐减缓;小应变情况下，应力随应变的增长较快，动弹性模量Ed计算公式为Ed=σd/εd，Ed变化较大;随着应变的增长，应力与应变关系趋于稳定，即动弹性模量不再增长。

图3 σd—εd关系曲线

3.3 不同围压下γ—G/Gmax的关系

土的动剪切模量的退化，通常以动剪切模量比G/Gmax与动剪应变幅值 γ之间的关系表示，即 G/Gmax=1/(1+ γ/γγ)，γγ为参考剪应变。

图4 γ—G/Gmax关系曲线

从图4可以看出，随着剪应变γ的增大，G/Gmax逐渐减小。当剪应变γ<0.025，G/Gmax降低幅值很快;当γ≥0.025时，G/Gmax逐渐趋于稳定。在相同剪应变下，随着围压的增大，相应的G/Gmax也大些。

γ—G/Gmax非线性关系曲线对土层地震反应分析的结果影响显著，对于小震，地表加速度反应谱中特征周期的影响比对地震影响系数的影响更敏感一些;对于大震，则地表加速度反应谱中地震影响系数的影响比对特征周期的影响更敏感一些。

3.4 阻尼比λ与动应变εd的关系曲线

动应变对阻尼比λ有显著的影响，λ随着动应变的增大而增大。这是因为动应变越大，土体内阻消耗能量越多，因此阻尼比会变大。但阻尼比随动应变的增幅却是不同的。在小应变幅下，λ—εd曲线较陡，λ增长较快;而随着动应变的增大，λ增长趋于平缓，逐渐趋于一个定值λmax。

同时，在相同应变下，阻尼比 λ随着固结压力 σ3围压的增大而有所减小，但减小幅度不均。图5中三条曲线所示，在试验开始阶段，在相同应变下，λ在不同围压下取值相差不大，尤其是 σ3=250 kPa，300 kPa，350 kPa的曲线几乎重合。但是随着应变的发展，σ3对阻尼比的λ影响就逐渐明显起来，相同应变条件下，低围压情况下的λ明显大于高围压情况下的λ。

图5 λ—εd关系曲线

3.5 阻尼比λ与剪应变γ的关系曲线

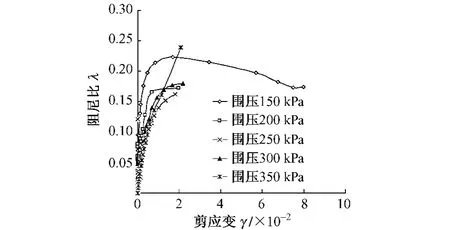
图6 λ—γ关系曲线

剪应变幅值对动剪切模量比和阻尼比值有很大的影响。如图6所示，随剪应变幅值的增大，动剪切模量比减小，阻尼比增大。在相同应变下，阻尼比λ随着固结压力σ3围压的增大而有所减小，但减小幅度不均。当围压为150 kPa时，阻尼比在0.18～0.23范围内变动，当γ≤0.02，阻尼比增大，γ>0.02，阻尼比逐渐减小;随着围压的增大，阻尼比逐渐减小。

4 场地液化判别

场地分布饱和砂土和粉土，根据要求对本区段地基土进行液化判别。由于场地中粉土的黏粒含量为13.2%～27.3%，符合在地震烈度7度情况下黏粒含量不小于10%的条件，可判为不液化土。

5 结论

本文通过室内动三轴试验，分析围压土的动力特性的影响，得到了一些结论:

1)围压对粉砂、粉土的动强度有明显的影响，粉砂、粉土的动强度、动弹性模量随着围压的增大都有明显的提高;随着围压的增大，相应的最大动应变减小。

2)随着剪应变γ的增大，G/Gmax逐渐减小，当剪应变 γ<0.025，G/Gmax降低幅值很快;当γ≥0.025时，G/Gmax逐渐趋于稳定。

3)动应变对阻尼比λ有显著的影响，λ随着动应变的增大而增大。在小应变幅下，λ—εd曲线较陡，λ增长较快;而随着动应变的增大，λ增长趋于平缓，逐渐趋于一个定值λmax。

4)随剪应变幅值的增大，动剪切模量比减小，阻尼比增大。在相同应变下，阻尼比λ随着固结压力σ3围压的增大而有所减小，但减小幅度不均。

5)在地震烈度7度情况下，场地中饱和砂土和粉土的黏粒含量超过10%，可定为非液化土。

[1] 谢定义.土动力学［M］.成都:西南交通大学出版社，1988.[2] 王闻韶.土的动力强度和液化特性［M］.北京:中国电力出版社，1997.

[3] 何昌荣.动模量和阻尼的动三轴试验研究［J］.岩土工程学报，1997，19(2):39-48.

[4] 赵红芬，何昌荣，王莉娜.动模量阻尼的动三轴试验研究［J］.路基工程，2009(4):158-160.

[5] 张启辉，孙红，王挥，等.上海软土的动三轴试验和非线性损伤模型［J］. 土工基础，2007，21(4):54-57.

[6] 孙静.岩土动剪切模量阻尼试验及应用研究［D］.北京:中国地震局工程力学研究所，2004.

[7] 孙静，袁晓铭，孙锐.土动剪切模量和阻尼比的推荐值和规范值的合理性比较［J］.地震工程与工程振动，2004，24(2):125-133.

[8] 张誉，王汝恒，贾彬.砂卵石土在动荷载作用下的阻尼比研究［J］.工业建筑，2008，38(4):59-62.