小波包能量谱在滚动轴承故障诊断中的应用
2010-07-25王冬云张文志张建刚
王冬云,张文志,张建刚
(1.燕山大学 轧机研究所,河北 秦皇岛 066004;2.秦皇岛职业技术学院,河北 秦皇岛 066100;3.秦皇岛首钢板材有限公司,河北 秦皇岛 066003)
滚动轴承是机械中最常用的部件之一,其运行情况直接影响到主机的机能。振动作为一种信息因子直接预示着运行状态的正常与否。因而对轴承进行振动监测和诊断是可行的,且必将获得较大的经济效益[1]。
当轴承系统发生故障时,振动信号能量的空间分布与正常系统的振动信号相比会发生相应的变化,即振动信号的能量改变包含着丰富的故障特征信息。小波变换的时域和频域的局部化和可变分辨率的特点使得用它分析瞬变信号具有比传统Fourier分析更为显著的优点[2]。目前,小波变换法被广泛应用于轴承故障诊断系统。该方法的主要缺点是对高频部分的频率分辨率相对较低。而轴承出现故障时,高频带分解却又是至关重要的,因而往往难以得到满意的识别效果。
小波包分析能为信号提供一种更精细的分析方法。其对信号的低频和高频部分都进行分解,可对非平稳和突变信号进行精确的特征提取,更有效地反映信号的时频特征。文献[3-4]将小波包分析方法应用于轴承故障诊断,并建立了人工神经网络诊断模型,展示了小波包分析在轴承故障特征提取的有效性。但轴承运行状态从正常到异常是一个渐变过程,所表现出来的征兆在很多情况下具有模糊性,神经网络模型不能够对其特征信号的模糊特性充分体现。而以模糊数学为理论基础的聚类分析方法为解决这类模糊性问题提供了新的途径[5]。鉴于此,采用基于小波包能量谱的滚动轴承故障特征提取方法,并提出应用模糊聚类法进行诊断。试验证明,此方法能有效地对轴承进行状态监测与故障诊断。
1 小波包能量谱特征量提取
1.1 小波包分解
3层小波包分解树如图1所示,其中,S为原始信号,H和G分别为正交共轭低通滤波器和高通滤波器,通过小波包分解后可以把信号无泄漏、不重叠地分解到相邻的独立频段上。分解后得到第3层8个频带的小波包分解系数,每个频带的频率范围为:[(n-1)2-j-1fs,n2-j-1fs],n=1,2,3,...8,其中fs为采样频率。

图1 小波包分解结构图
可见,小波包分解[6]可以以更高的分辨率展示信号在不同频段的时域信息,为准确提取信号特征提供了强有力的工具。
1.2 能量谱特征量提取
由于轴承出现故障时会对各频带内信号能量有较大的影响,根据不同频段内能量的分布情况可以诊断出故障的类型。从小波包分解结果中提取频段能量作为信号特征可有效反映轴承运行状态的变化。这种以能量方式表示的小波包分解结果称为小波包能量谱。因此,在小波包能量谱中,可以选取各频带内信号的平方和作为能量的标志,为进一步的故障识别提供了诊断的前提条件。
以3层小波包分解为例,说明故障信号小波包能量谱特征量提取方法[7]:
(1)首先对振动能量信号进行3层小波包分解,从而得到第3层从低频到高频8个子频带的小波包分解系数

(4)构造特征向量。由于系统出现故障时会对各频带内信号能量有较大的影响,因此,以能量为元素可以构造一个特征向量。特征向量T构造如下:

根据各频带能量所占比重的变化即可实现对轴承运行状态的监测。
2 试验及数据处理分析
2.1 试验装置
为了验证提出的诊断方法的有效性,进行了轴承故障诊断试验研究。根据故障诊断理论模型,建立了由直流电动机、齿轮箱、采集系统、信号分析系统组成的试验系统见图2。通过该试验平台,可以模拟齿轮箱轴承的各种故障状态,包括轴承的内圈、外圈故障,并采集故障信号。用于试验的轴承型号为6406,通过安装在齿轮减速器中轴承座外侧的加速度传感器,测取轴承处于不同故障时的加速度信号。
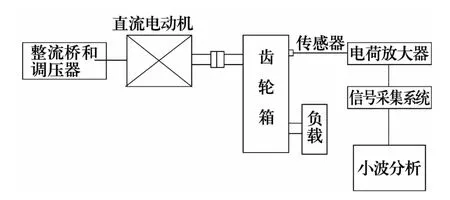
图2 故障诊断试验装置
2.2 试验步骤及结果
首先,用电火花蚀刻技术在一套轴承的内滚道和另一套轴承的外滚道上分别加工直径为4 mm的孔,产生类似凹痕的表面损伤来模拟轴承内圈故障与外圈故障。启动试验平台,轴承内圈转速为900 r/min,而外圈保持静止。采样频率为fs=5 000 Hz,采样时间为0.248 s。正常工况与故障轴承的时域波形信号如图3所示。

图3 轴承振动信号时域波形
2.3 信号处理

根据小波包能量谱特征量提取方法,计算出各个频段的能量,并以此作为特征参数,依次排列做为特征向量。在此分别提取正常工况、外圈故障和内圈故障3种运行状态的特征向量各3组,作为诊断的标准样本,如表2所示。

表1 3层小波包分解后节点对应的频率范围

表2 不同运行状态的特征向量
利用小波包分解提取的能量在不同频带内数值相差也很大,必须对原始数据进行无量纲化处理,使每一指标值统一于某种共同的数据特性范围。本案采用极值归一化公式把数据压缩到[0,1]之间。极值归一化公式为

式中:X为原始数据;Xmax为原始数据最大值;Xmin为原始数据最小值。
归一化后轴承正常和故障时特征向量对比如图4所示。从图4可以看出,轴承正常和故障运行状态的特征向量有很大的差别。正常工况时,振动加速度信号的能量主要分布在低频段,如频带2和频带4中,这是由周期性振源引起的响应。当轴承的内、外圈出现故障时,振动信号中包含了相应的冲击成分,产生脉冲冲击响应,由于脉冲冲击是一种瞬态激振,将引起轴承系统固有频率的共振[8]。轴承故障产生的冲击响应特征在高频段表现十分明显,这时能量主要分布在频段5、频段6和频段8。故障运行时,轴承内圈故障和外圈故障能量分布也有所区别:轴承外圈出现故障时频段8的高频能量激增值大;而当轴承内圈出现故障时频段8的高频能量激增值相对较小。这是由于当滚动体与内圈损伤点接触时产生的脉冲力要通过滚动体与外圈的界面传播后才作用于外圈,产生了能量损失,所以脉冲力幅度肯定要比前者小得多。轴承不同的故障冲击将会导致不同的振动响应信号,也就是说,不同的故障类型对应有不同的频带能量的分布特征,这表明应用小波包分解提取信号的能量分布信息作为信号的特征向量能很好地表征轴承的运行状态。

图4 轴承正常和故障时特征向量对比图
同理,将待诊断的轴承运行状态信号进行特征量提取,作为待诊断样本,最后将9个标准样本和1个待诊断样本共同组成诊断样本集:
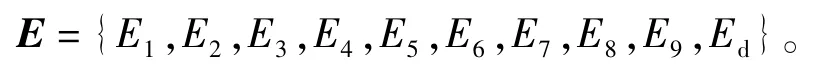
提取的不同运行状态的特征向量矩阵E为:
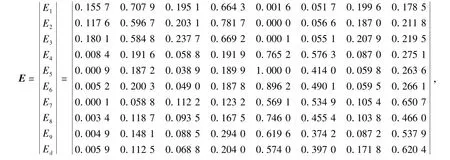
式中:E1,E2,E3为正常运行状态的标准样本;E4,E5,E6为内圈故障运行状态的标准样本;E7,E8,E9为外圈故障运行状态的标准样本;Ed为待诊断样本。
3 故障诊断
采用模糊聚类分析方法[9-10]完成故障诊断。首先采用绝对值减数法对矩阵E进行标定,其定义为:

式中:rst为相似系数,表示样本Es与Et之间的亲疏关系;C为系数,应适当选取,为了使0≤rst≤1,取C=0.308。求出诊断样本集E中任意两个样本之间的相似系数,并组成模糊相似矩阵R,再根据传递闭包法得到诊断样本集的模糊等价矩阵R=R4:

采用λ截矩阵法对模糊等价矩阵R进行聚类分析。对于任一λ∈[0,1],分类时Rλ中各元素改为这样取值:大于或等于λ的元素都改取为1,小于λ的元素都改取为0,根据Rλ中1与0的排列情况进行分类。结果表明:λ∈(0.850 65,0.858 83)时分类和故障诊断的结果最为准确。如λ=0.858 8,得到λ截矩阵R0.8588为:

可见,截矩阵R0.8588将诊断样本集分为3类:{E1,E2,E3},{E4,E5,E6},和{E7,E8,E9,Ed},其中待诊断样本Ed属于轴承外圈故障运行状态。
4 结束语
针对滚动轴承故障诊断的高频带分解至关重要的特点,提出一种把信号无泄漏、不重叠地分解到相邻的独立频段上的小波包能量谱技术,以提取轴承运行状态特征。同时针对轴承运行状态所表现出来的征兆具有模糊性的特点,提出一种基于模糊聚类的故障诊断方法。试验表明,该方法获得的结果与轴承运行状态有很好的一致性,利用此方法能有效地监测轴承运行状态,对故障类型做出准确判断,效果理想。
