基于有限元的连杆衬套过盈分析求解
2010-07-25范校尉樊文欣冯垣洁
范校尉,樊文欣,冯垣洁
(中北大学 机械工程与自动化学院,太原 030051)
1 连杆衬套配合结构分析
高速柴油机中连杆和活塞销都是钢件,在活塞销与连杆小头之间采用全浮式连接时,通常在连杆小头孔内以一定的过盈量压入减磨青铜衬套或铁基粉末冶金衬套,用以减小磨损和提高使用寿命。连杆衬套与活塞销及连杆配合如图1所示。由于装有连杆衬套,在维修时,只需更换磨损的衬套即可,既经济又简便。连杆衬套与连杆小头孔为过盈配合,与活塞销为间隙配合(适当的间隙,用以形成油膜,起到润滑作用)。当衬套压入座孔后,其外圆柱面和连杆小头孔之间存在着很大的径向压力,衬套由于受压,内孔将产生收缩变形,造成衬套内孔与活塞销的配合间隙发生变化,改变了原来间隙的配合性质,甚至造成装配困难[1-3]。因此,只能重新铰孔或镗孔以达到孔公差的要求和解决不便装配的问题。为了保证连杆衬套内孔和活塞销的配合间隙,衬套的变形及其内孔公差的确定至关重要。在产品设计时,也考虑到衬套压装时变形造成的影响,一般都凭经验适当放大衬套内孔的公差,没有一定的理论作为依据。因此,通过合理的理论推导,找出一种计算孔径收缩量ε的正确计算方法,对于修正孔径加工尺寸公差,免去修刮程序,提高工作效率有很大意义。
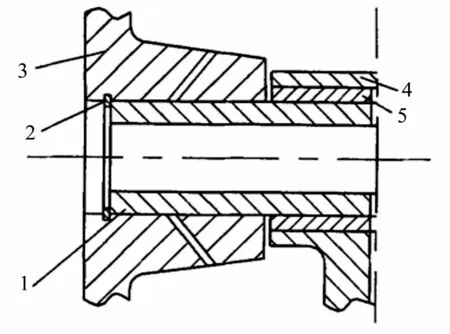
图1 连杆衬套与活塞销、连杆的装配图
柴油机工作时,衬套与连杆小端在较高压力作用下不停运转。在高压工作条件下,随着使用期限增长,一些衬套与连杆小头间会出现微动磨损,即衬套与连杆小头发生了周期地相对运动,并且受到温升和衬套塑性变形的影响,两者间的过盈量会出现蜕减[4-5]。严重时,连杆与衬套出现大的相对滑动,对发动机的性能产生很大影响。因此设计合理的过盈量,才能使衬套与连杆小头在周期性工作中不发生相对运动。而且过盈量对衬套的孔径收缩有很大影响,合理地选取过盈量能得到较佳的孔径收缩量,对满足衬套与活塞销间隙配合所需的间隙值,形成油膜,润滑轴承具有很好的作用[5]。
2 过盈配合计算
2.1 衬套几何尺寸及材料
根据结构设计,确定连杆衬套结构尺寸为:连杆衬套内径d=40 mm;外径D=44 mm,材料为QSn7-0.2,连杆小头外径d2=90 mm。
2.2 连杆衬套受力分析
2.2.1 过盈配合压力
衬套与连杆小头孔过盈配合如图2所示。可以看出,由于圆筒的几何形状及载荷均对称于筒的轴线,变形与应力亦为轴对称,故轴向应力、应变均为零[6]。由弹性力学理论计算可知,配合后产生的径向均布应力为:

图2 连杆衬套过盈配合尺寸及产生的应力分布
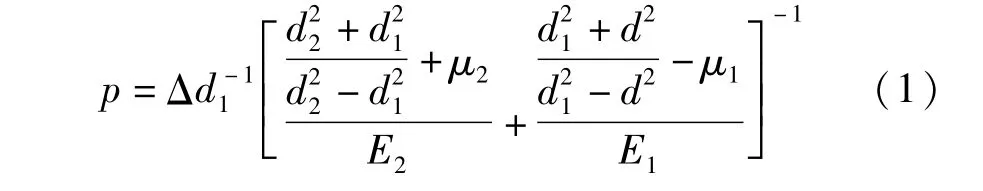
式中:p为配合后径向均布应力,MPa;Δ为衬套压配过盈量;μ1为衬套材料的泊松比,μ1=0.33;μ2为连杆材料的泊松比,μ2=0.24;E2为连杆材料的弹性模量,E2=2.1×105MPa;E1为衬套材料的弹性模量,对于锡青铜E1=1.1×105MPa;d为衬套内径;d1为连杆小头内径;d2为连杆小头外径。
2.2.2 应力求解
对于轴对称问题,一般在极坐标下建立平衡微分方程组。沿半径方向的正应力为径向应力;圆周方向的应力,即衬套受压而产生的拉应力或压应力,称为环向正应力或周向应力。
由拉梅公式可得连杆衬套的应力为:
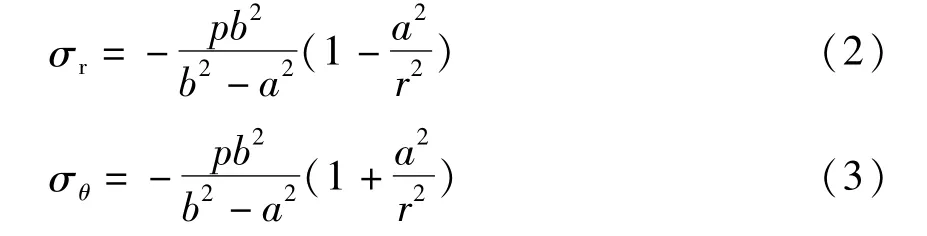
式中:σr为径向应力;σθ为周向应力;a为衬套内半径;b为连杆小头内半径;r为径向变量。
则,当r=a及r=b时,由(2)式和(3)式分别得连杆衬套的内、外壁应力为:

式中:σr1,σr2分别为衬套内、外壁径向应力;σθ1,σθ2分别为衬套内、外壁周向应力。
2.3 压配过盈量计算
压配过盈量不同于工作过盈量。工作过盈量即由于工作温度与装配温度的不同所引起的过盈量的变化。本案未根据工作过盈量计算分析,只分析压配过盈量。
由于衬套厚度T=2<D/20=2.2 mm,因此,过盈量按薄壁圆筒与厚壁圆筒弹性过盈配合计算。对于过盈量的计算,应严格地计算变形量,衬套以平面应力求解,连杆小头以平面应变求解。
对于连杆衬套,装配压力是外压力,则它的外径收缩量为:

连杆衬套是以过盈配合紧固在连杆小头的轴承座孔中,以防止在工作过程中出现松动现象。为此,根据连杆衬套装配所需的最小和最大许用应力值的要求,确定其装配过盈量和外径的公差。
如上所述,连杆衬套的设计要求应满足:

式中:σθ2为衬套外壁压配周向应力值;[σtmin]为装配最小许用应力,通常可取[σtmin]=70~190 MPa;[σtmax]为装配最大许用应力,通常可取[σtmax]=σ0.2,其中σ0.2为衬套材料0.2%的屈服极限。
若取压配过盈量Δ=0.05 mm,由上述式子可得:p=21.929 3 MPa,σθ1=-258.319 2 MPa,σθ2=-236.390 0 MPa,ud1=0.045 7 mm,ε=0.047 0 mm。
由上述计算结果得知,|σθ2|=236.390 0 MPa,满足衬套设计的要求。
3 衬套装配有限元分析
3.1 ANSYS接触问题
利用ANSYS有限元法软件强大的后处理能力,可以对连接后应力的分布、形变的范围、装配时材料的应力变化进行非常直观地分析。适当的过盈不但可以增强连接效果,而且可以提高材料的强度。对于目前成熟的有限元软件来说,连杆衬套和连杆小头孔的过盈连接的设计相当容易实现。因此基于ANSYS软件对发动机连杆衬套的过盈配合(0.05 mm)进行了有限元分析,分析配合中产品是否产生了变形,确定所选配合是否合适。
ANSYS中对接触问题推荐了3种单元类型,分 别 是SOLIDl85(3D 28Node),TARGE170(32DTarget Segment)和CONTA174(32D 82Node Surface 2t02Surface Contact)。其中,TARGE170与CONTA174适用于接触面较为复杂的可变形曲面或柔体。本例中最合适采用SOLID 185三维8节点单元类型。其优点在于8个节点的分布能真实有效拟合弹塑性材料的变形,可通过网格划分的疏密来重点控制应力集中区域,在过盈配合区域网格划分较密集,以满足计算精度;在远离应力集中区域网格较为稀疏,提高计算效率。
本接触问题属于面面接触[4],在涉及到两个面的接触问题时,很自然地把一个面作为目标面,一个面作为接触面,对刚体-柔体的接触,目标面总是刚性的,接触面都是柔性的,这两个面合起来叫做接触对。在分析中,将使用接触单元TARGE170和CONTA174来模拟接触对[7]。如图3所示,为连杆衬套与连杆小头端接触形成的接触对。接触单元的单元类型在分析过程中使用接触向导时可以自动添加。

图3 有限元分析形成的接触对
3.2 仿真分析
由于连杆衬套的对称关系,分析采取1/4模型,并在衬套和简化的连杆小头的4个径向截面上施加轴对称边界约束条件,在连杆小头的外径表面施加位移约束[7]。在创建接触对的过程中,选取摩擦系数,摩擦系数的存在对配合面间的接触应力影响很小,本分析中指定摩擦系数为0.2。接触刚度选择非对称矩阵,接触刚度对过盈配合的影响较大,接触刚度越大,接触压力越大,因此基于理论值的计算分析,接触刚度的处罚系数应合理选取;在分析选取中,穿透容差对过盈配合的影响也很大,穿透容差的变化只是在计算精度上有一个很小的增加,而使计算时间成倍增加是不经济的,故穿透容差选取0.1已能给出足够的精度。增大接触刚度处罚系数通常会相应地减小穿透,而使接触应力有很大变化。综合考虑,本分析指定接触刚度的处罚系数为0.1。
运用ANSYS进行建模,对过盈量为0.05 mm情况下的接触问题进行分析计算,对衬套装配仿真的流程图如图4所示。
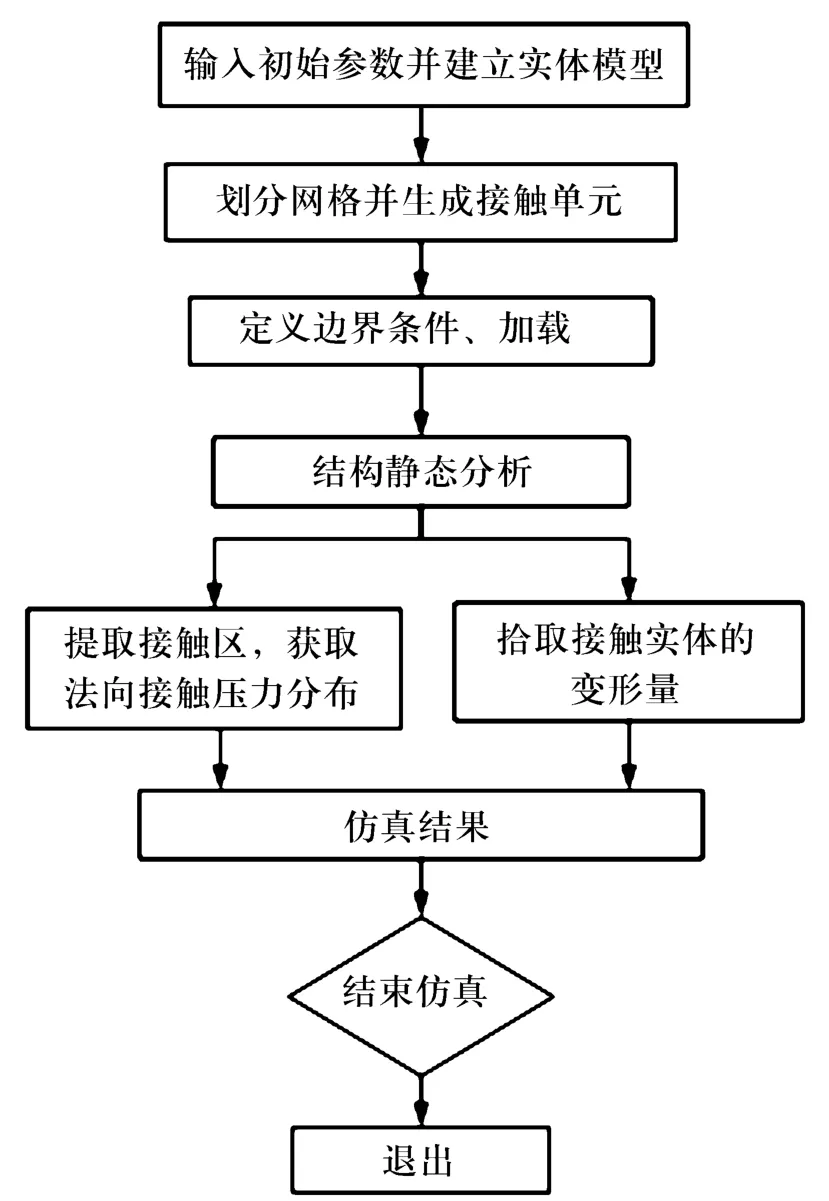
图4 ANSYS仿真流程图
结果分析得出的应力图及衬套的变形图如图5~图10所示。由图可知,衬套与连杆小头过盈配合的接触压应力在整个接触面处并非相等,而是在边缘处获得最大接触压应力;在衬套与连杆小头孔配合处,小头端应力分布不均,径向应力和周向应力均呈现环形分布。

图5 接触压应力分布图
应力集中现象是过盈配合中常见的问题[8],从有限元分析结果可以看出,衬套的径向应力和周向应力在边缘处分布不均,出现应力集中现象。由图10可知,在边缘应力的影响下,衬套在边缘处的收缩变形量与径向方向上相比较小。

图6 径向应力分布图(柱坐标x方向)

图7 周向应力分布图(柱坐标y方向)

图10 衬套径向收缩变形
过盈配合的边缘应力集中程度与连杆小头端的外径有关,在过盈量、连杆衬套的长度、衬套外径以及连杆小头宽度一定的情况下,连杆小头端外径越大,应力集中越严重[8]。
表1给出了仿真数值与理论值的比较。
图8 衬套径向应力分布图(柱坐标x方向)

图9 衬套周向应力分布图(柱坐标y方向)
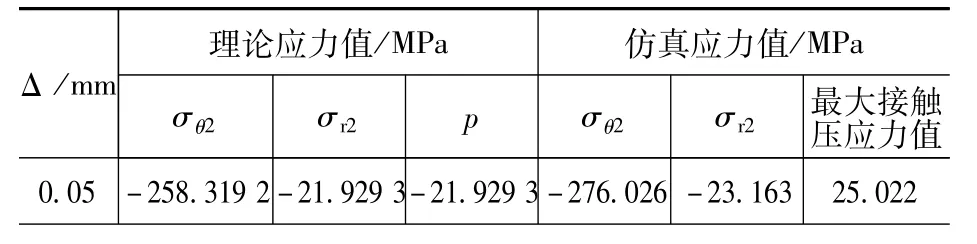
表1 Δ=0.05 mm时的衬套应力值比较
而当理论过盈量Δ=0.05 mm时,内、外半径收缩量理论值与仿真值比较如表2所示。

表2 衬套内、外径收缩量比较
通过表1、表2可知,当过盈量为0.05 mm时,仿真应力值与理论应力值相差很少。衬套内、外半径收缩量的仿真值与理论值有一定的误差,但都保证在6%以内,这些误差主要是单元本身、网格划分、单元离散、几何、边界范围和计算模型处理方法等的误差,都较小。
4 结束语
有限元方法可以充分考虑边缘应力集中的影响,因而,比弹性力学的理论计算方法更真实可靠。有限元合理的仿真分析计算值可以很好地与弹性理论计算值相吻合,不仅验证了该连杆衬套与连杆小头端压配过盈量选取0.05 mm是合理的,而且为进一步求解该型号连杆衬套压配过盈量的合理取值范围提供了方法。
由分析计算出的衬套内径收缩量,对确定衬套内径公差具有指导性作用,为以后衬套与活塞销配合的间隙取值分析提供参考依据。
