线接触弹流脂润滑的数值分析及其应用
2010-07-25于玫,黄平
于 玫,黄 平
(华南理工大学 机械与汽车工程学院,广州 510640)
弹性流体动力润滑(elasto-hydrodynamic lubrication,EHL)(以下简称弹流润滑)问题,从数学本质上讲,需联立求解流体润滑方程(Reynolds方程)、固体表面弹性变形方程、润滑膜几何方程、润滑剂黏度方程和密度方程[1],由于弹流系统的复杂性和强烈的非线性,其几乎不可能求得解析解。弹流润滑的完全数值解就成为全面了解弹流润滑机理和特性的有效途径[2]。
在弹流润滑研究中,所讨论的流体大多是Newton流体,即流体的运动规律符合Newton的推断:黏性剪切应力与剪切应变率成正比[3]。润滑脂具有较强的非Newton流体特性,因此其弹流问题的理论研究更加复杂。随着弹流理论研究的不断深入和弹流应用的推广,基于非Newton流体的弹流润滑研究日益受到关注。文献[4]对脂润滑弹流问题进行了全面的理论分析和试验研究,推导出了适用于Herschel-Bulkley流变模型的一维润滑方程,用分区解法求得线性弹流润滑完全数值解。特殊工况下使用的滚动轴承的接触润滑分析技术在近年来取得显著进展[5]。然而由于脂润滑弹流问题的复杂性,目前能见到的对脂润滑数值分析的研究还不多[6]。这里以Ostwald模型为基础建立脂润滑控制方程,运用多重网格法对等温线接触脂润滑弹流润滑方程进行求解,并以轿车轮毂轴承为例,分析了主要工况参数对润滑膜压力分布和润滑膜形状的影响。
1 轮毂轴承润滑脂流变特性本构方程
这里研究的轮毂轴承为圆锥滚子轴承,其常采用润滑脂实现终身润滑。在弹流脂润滑中,脂润滑膜的重要特征是分层流动,即内层无剪切流动,外层为剪切流动[3]。描述润滑脂流变特性的本构方程目前主要采用Ostwald,Bingham及Herschel-Bulkley 3种模型[7]。文献[8]通过大量试验认为国产润滑脂的特性符合Herschel-Bulkley模型,它含有3个参数。而这里认为该模型的特例就是Ostwald模型,两者的特性有较大的共性。文献[9]认为,工业上80%的广义Newton体均可用Ostwald模型,它仅需确定2个参数,使用简单,因此被广泛采用。所以,这里以Ostwald模型为基础建立脂润滑的控制方程。Ostwald模型的本构方程为:

式中:τ为剪切应力;ϕ为塑性黏度;u为润滑膜流动速度;z为润滑膜厚度方向;n为流变指数;γ·为剪应变率。
严格说来,流变参数ϕ和n都应是温度和压力的函数,对于等温润滑问题不考虑温度的影响,而流变参数与压力的关系通常按简化处理,即认为n与压力p无关[10]。
另外,密度的变化对脂润滑弹流计算的影响较小,通常在弹流脂润滑研究中,假设润滑膜为不可压缩介质[3]。
2 数值分析与求解
2.1 经典脂润滑Reynolds方程的修正
根据(1)式,由文献[4]得等效Reynolds方程为:


2.2 脂弹流润滑其他方程
线接触接触体的长度和曲率远大于接触宽度,可认为属于平面应变状态,相当于平直的弹性半无限体受分布载荷作用[11],如图1所示。表面上各点沿垂直方向的弹性位移为:
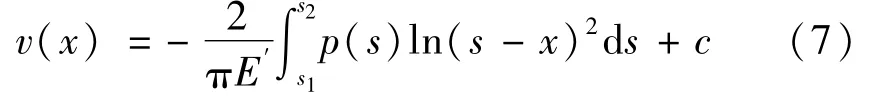
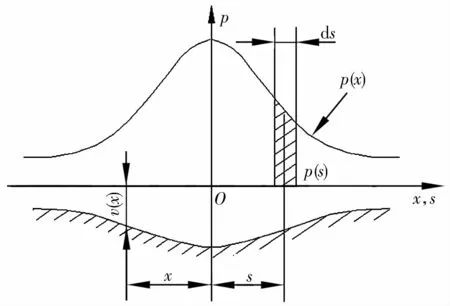
图1 线接触弹性变形
式中:s是x轴上的附加坐标,表示任意线载荷p(s)ds与坐标原点的距离;p(s)为载荷分布函数;s1和s2为载荷p(x)的起点和终点坐标;c为待定常数。
如图2所示,将(7)式与润滑膜压力作用下的弹性变形叠加,可以求得膜厚方程为:

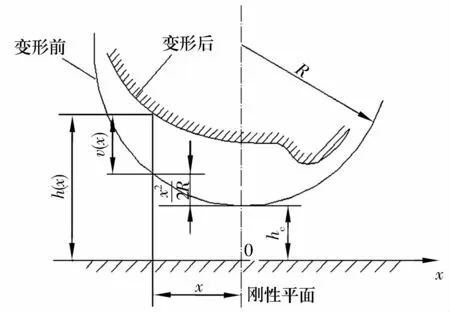
图2 润滑膜的间隙
Roelands提出了较符合实际的等温条件下的黏压关系式:
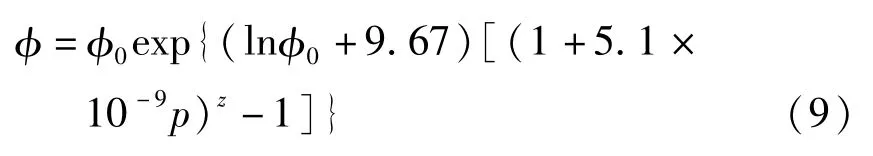
式中:z为试验常数,近似为0.1~1.5。
2.3 基本方程的无量纲化
在数值分析前,需要将线接触润滑基本方程无量纲化[12]。无量纲膜厚方程为:

脂润滑状态是处于动态的变化过程,分析脂润滑弹流一般针对润滑脂在经过剪切稳定后的流变参数相对稳定的状态[13]。用多重网格法计算(6)和(10)~(12)式组成的方程组[7]。迭代过程包括压力修正和载荷平衡所需的刚体位移的修正,这些都是在某一特定网格下进行的[14]。此处对较轻的压力进行修正时采用Gauss-Seidel迭代法;当压力较大时,由于采用这种方法容易发散,因此采用Jacobi双极子迭代法。两种方法同时使用,从而解决了脂弹流润滑的入口区压力变化剧烈和接触区载荷难以平衡的问题,较好地得到问题的收敛数值解。
3 计算结果与分析
根据运算结果可以对圆锥滚子轴承的弹流润滑进行分析。图3是基于表1的工况参数下,载荷、速度、流变指数n分别对润滑膜形状和润滑膜压力分布的影响示意图。图4反映了工况参数对润滑膜最小厚度和最大压力的影响。
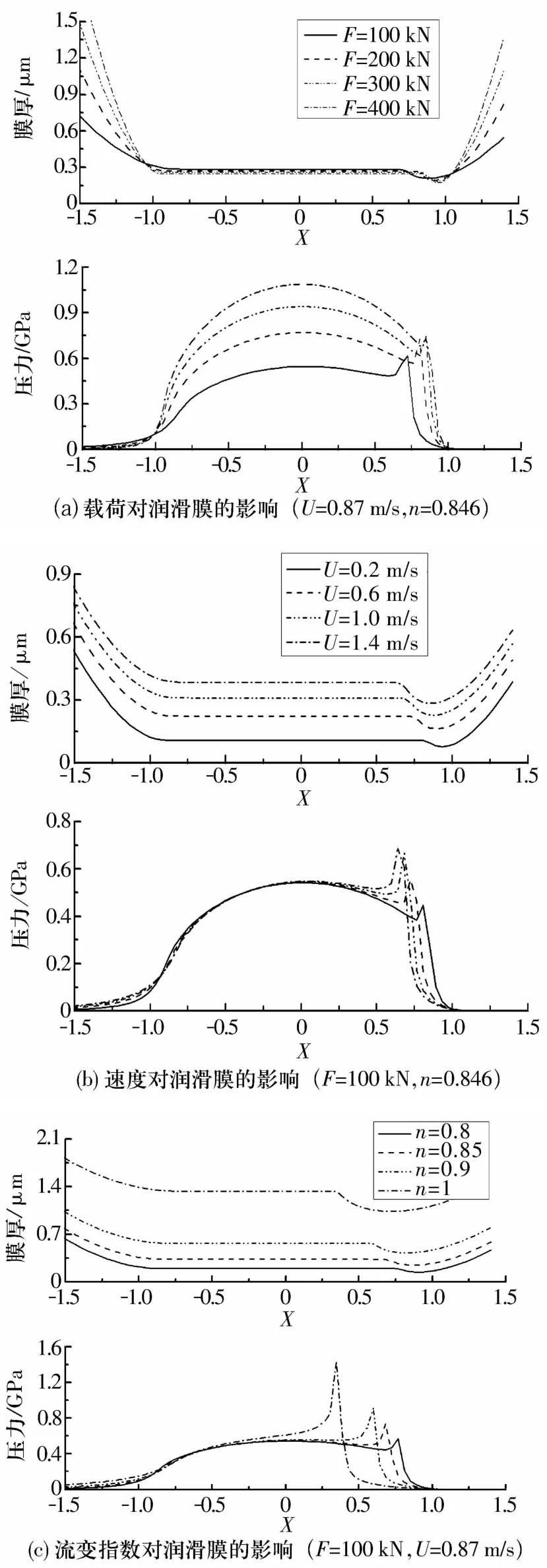
图3 工况参数对润滑膜的影响
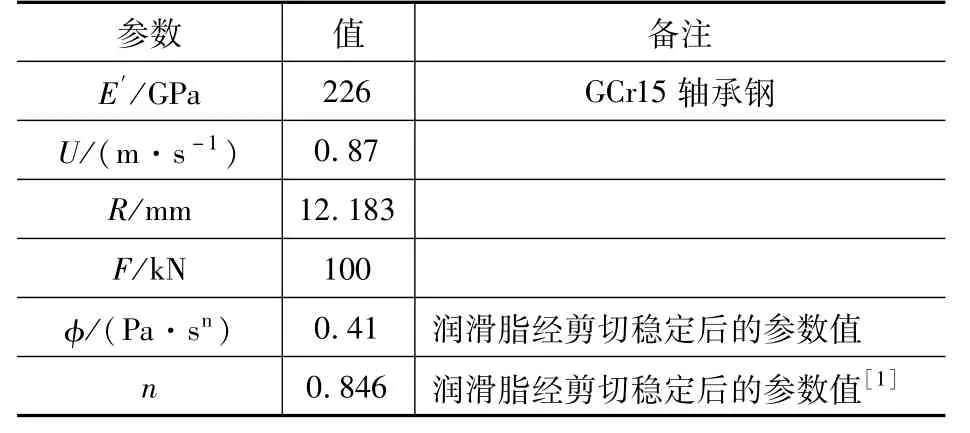
表1 工况参数
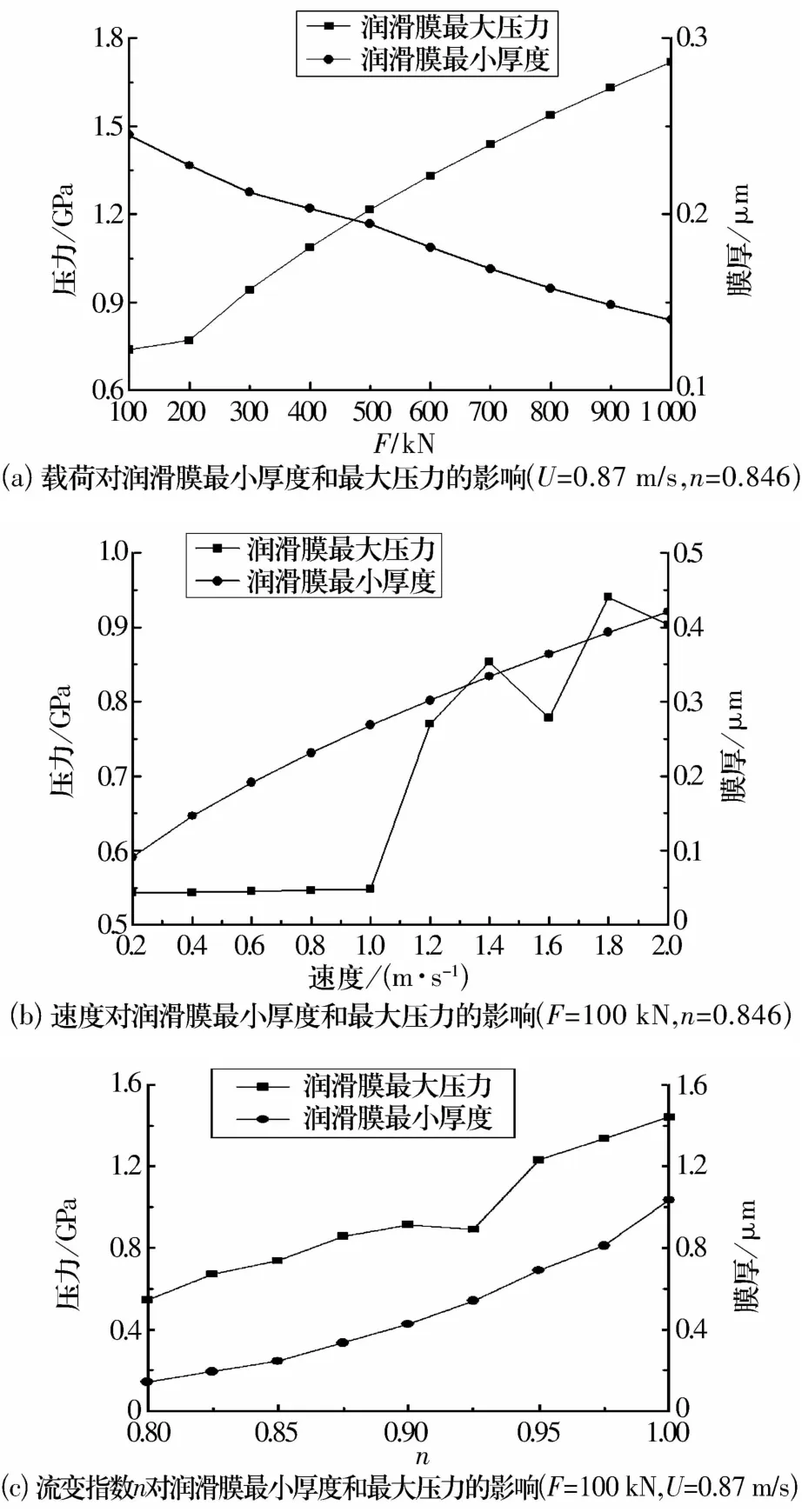
图4 工况参数对润滑膜最大压力和最小厚度的影响
从图3中可看到:(1)脂润滑弹流膜厚形状和压力分布与油润滑情况相似。脂润滑弹流膜具有与油润滑膜相同的二次压力峰和出口区的颈缩现象;(2)载荷的变化对润滑膜压力分布有显著影响,但对润滑膜厚度的影响比较小。在轿车轮毂轴承可能的承载条件下,随着载荷的减小,二次压力峰的高度降低,其位置向入口区移动。在接触区中部,润滑膜压力接近于Hertz应力分布,润滑膜呈近似平行状。在二次压力峰对应处,润滑膜开始收缩,形成出口区的颈缩现象;(3)当速度增加时,膜厚相应增加,润滑膜的平行部分缩短,二次压力峰的高度增加,其位置也向入口区移动。很显然,卷吸速度增大(轴承转速提高)有利于形成良好的弹流润滑膜,从而让轴承处于良好的润滑状态;(4)轴承在一定的承载和卷吸速度条件下,随着流变指数n的增大,二次压力峰的高度升高,其位置向入口区移动,膜厚相应增加。
从图4中可看到:(1)润滑膜的最大接触压力随着载荷的增大而增大,最小膜厚随着载荷的增大而减小,并且都呈近似线性关系;(2)当卷吸速度增大时,润滑膜的最小厚度和最大压力都随之增大,并且也都呈近似的线性关系;(3)润滑膜最大接触压力和最小厚度都随着n的增大而增大,所以n越大越有利于形成良好的弹流润滑膜。
4 结束语
对经典等效脂润滑Reynolds方程存在的问题进行了修正,解决了计算不确定问题。利用轮毂轴承参数,编制程序对不同流变参数条件下的弹流脂润滑进行了计算,结果合理。在一般的工况条件下,计算得到的膜厚在弹流润滑解的范围之内,并且润滑膜压力分布与形状均存在二次压力峰和颈缩现象。最大压力和最小膜厚随工况参数的变化趋势符合实际。这表明文中给出的求解滚子轴承的脂润滑线性弹流问题的方法是可行的,能够较好模拟滚子轴承脂润滑情况,可为开发轮毂轴承提供数值分析手段。
