Weibull定时截尾情形下的矩估计性能

2010-07-25冯自立陈晓阳顾家铭

轴承 2010年9期

冯自立，陈晓阳，顾家铭

（1.上海大学轴承研究室，上海 200072；2.上海天安轴承有限公司，上海 200233）

试验是掌握产品性能最具说服力的手段，其关键在于建立和确认产品性能的概率分布。普遍认为投入试验的试件越多，估计结果越精确，但由于受时间和资金的限制，产品的可靠性试验不仅不能保证大的样本量，还必须采取截尾试验方案。在实践中定时截尾试验多于定数截尾试验。Weibull分布常被用于描述滚动轴承的疲劳寿命，然而对Weibull分布参数估计的研究，大多集中于完全样本试验［1-2］和定数截尾试验。文中通过MonteCarlo法研究矩估计量在小样本量（样本量不超过10）定时截尾情形下，对Weibull分布参数的估计性能。

1 小样本量Weibull定时截尾数据的特性

通过MonteCarlo方法［3］研究Weibull分布下的小样本量定时截尾数据，发现有以下规律［4］：（1）在一定的样本容量和形状参数β下，使得某一失效数出现概率最大的截尾时间，可以是某一区间上的任意取值；（2）对于同一样本结构（n，r）（n为样本容量，r为失效数），不同Weibull分布（形状参数β相同，尺度参数η不同）下的截尾时间区间端点与尺度参数的比值相同。将形状参数等于1时，使得n＝10的各样本结构出现概率最大的截尾时间范围列于表1。

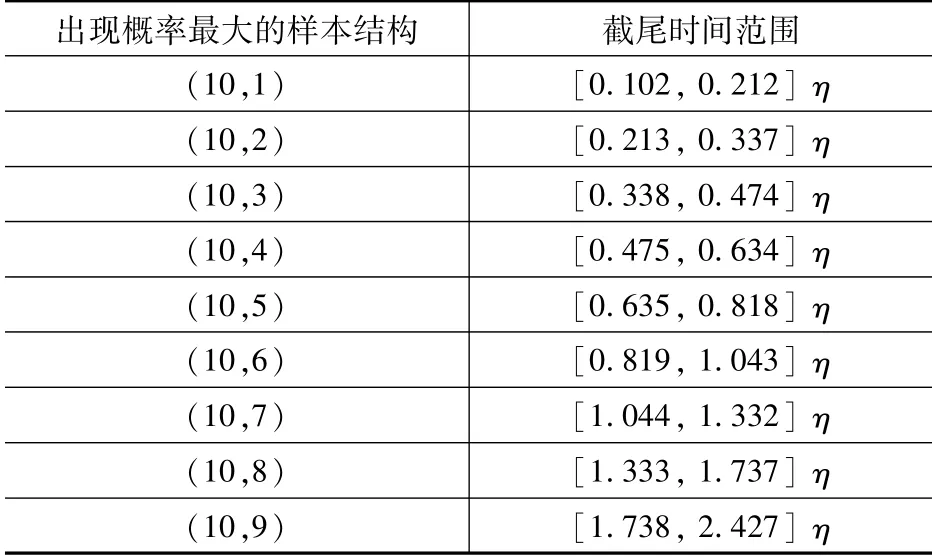
表1 样本结构与对应的截尾时间范围

2 常用估计方法

通常可采用Weibull概率纸图估计法、最小二乘法和极大似然法对Weibull分布下的定时截尾数据进行估计。最小二乘法改善了图估计法易受人为主观因素影响，精度不高的缺点，在实践中应用广泛。但是最小二乘法有一个基本假设［5］，即每个样本点都包含了关于未知母体的相同信息量。然而从Weibull分布母体得到的顺序统计量中，前几个随机变量的离散程度大于后续的随机变量。通过对样本点合理加权可以改善对所有试验数据“一视同仁”的不足。文献［5］通过引入一个中间随机变量，成功解决了计算样本点加权系数的问题。

对于截尾情形下寿命服从Weibull分布的试件，可在各个截尾样本上用1-F（t）＝exp［-（t／η）β］代替概率密度函数与失效样本所对应的概率密度函数值相乘，求出似然函数。

根据极大似然原理可以得到关于βMLE（形状参数β的极大似然估计）的超越方程：

式中：ti（i＝1，2，…，r）为失效时间。方程的左端是βMLE的严格减连续函数，可采用二分法进行迭代求解。在高截尾的小样本量定时截尾数据情形下，（1）式的计算不易收敛。

以从W（1，1）（β＝1，η＝1的Weibull分布母体）中抽取的容量为10的定时截尾样本为例，形状参数的极大似然估计量在各个样本结构下（均保证10 000次有效模拟计算）的5%，50%和95%分位数与截尾时间（表1）的关系如图1所示。

图1 形状参数极大似然估计量的分位数与截尾时间（均为无量纲）的关系

由图1可知：在高、中截尾场合（r＝2～6），极大似然估计量的分位数基本不随截尾时间的变化而改变；在低截尾场合（r＝7～9），极大似然估计量的50%和95%分位数随着截尾时间的增加明显减小。这一规律同样出现在其他样本容量所对应的低截尾场合。最小二乘估计量和加权最小二乘估计量在截尾时间区间上同样有这一规律。为便于比较估计量的性能，对于同一失效数，均取使其出现概率最大的截尾时间区间的左端点所对应的估计量分布进行分析。

以对来自于W（1，1），容量为10的定时截尾样本估计为例，用箱线图表示形状参数的最小二乘估计量、加权最小二乘估计量以及极大似然估计量在各失效数下的90%分布区间（在各样本结构下对3种估计量均保证10 000次有效模拟计算），见图2。

图2 估计量的90%分布区间箱线图

由图2可知：（1）随着失效数的增加，各估计量的精度均在提高，最小二乘估计量与加权最小二乘估计量逐渐趋于无偏（中位数意义上），而极大似然估计量逐渐变大；（2）极大似然估计法精度最高，加权最小二乘法次之，最小二乘法精度最低。

3 矩估计

3.1 矩估计原理

极值分布属于位置-刻度分布族，其分布函数为：

若A～W（β，η）（随机变量A服从形状参数为β，尺度参数为η的两参数Weibull分布），则ln A服从极值分布，其中参数μ＝lnη，σ＝1／β。

考虑位置-刻度分布族的好处就在于对定时截尾情形下的数据可以采用矩法进行估计［6］。文献［7］利用Weibull分布与极值分布之间的转换关系首先研究了Weibull分布下定时截尾数据的矩估计问题，并证明了其构造的形状参数与尺度参数的矩估计量具有强相合性。

中间变量h（p）为［6-7］：

式中：p＝P（X≤T）（设随机变量X服从Weibull分布）。

文献［7］给出的形状参数与尺度参数的矩估计量为：

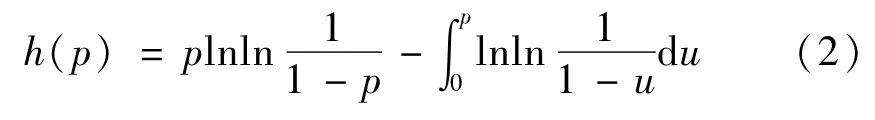
式中：T为截尾时间；采用pE（pE＝r／n）作为p的估计，计算出h（pE）作为h（p）的近似值。

为方便使用，给出样本容量10以内所有样本结构对应的h（pE），见表2。

表2 小样本量下的h（p E）值

3.2 矩估计性能

在低截尾场合下，矩估计量的5%，50%和95%分位数同样随着截尾时间的增加而减小。以对母体为W（2，1）的截尾样本（10，9）估计为例，其矩估计量的分位数随截尾时间变化的曲线如图3所示。

对于不同的失效数，取其对应的截尾时间区间左端点上的极大似然估计量和矩估计量的分布进行比较。

对来自于W（2，1），容量为10的定时截尾样本进行估计（在每个样本结构下均保证10 000次有效模拟计算），形状参数的矩估计量与极大似然估计量的90%分布区间如图4所示。

图3 低截尾场合下形状参数矩估计量的分位数随截尾时间（无量纲）变化的曲线

图4 估计量的90%分布区间箱线图

由图4可知：（1）在小样本量定时截尾情形下，矩估计随着失效数的增加逐渐变大；（2）矩估计与极大似然估计的精度相当。

4 实例计算

以某型陀螺电动机转子轴承小样本精度寿命模拟试验为例说明上述方法的可靠性估计［8］，试验采用定时截尾方案（截尾时间为4 000 h）。共投入8组（每组2套）轴承，其中5组失效，寿命时间依次为：1 313，2 288，2 472，2 506和3 382 h，其余3组截尾。分布拟合优度检验结果表明，可以接受该型轴承精度寿命服从Weibull分布的假设。分别采用极大似然估计法（1）式和矩估计法（3）式对寿命数据进行估计，结果见表3。