区间平滑在船用INS/GPS姿态组合导航系统事后评估中的应用
2010-07-25陈俊杰信冠杰王战军严航
陈俊杰 信冠杰 王战军 严航
(1.海军92323部队, 青岛 266000; 2.海军工程大学导航工程系, 武汉430033;3.华中科技大学电子信息工程系, 武汉 430074)
1 引言
惯性导航系统定位误差随时间积累的特性导致定位精度的降低,利用高精度的舰船运动参数对其进行状态估计和标校显得尤为必要,评估结果可对整个导航设备的工作状况做出评价,为改进导航系统性能提供方向。
动态情况下,组合导航系统实时卡尔曼滤波只利用了时刻K和K以前的观测信息[1],为获得更高精度的舰船运动参数,更好的评估系统工作状态,采用离线区间平滑处理算法,该算法利用了观测时间间隔内全部观测信息,就滤波精度而言,较卡尔曼滤波为优。
姿态信息的引入,可以提高INS误差状态的可观测性[2]。本文将测姿型GPS和中低精度惯导相结合构成综合导航系统,采用文献[3]的滤波模型,以舰船INS/GPS位置、速度、姿态综合导航系统为例进行仿真分析,并比较了滤波和区间平滑的处理效果,结果表明,增加姿态信息的区间平滑估计精度可以使组合导航系统的姿态测量精度获得大幅度提高,并能克服卡尔曼滤波对平台误差角初期估计精度低的缺点,经该方法处理后的数据可以作为对舰船导航设备工作状态进行事后评估的依据。
2 方案设计
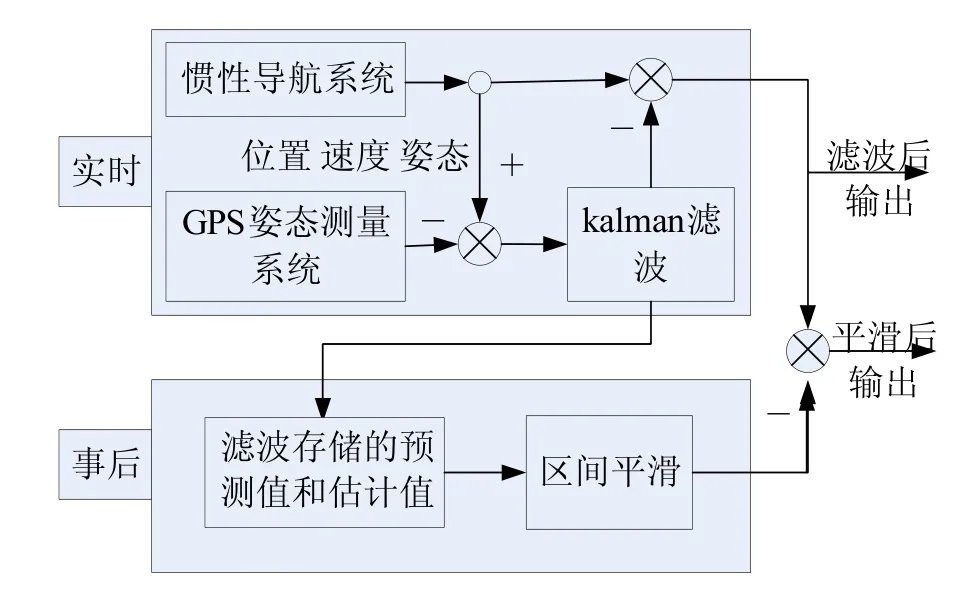
图1 姿态组合导航系统数据流程
对于中低精度的惯导设备来说,将测姿型GPS输出的高精度载体姿态信息作为观测量参与滤波计算,可以提高整个组合系统导航参数估计的精度和速度,滤波过程中储存各时刻状态向量和方差阵的估计值和预测值,之后将数据通过事后平滑模块,获得高精度的舰船航行参数,对惯导系统进行误差校正并将校正后的惯导系统输出作为组合导航系统的输出。组合导航系统数据处理流程如图1所示。
2.1 增加姿态信息后的INS/GPS卡尔曼滤波模型[3]
根据上述思想,为了简化问题,取组合系统状态模型与惯导的误差模型一致[4]。并假定 GPS测量噪声是零均值白噪声,GPS/INS组合导航系统的状态方程为:

惯导误差状态变量取为:纬度误差、经度误差、东向速度误差、北向速度误差、平台的东向失准角、平台的北向失准角、平台的方位失准角,东向和北向加速度计零偏,东向、北向和方位陀螺仪漂移,即:
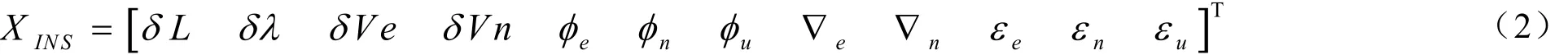
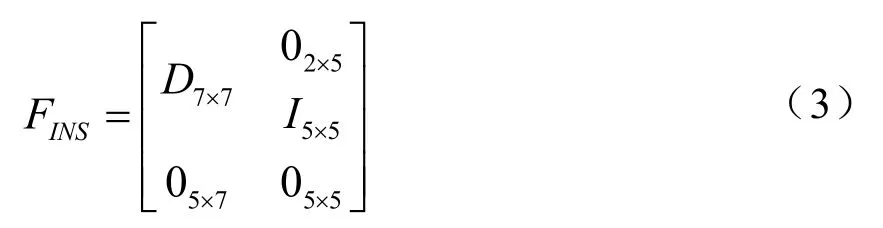
D7×7当中非零项为:
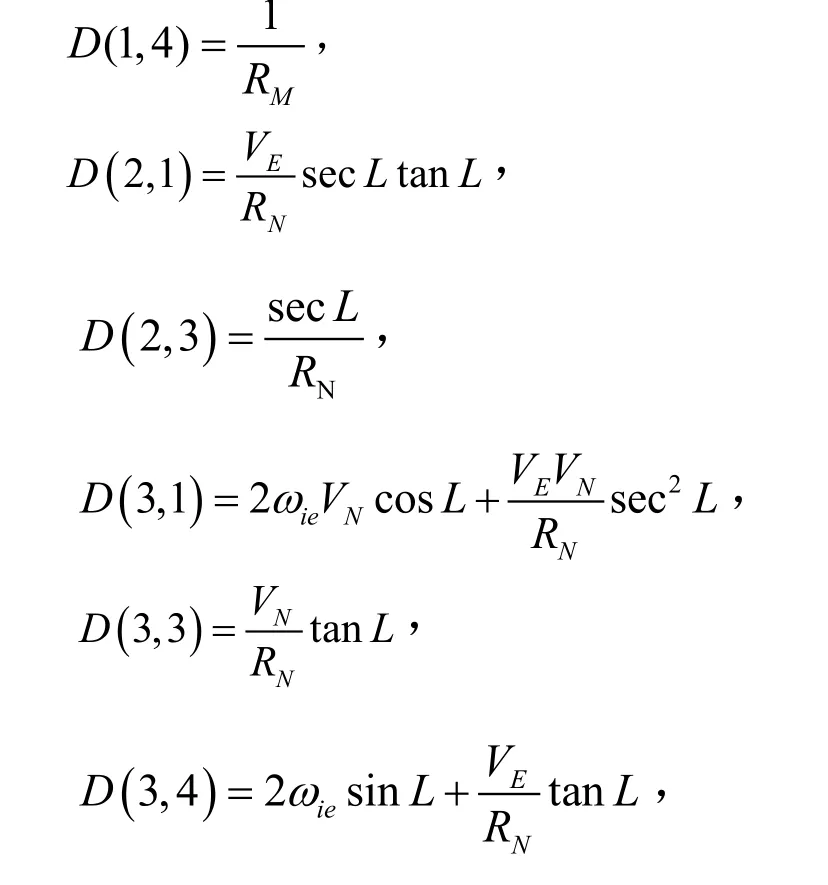
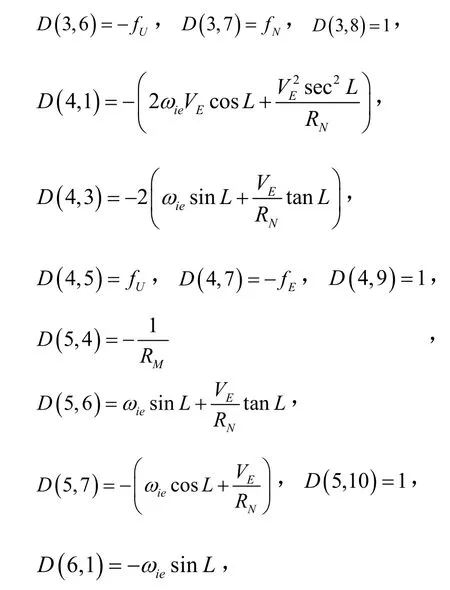

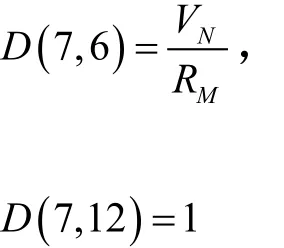
GPS的误差变量取为:GPS导航系统输出的纬度误差、经度误差、东向速度误差、北向速度误差、航向角误差、纵摇角误差、横摇角误差。即:
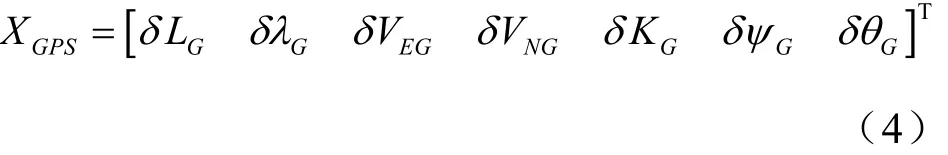
假设GPS的位置误差,速度误差,姿态误差均为一阶马尔可夫过程,则有:
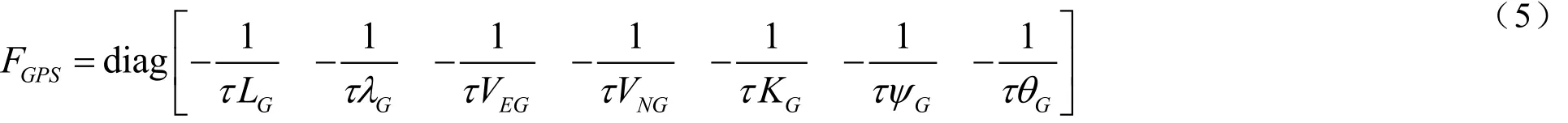
其中相关时间τLG,τλG,τVEG,τVNG,τγG,τψG,τθG分别在100~200 s区间内选取。
系统噪声W选取为均值为0,方差为Q的白噪声:
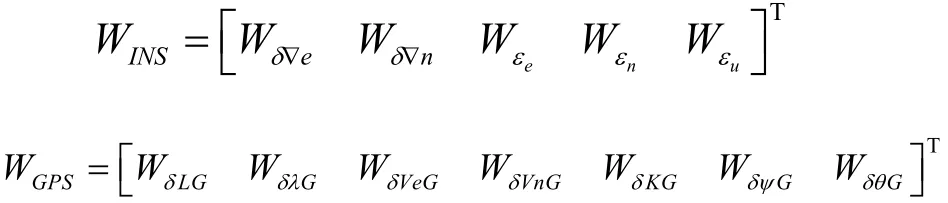
另外,
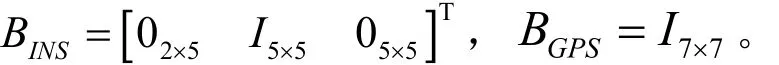
对于GPS/INS组合导航系统的观测方程,考虑数据融合的实际需要,选取位置、速度、姿态组成7维的状态量:

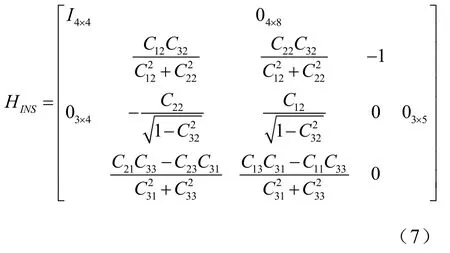
观测噪声VGPS取为均值为0,方差为R的白噪声,并且VGPS和W互不相关。
2.2 最优固定区间平滑滤波器
为了阐明区间平滑估计的原理,给出其计算顺序图,详见图2。
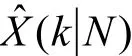
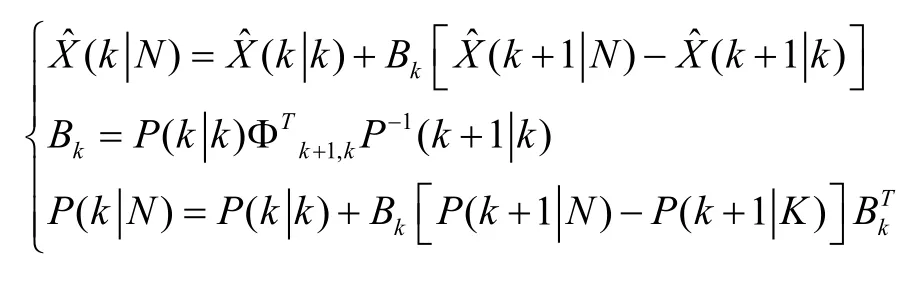
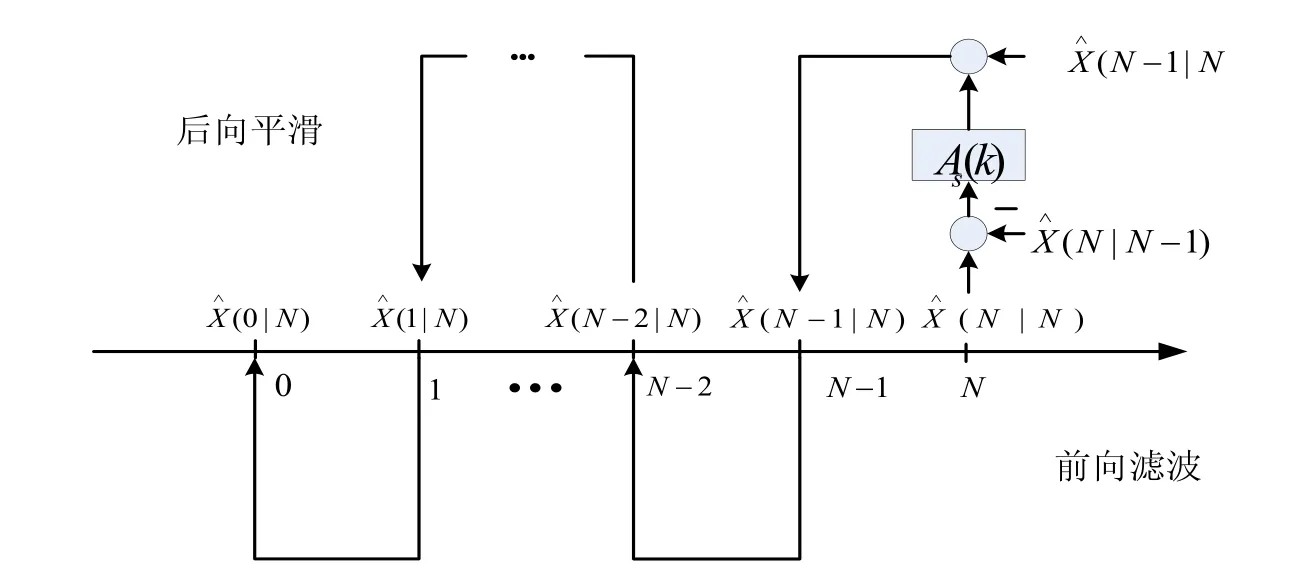
图2 固定区间最优平滑的计算框图
由递推方程和计算流程图可以看出,前向滤波与后向平滑分开进行,先进行N点的前向滤波,再逐点进行后向平滑,由于前向滤波数据处理过程已经消除了大部分的误差,再将滤波结果作为后向平滑的初始值,在利用了包括K时刻以后的全部观测新息的基础上,固定区间平滑算法定位精度要优于前向滤波结果。
3 仿真结果与分析
结合上述模型,本文采用比较最优滤波和区间平滑处理数据之后协方差的方法来评价滤波器的精度,即协方差值越小精度越高[4]。设舰船做匀速直航,航向,横摇角,纵摇角分别为ψ=30°,θ=1°,γ=1°,航速为 10 kn,惯导系统陀螺常值漂移为 0.01 °/h,随机漂移 0.005 °/h,加速度计初始零偏为10-4g,随机零偏5×10-5g,东向、北向、方位失准角取为2', 2',3'滤波周期为1 s。GPS位置误差1 m,东向、北向速度误差0.1 m/s,航向角误差取 2',纵摇角误差取为 40″,在此仿真条件下,滤波估计误差的标准差变化曲线如图3~图11。
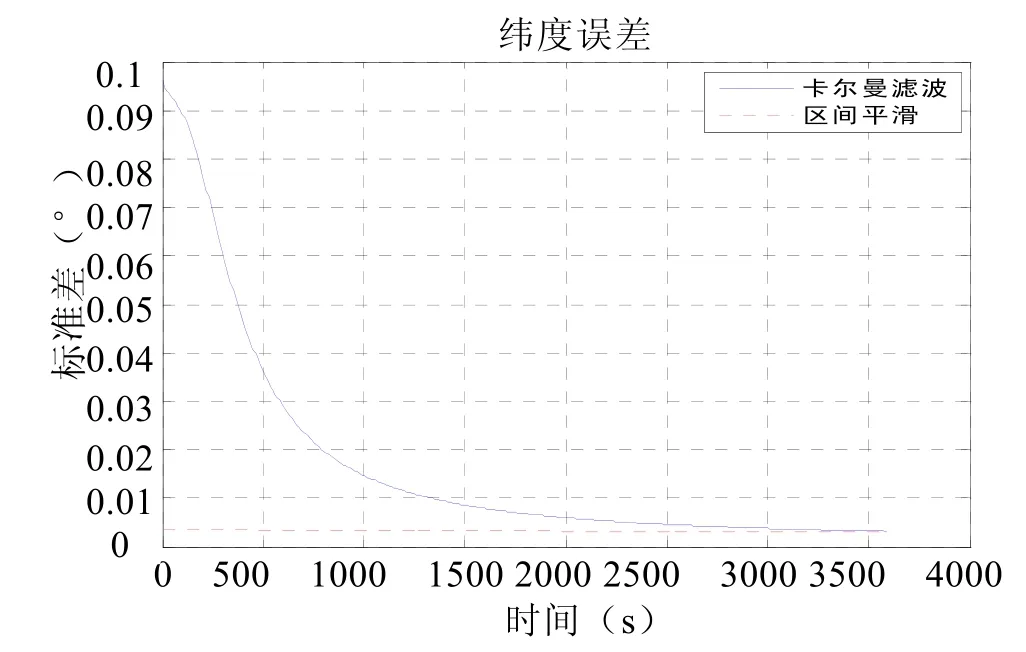
图3 纬度误差曲线
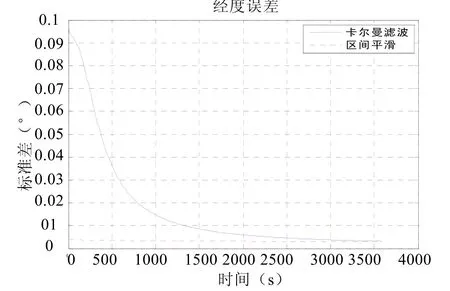
图4 经度误差曲线
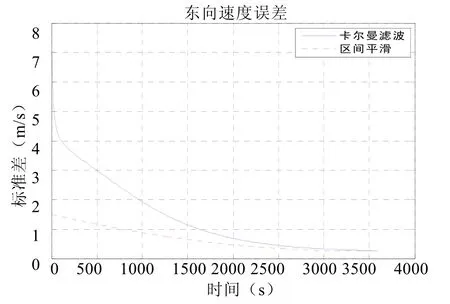
图5 东向速度误差曲线
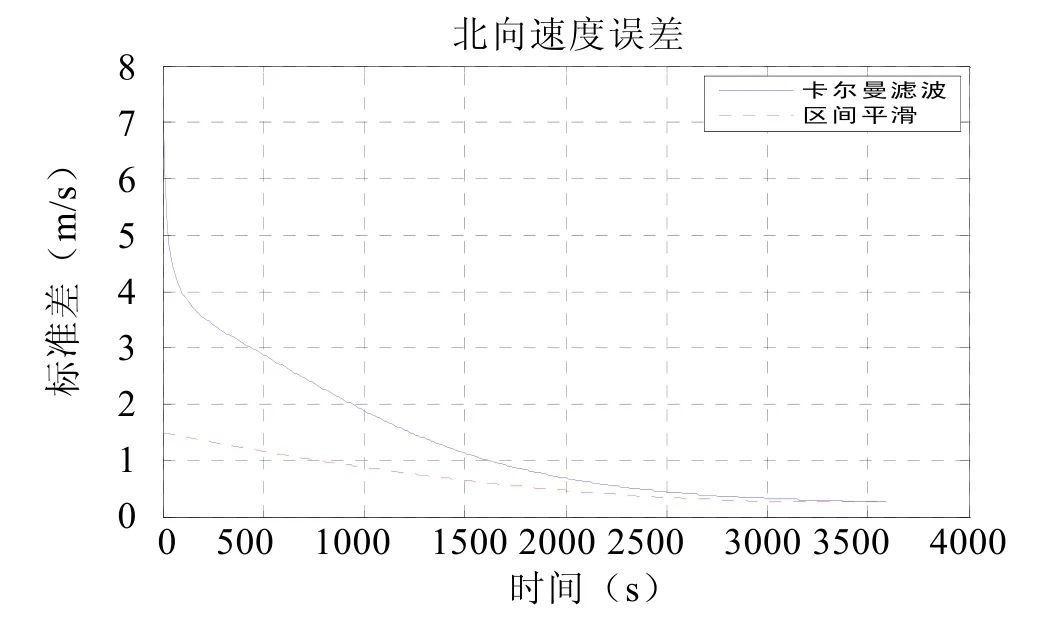
图6 北向速度误差曲线
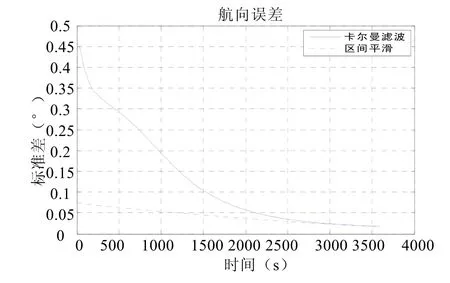
图7 航向误差曲线
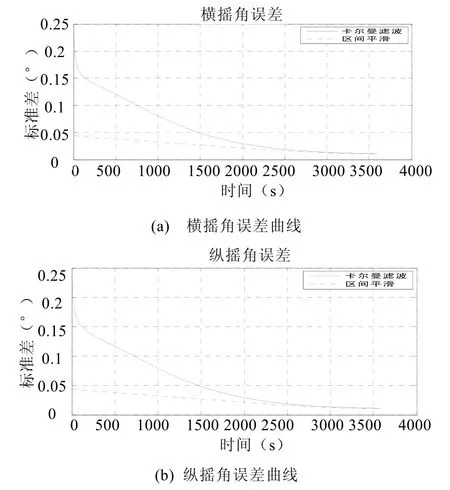
图8
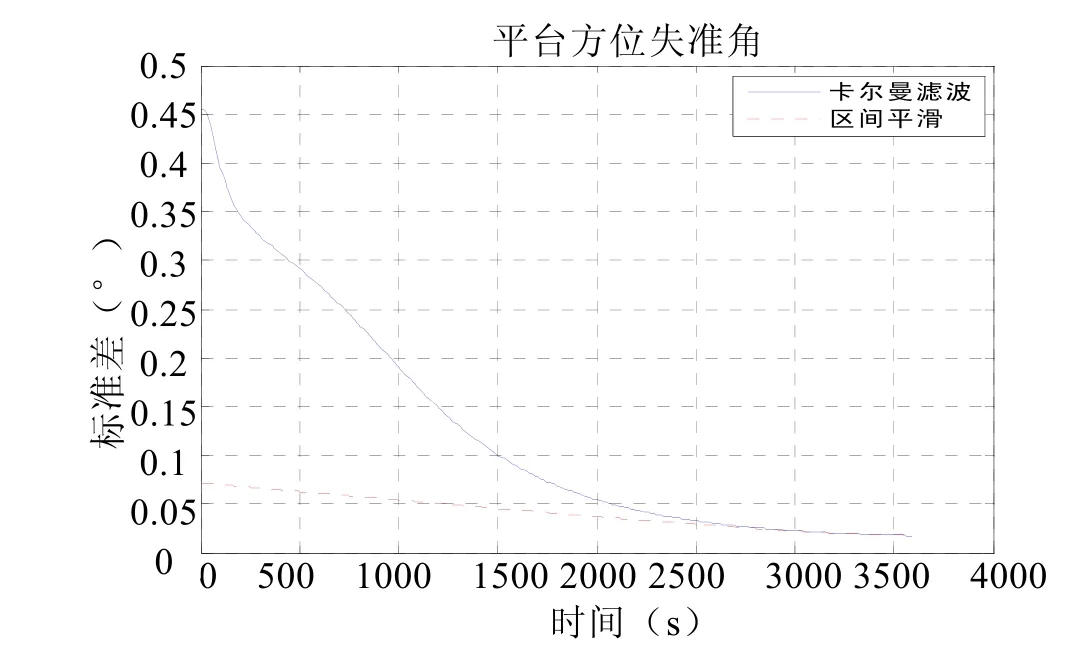
图9 方位平台失准角估计曲线

图10 东向平台失准角估计曲线
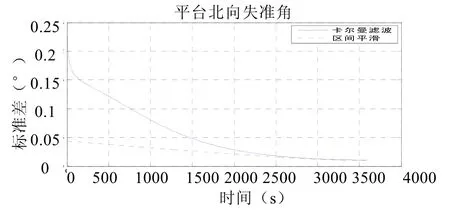
图11 北向平台失准角估计曲线
4 结束语
本文通过对基于惯导/测姿型 GPS组合导航系统模型的具体仿真实现,充分利用观测时间间隔内全部观测信息的区间平滑算法,分析比较了区间平滑和卡尔曼滤波的数据处理精度,获得了更高精度的舰船航行状态参数和航行轨迹,组合效果明显,克服了最优滤波对平台误差角初期估计精度低的缺点,可以作为一种评估舰船导航设备工作性能的事后分析方法。
[1] 王志贤. 最优状态估计与系统辨识[M]. 西安:西北工业大学出版社,2004.62-73.
[2] 张源, 许江宁, 卞鸿巍. GPS姿态测量系统对惯性导航系统误差修正能力分析[J]. 情报指挥控制系统与仿真技术.2005.27(5):96-100.
[3] 杨艳娟, 卞鸿巍, 田蔚风, 金志华. 一种新的INS/GPS组合导航技术[J]. 中国惯性技术学报,2004,(4):23-26.
[4] 邱吉冰, 蒋志翔. 组合导航系统离线信息融合算法[J]. 计算机工程与设计, 2008,29(9):2346-2349.
[5] 曹梦龙, 崔平远. 多模型高精度组合导航算法研究[J]. 系统工程与电子技术,2008,30(7):1304-1307.
