基于因子分析和SE-DEA的港口上市公司经营效率评价

孙柯洋，赵一飞

(上海交通大学船舶海洋与建筑工程学院，上海 200240)

0 引言

企业经营效率是从企业经济活动角度出发的、有别于生产活动的技术效率.王国顺［1]认为，企业经营效率是从企业经营目标的角度考察企业经济活动的投入与产出的关系，是企业经营活动的产出对投入或收益对成本的比值，一般计算式为

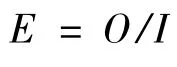
式中:E为企业经营效率;O为产出或收益;I为投入或成本.

通常用财务比率(如投资回报率、资产周转率等)来评价企业经营绩效.但实践证明，各财务比率只能反映1种投入和1种产出的对比关系，而难以全面反映经营管理中的多种投入和产出的综合情况.目前，用数据包络分析(Data Envelopment Analysis，DEA)模型评价公司的经营效率可有效解决该问题:陈军飞等［2]和王春芝等［3]都采用DEA模型对港口上市公司的经营效率进行定量分析.

然而，DEA模型也存在以下不足:(1)投入、产出变量的选择带有主观性，且需满足模型的诸多约束后才能得到有效结果.SMITH［4]认为，减少投入或产出变量能提高DEA效率的区分度，但在小样本情况下，如果重要变量被删除，可能会使样本无法完全反映系统的原有信息，也不能得到准确的效率值.若投入或产出指标间存在相关性，也会对DEA的评价结果产生影响，得到的效率值比真实情况下的DEA效率值小，即会低估效率值.［5](2)在得到多个有效的决策单元(效率值为1)后，无法对其进行充分排序.为改进上述不足，本文尝试提出因子分析(factor analysis)和超效率数据包络分析(Super Efficiency Data Envelopment Analysis，SE-DEA)模型相结合的两步法分析模式，并对我国13家港口上市公司2008年的经营效率进行评价.

1 因子分析与SE-DEA模型相结合的两步法

第1步:采用因子分析提取投入、产出变量，克服一般DEA模型变量选择上的主观性，实现用更少的独立变量反映更多信息的目的，较好地满足DEA模型的诸多约束条件，使得到的效率值能更真实地反映实际情况;第2步:采用SE-DEA模型计算效率值，并对所有决策单元进行充分排序.

1.1 用因子分析提取投入、产出变量

因子分析，又称因素分析，是通过寻找众多原始变量的公共因素，从而简化变量中存在的复杂关系的1种统计方法.它将每个原始变量分解成2部分:一部分为所有变量共同具有的少数几个因子，即公因子;另一部分为每个变量独自具有的因子，即独特因子.因子分析的数学模型［6]如下

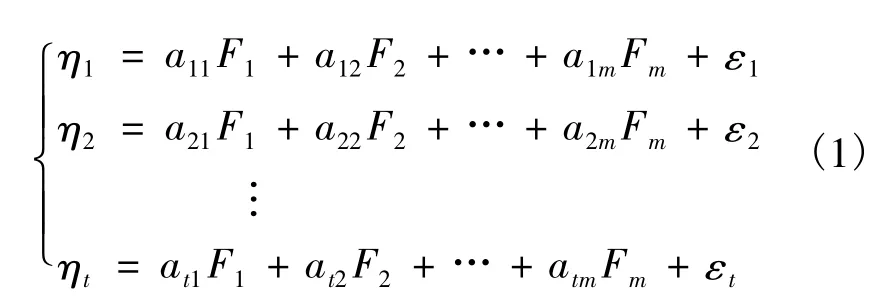
式中:η1，η2，…，ηt为 n 维变量;F1，F2，…，Fm为 n维变量，表示公因子;ε1，ε2，…，εt为 n 维变量，表示独特因子;aij为因数.由于公因子的累计方差贡献率越高，能越多地反映原备选变量中所含的信息，一般认为公因子的累计方差贡献率超过80%，就能反映原备选变量中所含的绝大多数信息，可在后续分析中忽略独特因子.

与主成分分析法相比，因子分析法有2大优点［7]:(1)不是对原有变量的取舍，而是根据原始变量的信息重新组合，找出影响变量的共同因子并化简数据;(2)通过旋转使因子变量更具有可解释性，命名清晰性高.

1.2 用SE-DEA模型计算效率值并充分排序

一般的DEA模型以相对效率为基础，运用线性规划模型研究具有多项投入和多项产出的若干决策单元(Decision Making Units，DMU)的相对有效性.在保持DMU的投入或产出不变的情况下，借助数学规划，将DMU投影到DEA前沿面，通过比较各DMU偏离DEA前沿面的程度评价其相对有效性.DEA模型的数学模型［8]如下

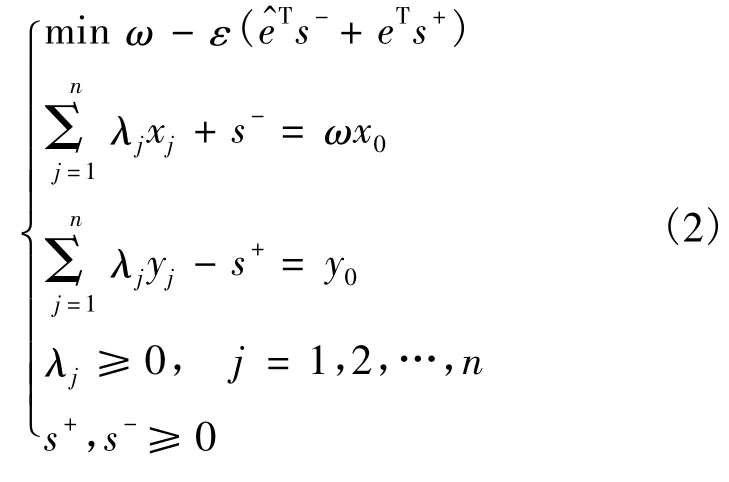
针对一般DEA模型无法比较多个有效DMU之间效率高低的问题，有专家提出SE-DEA模型在评价某个DMU时，通过使该DMU的投入和产出由其他所有DMU的投入和产出的线性组合进行代替的方法，将其排除在外，从而使有效DMU之间也能比较效率的高低.SE-DEA模型的数学模型如下

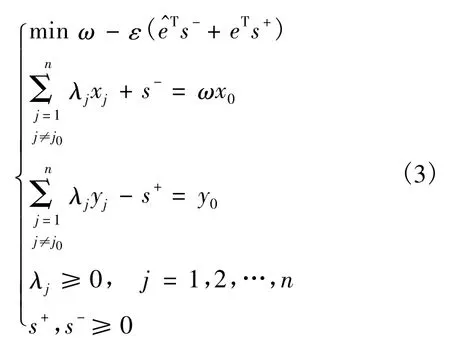
2 港口上市公司经营效率的实证研究

2.1 采用因子分析提取投入变量和产出变量

COOPER等［9]给出投入和产出变量选择的一般要求:(1)对所有的决策单元，投入和产出值可以得到且为正数;(2)投入和产出变量必须反映分析者和管理者的兴趣;(3)不同投入和产出变量的单位可以不一致.根据上述3点原则，在综合国内外研究成果的基础上，本文选择6个备选投入变量(固定资产净额I1，流动资产I2，实收资本I3，营业成本I4，管理费用I5和员工人数I6)以及4个备选产出变量(营业收入O1，营业利润O2，税前利润O3和港口吞吐量O4).同时选取我国13家港口上市公司为研究对象，以各家公司2008年年报的数据为备选变量的原始数据，见表1.

表1 备选变量的原始数据

采用SPSS 13.0对备选投入变量作因子分析，I1，I2，I3，I4，I5和 I6分别对应于式(1)中的 η1，η2，η3，η4，η5和 η6;相关因数矩阵中的所有值都远大于0.3，说明各投入变量的相关性很好;KMO值为0.790，巴特莱特球体检验结果表明相关因数矩阵与单位矩阵有显著差异，说明上述6个备选投入变量适合作因子分析.

表2 正交旋转后备选投入变量的公因子载荷

由表 2 可知，x′1对 I1，I2，I3和 I6这 4 个备选投入变量的影响最大，由于这4个变量都与公司的资源规模直接相关，可命名为资源积累;x′2对I4和I5影响最大，而这2个变量都与公司营运直接相关，可命名为运营投入.

采用同样方法对备选产出变量作因子分析，O1，O2，O3和 O4分别对应于式(1)中的 η1，η2，η3和η4;相关因数矩阵中的所有值都远大于0.3，说明各产出变量的相关性很好;另外，KMO值为0.737，巴特莱特球体检验结果表明相关因数矩阵与单位矩阵有显著差异，适合作因子分析.

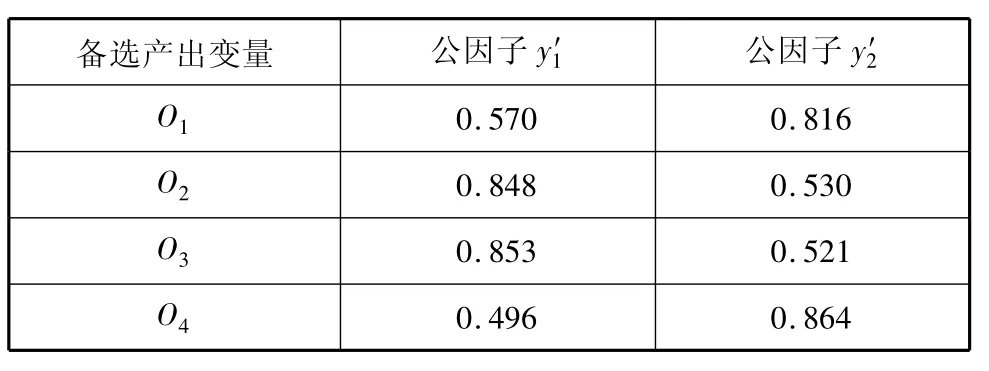
表3 正交旋转后的备选产出变量的公因子载荷

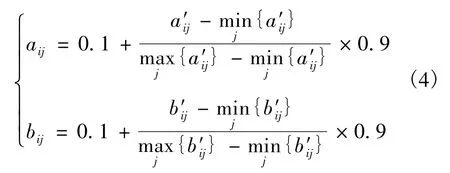
式中:a′ij∈x′i(i=1，2;j=1，2，…，13);b′ij∈y′i(i=1，2;j=1，2，…，13);aij∈xi(i=1，2;j=1，2，…，13);bij∈yi(i=1，2;j=1，2，…，13).

上述变换只对变量的值作数学处理，不影响变量的本质含义，因此处理后的变量仍沿用原变量名称，见表4.

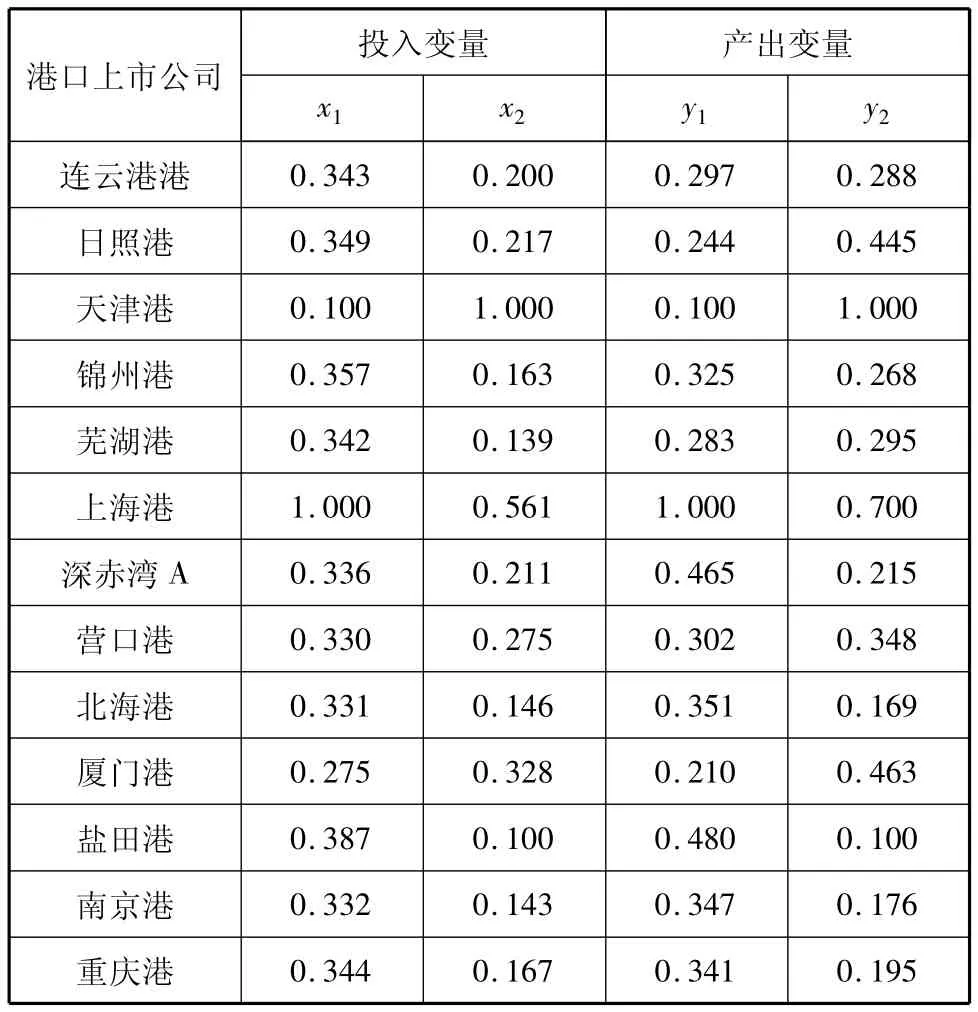
表4 处理后的投入与产出变量

2.2 基于SE-DEA模型的有效性计算

将表4中的投入与产出变量作为SE-DEA模型的投入与产出变量，利用DEA Excel Solver进行计算，结果见表5.

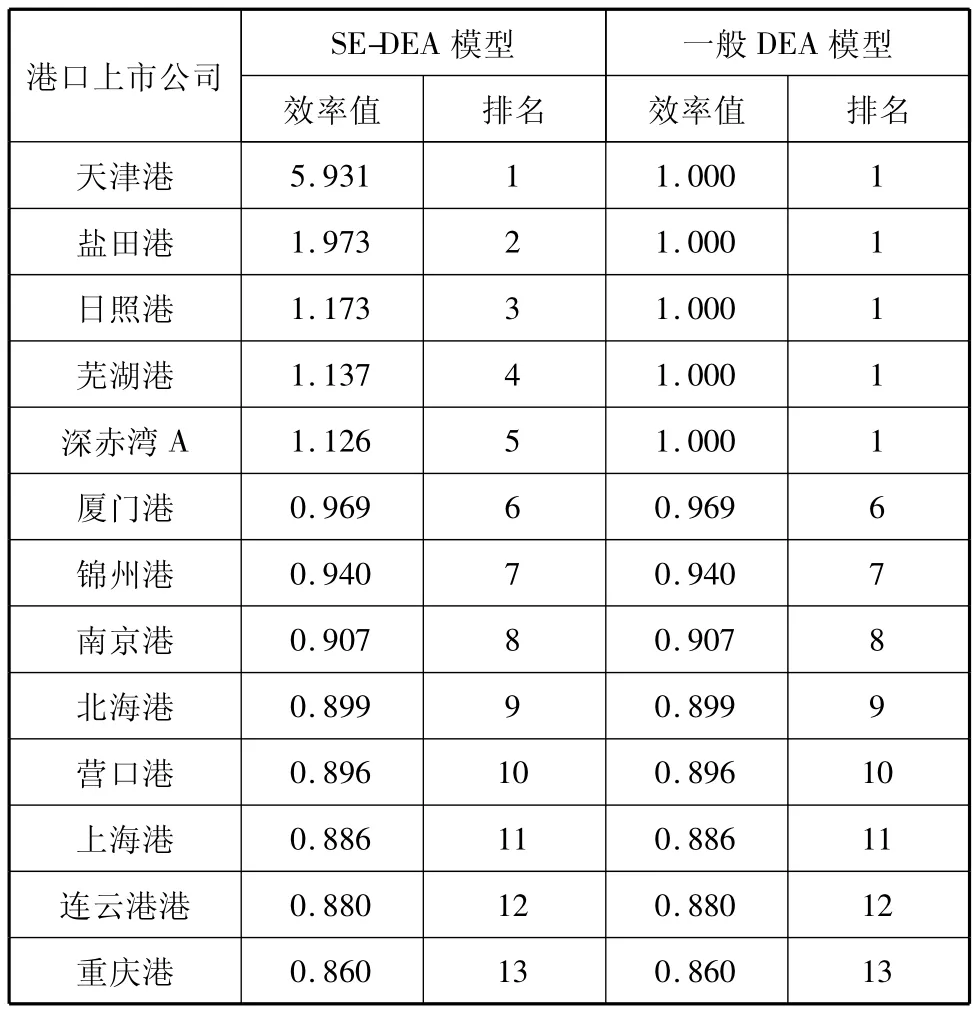
表5 模型计算结果对照

由表5可知，天津港以较明显的优势排在第1位，而重庆港暂居榜尾.一般DEA模型得到5个效率值同为1的港口，而SE-DEA实现对所有港口的充分排序.由于SE-DEA模型仍是1种相对有效的评价模型，得出的结果也是相对效率值而非绝对效率值.

3 结束语

本文为港口上市公司的经营效率评价提供1个新的定量方法，即因子分析与SE-DEA模型相结合的两步法，并综合国内外的研究成果，建立1套备用投入、产出变量体系，在对我国13家港口上市公司2008年的经营效率进行评价时，得到较为理想的结果，具有一定的理论和现实意义.

由于不是任意的备选投入与产出变量都能作因子分析，而且两步法只能得出参评对象的相对效率排序，不能给出造成效率相对优劣的原因，今后还需作进一步的研究.

［1]王国顺.企业经营效率:概念、来源及关系［J].中南工业大学学报:社会科学版，2002，8(3):224-228.

［2]陈军飞，许长新，严以新.用数据包络分析法对港口水运上市公司经营效率的评价［J].上海海运学院学报，2004，25(1):51-55.

［3]王春芝，王凯，马庆国.基于因子分析与DEA的港口行业上市公司经营效率评价［J].西安电子科技大学学报:社会科学版，2008，18(1):110-116.

［4]SMITH P.Model misspecification in data development analysis［J].Ann Operations Res，1997，73(10):233-252.

［5]刘永辉.基于综合变量DEA的商业银行效率评价研究［D].长沙:湖南大学，2007.

［6]李利梅，柳向东.R型因子分析模型描述［J].统计与决策，2003(8):88-89.

［7]李新蕊.主成分分析、因子分析、聚类分析的比较与应用［J].山东教育学院学报，2007(6):23-26.

［8]庄茜，李绍武.改进DEA在港口效率评价中的应用［J].天津城市建设学院学报，2008，14(2):102-105.

［9]COOPER W W，SEIFORD L M，TONE K.Data envelopment analysis:a comprehensive text with models，applications，references＆ DEA-solver software［M].London:Kluwer Academic Publishers，1999:22-23.