基于MRF高斯混合模型的海浪纹理背景目标区域分割

张子丹

(上海海事大学商船学院，上海 200135)

0 引言

海平面背景下的目标区域分割是机器视觉研究中的难点，其主要原因是动态海平面背景和光照使分割出来的前景目标含有大量噪声.另外，海浪剧烈波动引起的相机晃动也会影响目标检测的精度.因此，建立高鲁棒性背景模型是提高动态背景下的目标区域分割的关键.目前较为经典的背景模型有自适应平滑模型［1]、多分辨率多尺度自回归(multiscale autoregressive)模型［2]、高斯模型［3-4]、非参数模型［5]以及卡尔曼预测模型等.上述模型能解决某些特殊场景的目标区域分割，但对于复杂海面背景有一定的局限性，如仅考虑背景的亮度信息，而很少考虑丰富的海浪纹理信息等.本文介绍1种根据海平面背景特点和海浪纹理信息建立的马尔科夫高斯混合模型［6-8]，通过获取图像特征，并假设图像特征遵守正态分布，将分割问题转化为纹理图像的聚类问题，从而分割出海浪纹理背景下的目标区域.

1 海平面特征分析

1.1 海浪纹理分析

由于海浪受环境(风速、光照等)影响而引起的海面变化，反映在二维图像中为亮度和颜色的变化，微视觉模式［9]在海浪纹理中重复出现，因此，海平面波浪纹理区呈现随机排列的多样模式，区别于结构性较强的周期纹理，见图1.

图1 不同特征的海浪纹理图像

海浪纹理分析主要借助纹理基元，图2为不同场景下的海浪纹理基元特点.

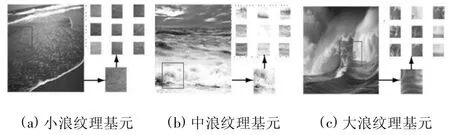
图2 不同场景下海浪纹理基元比较

图2 (a)为微浪纹理，其基元纹理呈现细小纹理特征，但纹理排列未呈现周期性，因此，该场景下的海浪纹理属微纹理［5];图2(b)为中浪纹理，其纹理更不规律，纹理基元较大;图2(c)为大风浪场景下的纹理，其纹理基元更大，基元间的内在运动关系更难以描述.因此，仅依靠基元特性和像素灰度信息分析海浪纹理远远不够，可考虑充分利用纹理的空间布局和统计方法描述海浪纹理.

1.2 海浪纹理背景的高斯模型

可见光下海浪的灰度和颜色内在的相互作用形成海浪纹理图像，图3为可见光下的海浪纹理图像及其直方图.由图3(a)可知，海浪细致纹理图像像素符合多态正态分布;在图3(b)轻浪背景下，海浪开始破碎，呈现较多的反射棱角，因此，直方图分布变得较不规则;在图3(c)中，海浪纹理更不规则，直方图分布更复杂，像素的分布已不符合正态分布.因此，本文根据单模态的思想用多模态思想描述复杂场景中像素点值的变化.［10]

图3 海平面背景的直方图分布

2 MRF高斯混合模型

马尔科夫随机场(Markov Random Field，MRF)模型因其能充分利用空间的信息而广泛应用于纹理分析和模糊聚类，被认为是描述图像像素联合概率分布的有力工具.从随机场的观点看，海面目标的检测问题可看作分类问题，即如何从观测到的灰度图像中获取图像真实类别的标记图像.

2.1 MRF和Gibbs分布

设二维m×n平面图像像素点集合为S={1，2，…，m ×n}，K={1，2，…，Q}为像素的标记集合，Q为类别数.图像分割就是对图像上的每个像素分配1个像素标记集合K中的1个类别v，标记图像为分割后的结果，表示为

可将Y定义为S上的1个MRF.

设图像某像素点r的邻域为ηr(r∉ηr)，S上的邻域系统集合 η ={ηr，r∈S}.如果∀v∈K，r∈S，则像素点r在其邻域ηr中被赋予标记v的概率为P(yr=v|yηr)=P(v)，表示为1个 MRF实现，表示某像素点仅与其邻域系统有关，与邻域系统外的点无关.由于MRF和Gibbs分布的一致性，P(Y)可表示为

像素组 C={(i，q)，i∈S，q∈η}，η 为像素点 q 的邻域系统;β为分割因子，U(y)值越小，实现Y的能量越小，越可能实现.

根据MRF与Gibbs分布的一致性，通过能量函数确定MRF的条件概率，从而使其在全局上具有一致性.通过单个像素及其领域的局部交互，MRF模型可获得复杂的全局行为，即计算局部的Gibbs分布可得到全局的统计结果.

2.2 基于海浪纹理的MRF高斯混合模型

已知所观测的输入灰度纹理图像Y是定义在网格集合S上的，由贝叶斯公式得

式中:P(X|Y)为后验概率;P(Y|X)为Y的条件概率;P(X)为先验Gibbs分布概率.目标的分割就是给定1个特定的y(y是Y的1个实现)，在某种最优准则条件下求得X的1个估计，即求使P(Y|X)最大的分割标记:

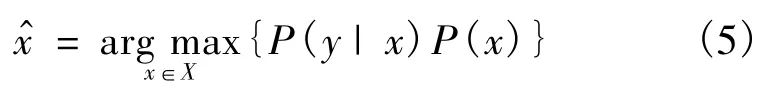
式中:x和y分别为X和Y的样本.假设Y中的每个灰度信息 yr(r∈S)符合高斯分布，参数 θr=(μr，σv)，v=xr(r∈S)，则

由MRF高斯混合模型表达式可得变量X和Y的联合似然概率P(X，Y)=P(Y|X)P(X)，联合概率可进一步表示为

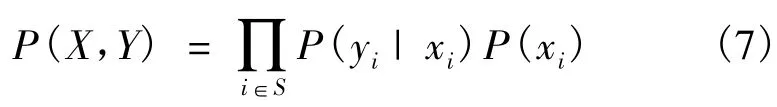
由于y分布独立，变量x和y的联合似然概率为

由文献［9]可知，最优化概率估计问题可转化为能量最小化问题

3 参数估计以及算法步骤

由上述可知，最优化概率估计问题可转化为能量最小化问题，能量最小化问题可转化为求式(8)的最优解问题.由于能量函数U(y|x)为非凸函数，其极小值较多，在类别不定时，不可能通过穷尽的搜索方式得到最优解.图像边界信息的存在以及参数和类标记的相互独立性，使观察数据不完备，因此，选择EM算法［11]从不完备的数据集合里提取参数.设 y～为估计所丢失的数据，则{y～，y}为完备的数据集.通过最大化完全数据对数估计E(log P(x，y|θ))估计新的参数集合θ，再经过E-step和M-step，参数的集合可表示为

式中:t为迭代次数.

EM算法可简单描述如下:

BEGIN

输入图像

步骤0 7×7中值滤波;

步骤1 初始化参数和分割参数以及迭代条件;

步骤2 E-step，用式(5)和(7)，计算 U(x|y)，U(x)，θ，计算后验概率分布Pt(k|yi);

步骤3 M-step，极大化t时刻的期望值，更新t时刻的参数;

步骤4 执行以上步骤，满足迭代条件则停止;

步骤5 中值滤波以及形态学处理.

输出图像

END

4 试验分析

为验证方法的可行性，可对不同纹理下的海浪纹理进行分析.所测试的图片来自网络和课题组，目标是将彩色图像转换为灰度图像.图像的背景为较宽广的水域，因此，设分割类别K=2，分别表示海面背景和船舰目标(以及部分天空背景).由于分割光滑因子β值的选取没有较好的估计模型，试验中的β值均是在反复比较的情况下得到的.为得到较为理想的分割效果，对图像组首先进行中值滤波.由于基于迭代的EM算法对初始值的要求较为敏感，试验中的均值μ0取样本的均值向量.

表1为样本集合的部分训练参数，从中选择较合适的参数作为初始化参数.表1中的object表示图像集合中的船舶集合和落水人员等小目标集合;background表示海浪细致纹理背景模型集合.

表1 样本集合的部分训练参数

由于参数β过大会造成细节的丢失，太小会使邻域信息变弱，难以有效滤除噪声，本文通过多次选择确定β大小.由于微浪纹理较细，为控制分割光滑程度，分割因子β选择0.4.

为表示该算法的可行性，选择几个经典的纹理分割方法与本文方法作比较.图4为经典的图像分割方法和本方法的比较，其中:图4(a)为较细海浪纹理背景下的原始图像，图像场景为对比度较小且受到光照影响的海面背景;图4(b)为GS(Gibbs-Sampler)方法得到结果;图4(c)为基于区域生长和边界信息的分割结果，区域生长方法未能充分利用海浪的空间分布信息而产生过分割问题;图4(d)为改进的OSCU方法［12]，基于直方图的自动阈值选取对于受光照影响较大的海面背景目标区域分割有局限性;图4(e)为本文的试验结果，较前面的几种方法有更好的分割效果，基本能将目标分割出来，并且背景没有过多地被划分到目标区域中.

图4 纹理分割效果对比

为表现本文方法的有效性，用分割正确率(Correct Classification Ratio，CCR)表示分割效果:

式中:C为分割正确率;Nc为分类正确的像素个数，Nt为像素总个数.表2给出各种方法的分割正确率，由表2可知本文方法的分割正确率较其他方法有较大的改进.

表2 不同方法的图像正确分割率

图5给出算法的时间比较，由算法收敛的抽样点得到.文献［12]的OSCU方法因其较为简单，没有大量的迭代运算，快于其他算法;本文算法(改进的MRF方法)虽含有大量迭代运算，但初值取得较为合理，因此算法时间符合要求;基于区域生长和边界分割方法(区域生长方法)由于最初的数据量有限，收敛速度与其他方法相差不多，但随着数据量的增加，收敛性受到较大限制，该算法的时间逐渐增加;GS方法(Gibbs-Sampler方法)虽然有较好的分割效果，但需要进行较多的浮点运算，且要花费较多的时间寻求全局的最优化，算法的实时性较差.

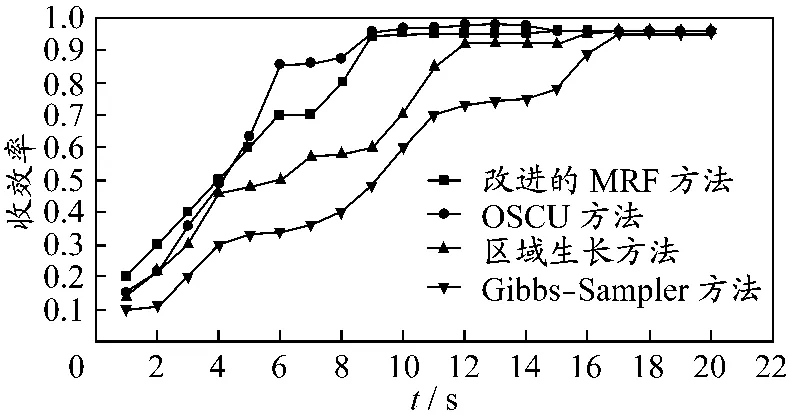
图5 本文算法和传统算法的时间比较

5 结束语

海浪纹理背景下的目标区域分割与传统的场景分割有很大的不同，需要结合海浪的内在纹理形成机制和背景像素的空间分部信息进行分割.本文结合像素空间分布信息以及统计思想提出1种基于MRF高斯混合模型的海浪纹理背景目标区域分割方法.试验结果表明该算法对细海浪纹理分割有可行性，但同时还存在着若干问题，如对于大浪和中浪背景纹理，本方法的分割精确度较低，对于天空背景和地岸等多类别的背景会造成误分割或过分割，需进一步解决和讨论.

［1]LONG W.Stationary background generation:an alternative to the difference of two images［J].Pattern Recognition，1990，23(12):1351-1359.

［2]FRAKC A.Internal multi-scale auto-regression process，stochastic realization ＆ covariance estimation［D].Cambridge，Massachusetts:MIT，1999.

［3]SCAUFFER C，GRIMSON W.Learning patterns of activity using real-time cracking［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，2000，22(8):747-757.

［4]COLLINS R，LIPTON A，KANADE T，et al.A system for video surveillance＆ monitoring［C]//8th Int Topical Meeting Robotic＆ Remote Systems，1999:510-514.

［5]ELGAMMAL A.Non-parametric model for background subtraction［C]//Eur Conf on Comput Vision.London:Springer-Verlag.2000:751-767.

［6]DENG Huawu，CLAUSI D A.Gaussian MRF rotation-invariance features for image［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，2004，26(7):951-955.

［7]KASHYAP R L，KHOTANZAD A.A model-based method of rotation invariance texture classification［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，1986，8(4):472-481.

［8]DENG Huawu，CLAUSI D A.Advanced Gaussian MRF rotation invariance texture features for classification of remote sensing imagery［C]//Proc 2003 IEEE Comput Soc Conf on Comput Vision＆ Pattern Recognition.Madison，Wisconsin，2003:42-48.

［9]ZHANG Yongyue，SMITH S，BRADY M.Segmentation of brain MR images through a hidden Markov random field model and the EM algorithm［J].IEEE Trans on Med Imaging，2001，20(1):46-51.

［10]GEMAN S，GEMAN D.Stochastic relaxation，Gibbs distributions ＆ the Bayesian restoration of images［J].IEEE Trans on Pattern Anal＆Machine Intelligence，1984，6(2):721-741.

［11]HALL N R，HALL D，NASCIMENTO J，et al.Comparison of target detection algorithm using adaptive background models［C]//2005 Int Workshop on Performance Evaluation of Cracking and Surveillance.2005:217-219.

［12]JIN Lisheng，TIAN Lei，WANG Rongben，et al.An improved OSCU method for image segmentation［C]//IEEE ICSP 2006 Proc，2006:159-168.