船底月池流激振荡特性研究

赵尚辉，刘见华

（708研究所，上海 200011）

0 引 言

某型船在船舶运动最小的船中部设置了贯穿船底至主甲板的月池。月池相对于船底而言是一陷落腔，当船航行时，陷落腔附近流场会形成流体剪切层，产生流噪声。同时，月池内流体存在“活塞”和“晃荡”两类振荡现象：“活塞”振荡是流体沿月池深度方向的固有振荡；“晃荡” 振荡是流体液面在月池内的左右振荡现象。当流体剪切层自持振荡频率等于月池内流体振荡固有频率时，就会产生月池内流体耦合共振；船舶航行于波浪上时，当波浪遭遇频率等于月池内流体振荡固有频率时，也会引起月池内流体耦合共振。

月池设置的目的是为了提供一个相对稳定的工作环境，使工程作业不受海上风浪的干扰，但是当有共振现象出现时，月池内流体振荡的幅度将大大增加，当船航行时，共振现象还将产生巨大的阻力，并且在月池内流体大幅晃荡的条件下，船体还将加剧升沉或摇摆运动，从而影响该船的正常航行和工作。

1 船底月池内流体固有振荡特性研究

船底月池内流体存在“活塞”和“晃荡”两类振荡现象。这两类固有振荡的频率仅与月池的开口形式、结构尺寸及吃水有关，与月池口水的流速无关。

1.1 月池内流体活塞振荡频率预报

月池内流体的“活塞”振荡可假设为一直径为R，厚度为H，密度为ρ的圆柱状物体浮在水面沿垂向上下的振动，如图1所示，V为月池外流体的流向。不考虑月池内流体与腔外的质量交换、流体的黏性及其与月池侧壁的摩擦，对月池内流体的固有振荡频率进行计算。

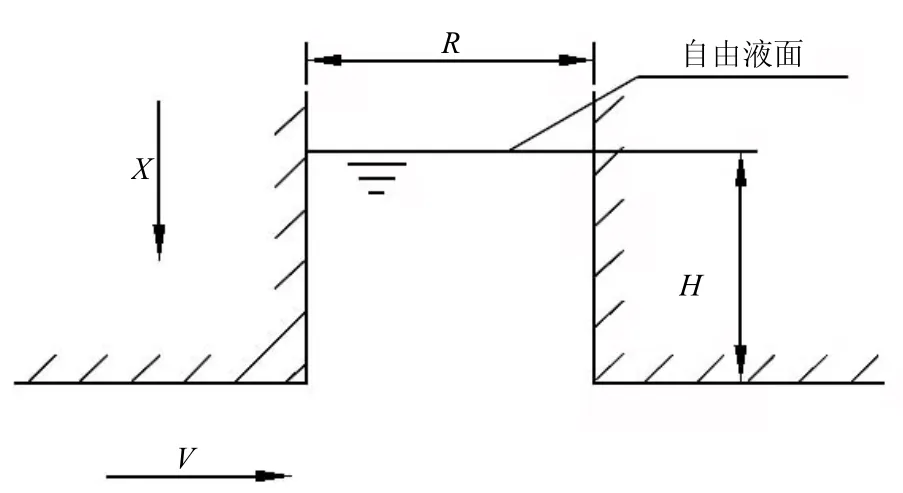
图1 月池内流体振荡频率计算

月池内流体“活塞”振动方程可写为：

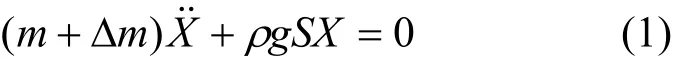
式中：m——月池内流体的质量；

Δm——附加质量；

S——月池横截面面积；

g——重力加速度。

由Morison公式可得浮在水面沿垂向振动的圆柱的附加质量[1]为：

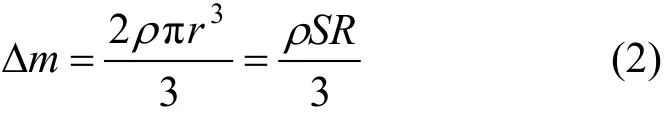
式中：R——直径；

r——半径。

代入式(1)，可得圆形月池内流体“活塞”振动的固有频率公式为：

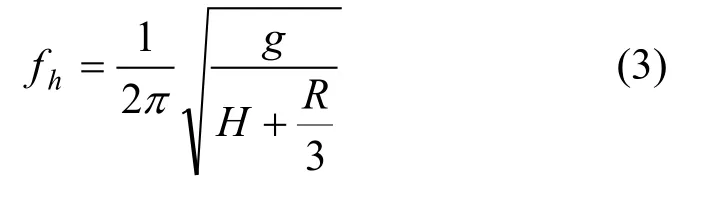
式中：fh——“活塞”振动的固有频率，Hz；

H——月池内吃水深度，m。

应用上式计算了试验研究的月池内流体的“活塞”振荡频率，与试验结果十分接近。因此，利用该式来预报实船月池内流体振荡的频率。实船月池直径R=3.9m，月池内吃水H＝5.3m，则 “活塞”振动的固有频率为fh=0.194Hz。

1.2 月池内流体晃荡固有频率预报

月池内带有自由液面的流体由于外界的激励，在月池内左右“晃荡”，表现为自由液面的正弦运动，图2为月池内流体的首阶晃荡振型图。

不考虑月池内流体与腔外的质量、能量交换，可在月池腔口处设一壁面边界条件，将流体分为月池内、外两部分。月池内流体的晃荡现象与容器内流体的晃荡现象较为类似。月池内自由液面主要考虑二维晃荡，则晃荡频率公式可借鉴容器内液体的二维晃荡频率公式。朱仁庆等[2]给出了在理想流体，不计表面张力，微幅波条件下，长为L，高为H的矩形容器内液体的二维晃荡频率公式为：

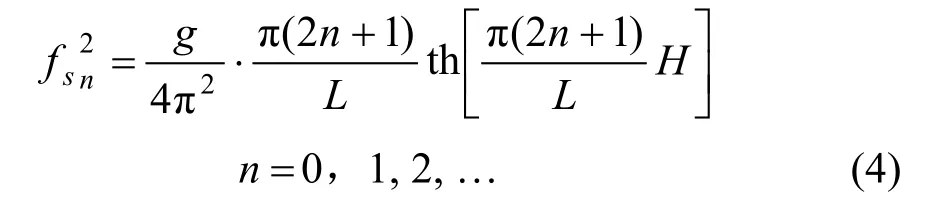
式中：fsn——晃荡固有频率，Hz；

n——晃荡阶数；

L——流向最大跨度，m；

R——月池直径，L=R，m；

H——月池内吃水，m。

则实船月池内流体首阶晃荡频率为0.447Hz。

2 船底月池流激振荡试验研究

为研究流体沿船底流经月池激励的月池振荡现象，开展了船底月池流激振荡试验研究。模型与实船的比例为1∶13，船模中安装圆形月池见图3。

图3 船模中安装圆形月池

月池流激振荡试验时，分为均匀流、波浪和浪流联合作用等三种情况。均匀流和波浪流速从0.4～2m/s，波浪波高从40～80mm，周期从1～3s。

由于月池内有自由液面的存在，月池模型与实船的相似准则采用傅汝得数Fn和 Strouhal数St相似，定义分别如下：

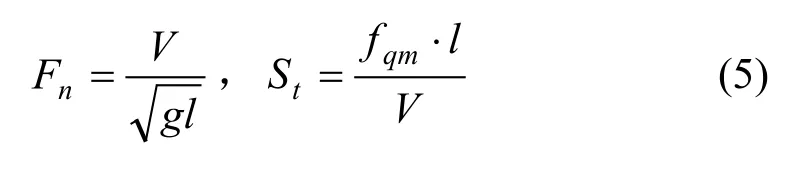
式中：V——航速，m/s；

l——特征长度，对于圆形月池，l=0.8R，R为圆腔直径，m；

fqm——流体剪切层自持振荡的各阶频率，Hz。

通过对普通陷落式腔体的研究可知，在马赫数小于0.2的范围内，当流速超过一临界值时，描述流体剪切层自持振荡频率的Strouhal数St为一定值[3-4]，因此可以利用St的这一特性来推导得出实船月池口流体剪切层自持振荡的频率。

通过对均匀流工况试验结果的分析，可得在均匀流的条件下，月池口剪切层自持振荡的St数为0.55（m=1），0.986（m=2），1.299（m=3），其中m为剪切层自持振荡的阶数。

通过对波浪工况月池流激振荡试验结果的分析，发现月池内的流体在不同波浪周期下表现出不同的运动特性。月池内流体的振荡存在着某临界值，该值由波浪频率和月池内流体活塞振荡固有频率构成的无量纲的Cf所决定。Cf值的表达式为：

式中：fw——波浪频率，Hz；

fh——月池内流体活塞振荡固有频率，Hz。

在浪流联合作用下，月池内流体受到的激励与波浪条件下较为类似。在浪流的扰动下，月池内流体在不同波浪周期下表现出不同的运动特性。借鉴波浪条件下的分析结论，认为来流为浪流的条件下，月池内流体的运动特性也由波浪频率和月池内流体活塞振荡固有频率构成的无量纲的Cf所决定。该值存在着临界值Cfe，当Cf＞Cfe时，月池内的流体表现出自激振荡的运动特性；当Cf＜Cfe时，月池内流体的振荡则表现出强迫振荡的运动特性。通过对试验结果的分析，月池的临界值Cfe介于0.71和1.42之间。

3 流体剪切层自持振荡频率及波浪遭遇频率预报

3.1 月池口流体剪切层自持振荡频率预报

在均匀流的条件下月池内流体所受的激励力主要来自于月池口的剪切层自持振荡，而剪切层在月池口的自持振荡现象类似于在月池口有一脉冲线声源的存在[5]。由于实船月池剪切层自持振荡产生的流噪声无法通过实验而得到其精确解，但噪声的频率可以利用相似定律从试验获得。根据试验得到的St数，可得到在均匀流条件下实船月池口流体剪切层的自持振荡频率，见表1。

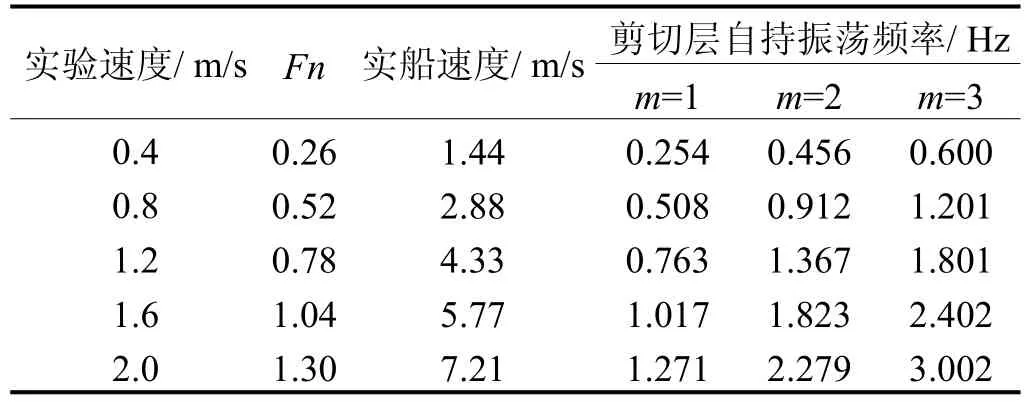
表1 均匀流条件下月池口流体剪切层的自持振荡频率

由表1可知，在实船的设计航速下，月池口流体剪切层自持振荡频率的范围为0.254～3.002Hz。

3.2 波浪遭遇频率预报

实船最高航行海况为4级，最大航速为15kn。国家海洋局根据我国沿海波浪统计分析，建议的波能谱公式为：

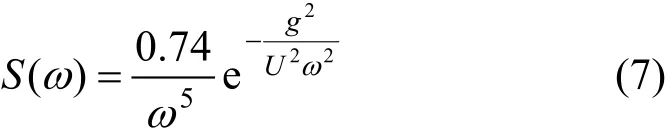
式中：ω——波浪圆频率，rad/s；

g=9.81m/s2；

U——风速，与1/3有义波高h1/3的关系为：该谱谱峰圆频率ωp与1/3有义波高h1/3的关系为：

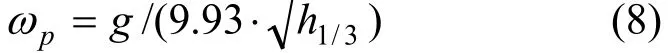
谱峰频率f与圆频率的关系为：f=ωp/ 2π，Hz。

该波能谱峰值频率所对应的能量占了整个波能谱能量的绝大部分，因此可由该峰值频率作为在该波高条件下的中心频率。实船航行海况下最大h1/3为2.5m，设本船在航行中可能遇到的h1/3分别为0.1m、1m、1.5m、2.5m，由此可得其中心频率见表2。

表2 不同浪级下的中心频率

由表2可知，在设计海况下，实船遇到的中心波浪频率范围为0.099～0.497Hz。

实船最大航速为15kn即7.5m/s左右，波浪遭遇频率fe的计算公式：

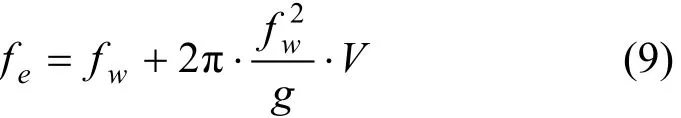
式中：fe——波浪遭遇频率，Hz；

fw——波浪频率，Hz；

V——航速，m/s。

根据式（9）计算得到波浪遭遇频率，见表3。

表3 波浪遭遇频率 Hz

由表3可知，该船航行时的波浪遭遇频率范围为 0.103～1.685Hz。

4 船底月池流激振荡特性分析

实船月池内流体活塞振荡固有频率为0.194Hz，首阶晃荡频率为0.447Hz。均匀流条件下实船月池口流体剪切层自持振荡频率范围为0.254～3.002Hz，高于月池内流体活塞振荡固有频率，但晃荡固有频率却在该范围之内，因此在月池口流体剪切层自持振荡的干扰下，月池内流体会有晃荡现象出现。

船舶在海上航行时往往伴随有波浪的出现，根据实船的设计海况要求，可得波浪频率范围为0.099～0.497Hz，波浪遭遇频率范围为 0.103～1.685Hz。该频率范围包含了月池内流体活塞振荡及晃荡的固有频率，因此在波浪及浪流联合作用的干扰下，月池内流体将有活塞振荡及晃荡现象出现。

由实船月池内流体活塞振荡频率的预报值及设计海况下波浪中心频率预报值，可得实船月池内流体振荡特性的无量纲值Cf的范围，见表4。

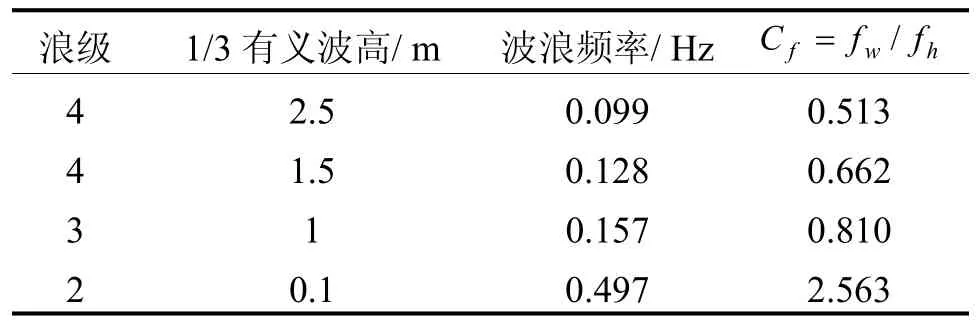
表4 无量纲值Cf

对试验结果的分析得到临界值Cfe的范围为0.71～1.42。从表4中可看出，在4级海况下，Cf值小于Cfe的下限，月池内流体的振荡以强迫振荡为主，即月池内流体以波浪或波浪遭遇频率振荡。在2级海况下，Cf值大于Cfe的上限，月池内流体的振荡以自激振荡为主，即月池内流体在波浪的扰动下将以活塞固有频率振荡。在3级海况下，得到的Cf值介于Cfe的上下限之间，所以此时月池内流体的振荡特性介于自激振荡与强迫振荡之间，即月池内流体除了在波浪或浪流的扰动下以波浪频率或遭遇频率振荡外，还将诱发其活塞固有频率的振荡。

5 结 语

本文开展了船底月池流激振荡特性研究，给出了船底月池内流体固有振荡频率计算公式。结合船底月池流激振荡试验，研究了船底月池在均匀流、波浪和浪流联合作用下的振荡特性。研究表明：均匀流条件下，在实船月池口流体剪切层自持振荡的干扰下，月池内流体会有晃荡现象出现；实船航行时，2级海况下，月池内流体的振荡以自激振荡为主；3级海况下，月池内流体的振荡特性介于自激振荡与强迫振荡之间；4级海况下，月池内流体的振荡以强迫振荡为主。本文的研究为实船的月池设计提供了理论和试验基础。

[1]金占礼，王宗利，李红云，刘正兴. 结构在无限流体域中振动时附连水质量的数值计算方法[J]. 上海交通大学学报， 2000, Vol.34 (8)∶ 1078-1082.

[2]朱仁庆，颜 开，吴有生. 盛液容器内液体二维晃荡的数值模拟[J]. 华东船舶工业学院学报， 1998, Vol.12(2)∶14-20.

[3]Chatellier L, Laumonier J & Gervais Y. Theoretical and experimental investigations of low Mach number turbulent cavity flows[J]. Experiments in Fluids, 2004, 36∶728-740.

[4]衣云峰，何祚镛. 水中圆柱腔流激振荡特性研究[J]. 中国造船. 1996, 37(3)∶ 36-47.

[5]Maisondieu.C, Le Boulluec.M Flow Dynamics in a Moon-pool Experimental and Numerical Assessment[A].Proceeding of the International Conference on Offshore Mechanics and Arctic Engineering[C]. Brazil∶ Rio de Janeiro, 2001. 401-409.