基于多基数系统的优化多标量乘快速算法

殷新春，张海灵，杨婷

(扬州大学 计算机科学与工程系，江苏 扬州 225009)

1 引言

自Koblitz和Miller[1]分别提出椭圆曲线密码体制(ECC, elliptic curve cryptography)以来，一直得到众多密码学家及密码学研究者的青睐。标量乘法，即已知域内整数k和椭圆曲线上一点P，求kP的运算。它是 ECC中最基本最耗时的运算，也是EC-DH、EC-NR、EC-DSA等协议的核心部分[2]。一些基于ECC的密码协议需要计算多标量乘，如ECDSA的验证部分需要计算kP+lQ，以及多重数字签名[3]等。

一种计算多标量乘的方法是分别计算m个标量乘kiPi的值，再对其进行求和，但这个方法效率不高。为了提高计算效率，较直接有效的方法就是改进标量的表示，如非邻接型(NAF)、联合稀疏型(JSF)及窗口法[1,4]等。双基数系统(DBNS, dou ble-base number system)由Dimitrov等人首先提出，随后研究者将其应用到多标量乘算法中[5～9]；2007年，文献[10]给出了5P的计算公式，设计实现了基于多基数链的单标量乘算法。

本文旨在解决 Dimitrov等在文献[6]Further Work中提出的实现kP+lQ + mR问题，采用多基数系统(MBNS, multi-base number system)表示标量，提出了快速的多标量乘算法。

2 相关知识

2.1 椭圆曲线

定义1 定义在域K上的Weierstrass方程：

所确定的平面曲线称为椭圆曲线；其中a1、a2、a3、a4、a6∈K，K为有限域。满足式(1)的(x,y)称为K域上的点；此外，椭圆曲线还定义一个特殊的无穷点O；即域K上的点集和一个无穷远点O组成域K上的椭圆曲线E。

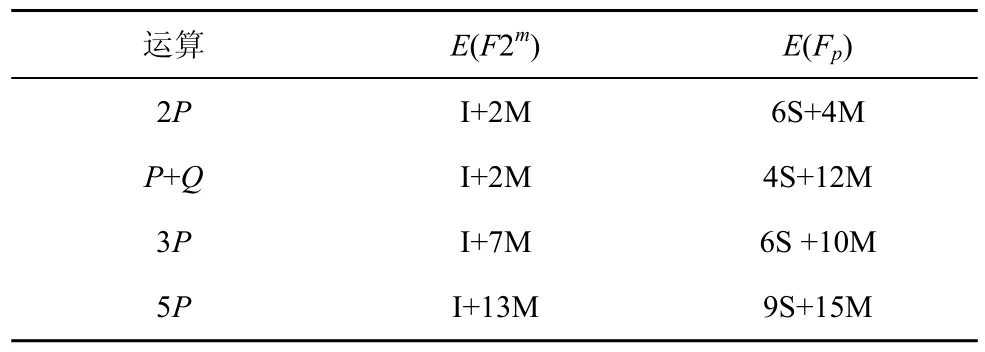
表1 点加、倍点计算开销

2.2 整数的多基数表示

设B= {b1,…,bl}是一个小整数的集合，则任何一个整数k都可以表示成的形式。本文主要研究的是B= {2, 3, 5}的情况，具体定义如下。

定义2 设集合B= {2, 3, 5}，则k可以表示成如下形式：

该形式即为整数的多基数表示。

当B= {2, 3}时，即为整数的双基数表示。DBNS是高冗余的，而且表示长度非常短；与DBNS相比，MBNS冗余度更高，表示长度也更短。如仅考虑si=1情况下，整数100的双基数表示共有402个，而它的多基数表示就有8 425个。bi、ti、qi的大小影响标量乘中2倍点、3倍点和5倍点运算的运算次数，而m−1为标量乘中点加的次数。一个160 bit的大整数如果使用双基数系统来表示需要大约 23项，而如果使用多基数系统则需要约 15项就可以了[10]，因此与使用双基数系统计算标量乘相比，使用多基数系统能够大大提高椭圆曲线标量乘法的计算效率。

通常采用贪婪算法将整数k转化为多基数表示，下面给出转换算法：

算法1：多基数转换贪婪算法

3 MBNS滑动窗口多点乘算法

传统多标量乘算法Shamir方法，是将tbit的标量kj(1≤j≤m)写成一个m×t的代表矩阵，再进行预计算和存储。本文用多基数表示标量kj，提出了MBNS滑动窗口同时多点乘算法。

3.1 MBNS滑动窗口同时多点乘算法

在MBNS滑动窗口同时多点乘算法中，tbit的标量kj被划分成为窗口宽度为w的个窗口。

首先，要加大对农业科技投入的力度，加强对农业科学研究的投入。注重农业技术的改造与创新，使各项技术能够因地制宜地发挥应有的作用，同时把自主开发和引进新技术相结合，提高安徽省的农业科技水平。

在新算法中，采用了从左向右的滑动窗口的技术，即处理完第i个窗口后，跳过连续的零位，取接下来的连续w位置入第i+ 1个窗口中。由于一个数的多基数表示长度决定了点加的次数，而对于不同的w值，小于2w的所有元素的多基数表示并不相同，即w值不同，其所需点加次数也不相同。表2给出了不同窗口宽度下的平均点加次数，记为aw。

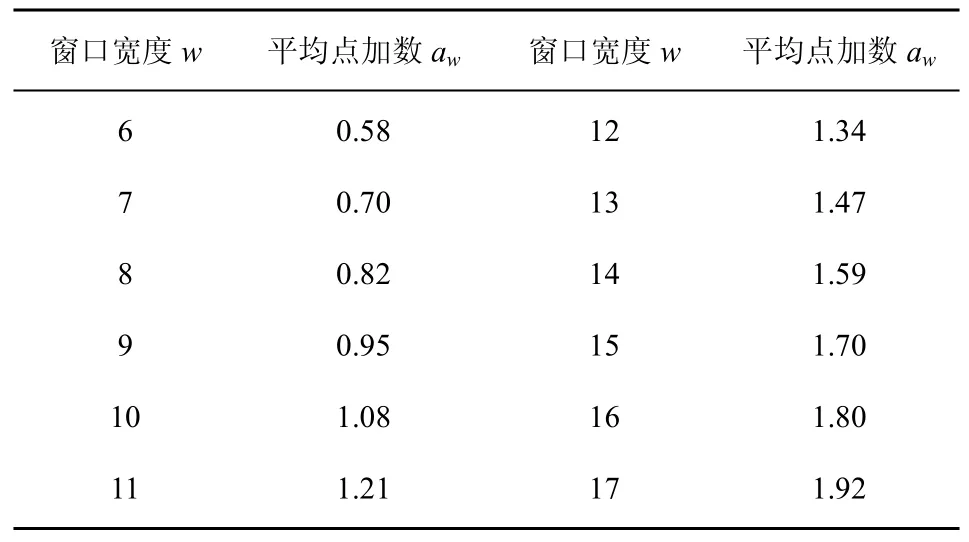
表2 窗口宽度w及其对应平均点加数

在这里假设P、Q、R已知，则算法为定点标量乘。对于这种标量乘法，其预计算表不需频繁更换，所以建立预计算表在整个椭圆曲线加密体制中所占比重不大，在这里主要讨论其赋值阶段的开销。由于算法采用了滑动窗口技术，实际计算窗口数小于d。

在算法赋值阶段，对每个窗口除需对其多基数表示计算点加外，即；还需分别对i(i= 3)个标量求和，即为。算法所需总的点加次数为：，赋值阶段算法总的开销近似为ADDw+ (d−1)wD，这里D为倍点运算。

3.2 交错MBNS滑动窗口同时多点乘算法

由于 NAF在标量的所有带符号表示中具有最少的非零位，因此如果对算法 2中的标量采用w-NAF编码，再对其进行处理，则具有更少的点加次数。

若使用w-NAF编码，则预计算阶段仅需计算小于2w−1的奇数项。例如，w取值为5，则只需计算−15到 15之间的奇数项。因而不同窗口宽度下的平均点加次数aw不同于算法2，具体见表 3。

表3 窗口宽度w及其对应平均点加数

由于宽度为w的NAF其平均非零数字的密度近似为，因而在赋值阶段，算法 3的点加次数为：，算法总开销近似为：ADDw+(d−1)wD。

4 算法分析

这节将分别比较传统Shamir算法、交错NAF方法、Sliding MBNS及I-MBNS。为了进行比较，各算法分别取不同的窗口宽度，具体为：Shamir算法取w=2、交错 NAF法取w∈{4,…,8}、Sliding MBNS 及 I-MBNS 取w∈{10,…,16}。

表4给出了算法在二进制域及素数域中，标量长度分别为160bit、192bit及230bit的性能分析。在二进制域中，求逆运算与乘法运算的效率比通常被认为是 8；而在素数域中，平方运算与乘法运算的效率比为0.8。

表4 算法性能分析

从表4中可以看出，二进制域上Sliding MBNS算法在t= 192bit时比 Shamir算法计算量减少了11%，比交错NAF方法减少了10%；I-MBNS算法计算量分别减少了 13%及 5%。素数域上 Sliding MBNS算法较之交错NAF方法效率并未得到很大改善，I-MBNS算法计算量减少了5%。

图1和图2分别显示了在二进制域及素数域标量长度t= 160bit时算法计算量与窗口宽度的具体变化情况。从图中可以看出，Sliding MBNS算法与I-MBNS算法的计算量均随着窗口宽度w的不断增长而逐渐减少。

图1 二进制域算法时间复杂度

图2 素数域算法时间复杂度

5 结束语

本文给出了结合文献[10]提出的 5倍点公式，提出了利用多基数系统计算椭圆曲线多标量乘的高效算法。需要强调的是，利用多基数系统计算椭圆曲线标量乘不仅能够提高标量乘的运算效率，使得基于椭圆曲线的密码体制实现更加便捷和高效，而且由于双基数系统表示的高度冗余性，多次计算同一个标量乘，计算过程可以完全不同，因此使用双基数系统计算椭圆曲线标量乘也可以抵抗某些边信道攻击[11,12]。

[1]HANKERSON D, MENEZES A J, VANSTONE S A.Guide to Ellip-tic Curve Cryptography[M].Springer-Verlag, 2003.

[2]刘铎, 戴一奇.计算椭圆曲线上多标量乘的快速算法[J].计算机学报, 2008, 31(7):1131-1137.LIU D, DAI Y Q.A new algorithm of elliptic curve multi-scalar multiplication[J].Chinese Journal of Computers, 2008, 31(7): 1131- 1137.

[3]CHEN T S, HUANG K H, CHUNG Y F.Digital multi-signature scheme based on the elliptic curve cryptosystem[J].Journal of Computer Science and Technology, 2004,19(4): 572-inside back cover.

[4]SOLINAS J.Low-weight binary representations for pairs of integers[R].Centre for Applied Cryptographic Research, University of Waterloo, Ontario, Canada: Technical Report CORR 2001-41, 2001.

[5]ADIKARI J, DIMITROV V, IMBERT L.Hybrid binary- ternary joint sparse form and its application in elliptic curve cryptography[EB/OL].http://eprint.iacr.org/2008/.

[6]ADIKARI J, DIMITROV V, MISHRA P.Fast multiple point multiplication on elliptic curves over prime and binary fields using the double-base number system[EB/OL].http://eprint.iac r.org/2008/.

[7]DOCHE C, KOHEL D R.Double-base number system for multi-scalar multiplications[EB/OL].http://eprint.iacr.org/2008/.

[8]LONGA P, GEBOTYS C.Fast multibase methods and other several optimizations for elliptic curve scalar multiplication[A].The 12th International Conference on Practice and Theory in Public Key Cryptography[C].Berlin: Springer, 2009.443-462.

[9]殷新春, 侯红祥, 谢立.基于双基数系统的快速标量乘算法[J].计算机科学.2008, 35(6): 186-189, 195.YIN X C, HOU H X, XIE L.Fast scalar multiplication based on DBNS[J].Computer Science, 2008, 35(6): 186-189.

[10]MISHRA P K, DIMITROV V S.Efficient quintuple formulas for elliptic curves and efficient scalar multiplication using multi-base number representation[EB/OL].http://eprint.iacr.org/2007.

[11]KOCHER C, JAFFE J, JN B.Differential power analysis[A].Proceedings of Advances in Cryptology[C].Berlin: Springer, 1999.388-397.

[12]郝艳华, 李磊, 王育民.利用多基链计算椭圆曲线标量乘的高效算法[J].电子科技大学学报.2008, 37(6): 868-871.HAO Y H, LI L, WANG Y M.Efficient scalar multiplication algorithm using multi-base chains[J].Journal of University of Electronic Science and Technology of China.2008, 37(6): 868-871.