土壤下渗问题的格子玻尔兹曼模拟
2010-07-11张东辉芮孝芳马哲树孔祥雷
张东辉,芮孝芳,马哲树,孔祥雷
(1.江苏科技大学船舶与海洋工程学院,江苏镇江 212003;2.河海大学水文水资源学院,江苏南京 210098)
应用连续介质模型来分析流体流动问题,实际上是通过分析微元体的质量守恒、动量定理、能量守恒推得N-S方程组,然后应用有限差分法等方法对微分方程进行离散,得到各结点的代数方程组进行求解.这类计算方法比较直观,目前应用非常广泛.但如果微分方程是强非线性的,数值稳定性便成为很大的问题,往往需要通过变换和设计特殊的数值格式来分析具体问题[1].
与上述思路不同,研究流体的流动也可从微观离散模型出发,即从更微观的尺度——大量分子运动的主控方程出发,向上“集成”来探讨流体流动特性[2],如图1所示.统计热力学中的玻尔兹曼方程[2]是描述系统中大量粒子分布函数f(x,v,t)的演化方程,它是联系微观与宏观的桥梁,其简化形式为


图1 两种推导宏观微分方程的途径Fig.1 Two kinds of processes deriving macroscopic differential equation
式中:e——微观粒子的速度,e=(ex,ey,ez);x——粒子的位置矢量,x=(x,y,z);F——作用在分子上的外力(也称源项);Ω(f*,f)——粒子与粒子之间的碰撞散射项,表示粒子分布函数f(x,e,t)由于粒子碰撞而发生的改变率.玻尔兹曼方程的解是不同时间的粒子分布函数f(x,e,t).一旦求得f(x,e,t)的具体表达式,可通过它与质量、速度、含水率等宏观量之间的关系,来推得后者的变化特点.
格子玻尔兹曼方法采用网格离散的方法求解玻尔兹曼方程[3].如果不考虑外力项的作用,式(1)在x处、α方向上可离散为[2]
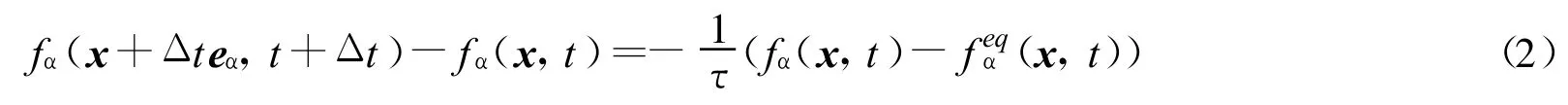
式中:eα——速度矢量;τ——弛豫系数;feqα(x,t)——平衡态分布函数.
由于土壤含水率与土水势(土壤水吸力)呈高度非线性关系,因而下渗方程通常是属于强非线性偏微分方程.对此问题的研究具有非常重要的意义,一方面可以了解水分或溶质在土壤中的运移和分布情况[4];另一方面也可从中深入分析产流的机理.目前下渗方程的求解主要是采用解析解法、有限差分法、有限元法和基尔霍夫变换法等[1],这些方法大多都存在计算精度、稳定性和计算效率之间的矛盾.应用格子玻尔兹曼方法来求解下渗方程是一种新的尝试,格子玻尔兹曼方法中蕴涵了多尺度展开的思想,而且具有编程简洁、边界易处理、易考虑粒子之间的相关作用等特点,因此它为复杂系统的模拟提供了新的途径,已成功应用于很多非线性问题的研究[5].格子玻尔兹曼方法应用于下渗问题的讨论有两类模型:第一类模型是建立在具体的土壤孔隙结构信息基础上,然后模拟其中的流动,这样可很好描述“孔隙尺度(pore scale)”层次上的流动[4-6].这种模型非常直观,但由于土壤孔隙结构的信息存储问题,对所研究问题的尺度是有限制的,很难将这种方法推广到大尺度下渗特性的研究.另一类模型是直接求解Richards方程,Ginzburg[7-8]发展出一种各向异性的格子玻尔兹曼模型(Lattice Boltzmann model,简称LB模型),对不同类型的土壤下渗过程进行了模拟,并考虑了水力传导率沿深度的变化,其模拟结果令人满意,但其过程非常晦涩,离真正实用推广还有一段距离;近些年,段雅丽等[9-10]提出了一种新的LB模型,成功求解了一定边界条件下的KDV方程(浅水波方程)、Sine-Gordon方程等,本文应用这种新的LB模型对下渗方程进行讨论分析.
1 物理模型
1.1 Richards下渗方程
土壤水流下渗过程可由Richards方程来描述:

这里所取的边界条件为

式中:K——水力传导率;D——水力扩散率;θ——土壤含水率;θ0——初始土壤含水率;θn——土壤表层含水率;t——下渗时间;z——土壤深度;L——土壤总深度.
如果水力传导率K、水力扩散率D与土壤含水率θ之间关系满足常用的Brooks-Corey公式时,即有:

式中 α和β是常数.方程(3)化为

其等价表达式为

当不考虑重力下渗的影响时,即水力传导率K=0时,上述方程即变为扩散方程:

Richards方程(3)只有在一些简化条件下才能获得分析解[1]:
a.当水力扩散率D为常数和水力传导率K=0时,方程(5)演变为线性扩散方程,当边界条件满足式(4)时,一定时间后不同深度的土壤含水率分布满足[1]:

erfc在数学上称为余误差函数.
b.当水力扩散率D为常数以及水力传导率K与土壤含水率θ呈线性关系时,方程(5)演变为线性Richards方程,相同的边界条件下,一定时间后不同深度的土壤含水率分布满足[1]:
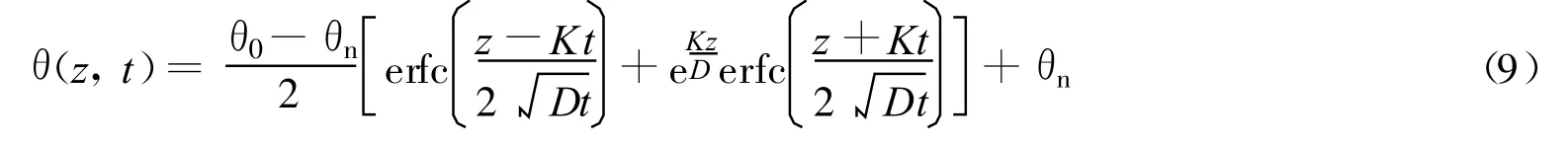
1.2 Richards方程的LB模型
本文所采用的格子玻尔兹曼模型对空间坐标并不进行多重尺度化处理,而对时间坐标引入3个时间尺度.对于一维LB模型网格,常用的是3速模型(α=0~2),如图2所示,每一网格结点上,存在3类不同速度的粒子,速度大小分别是-v,0,v.由于LB模型中的运动粒子在每一时间步长下都是移动单个的网格步长,C0定义为网格步长Δx与时间步长Δt之比,因而C0=v=Δx/Δt.
那么时间和空间坐标的多重尺度表达为

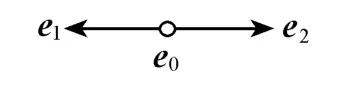
图2 3速模型示意图Fig.2 3-bit velocity model
空间坐标的微分形式不变,时间坐标的微分其多重尺度的形式为

粒子分布函数同样可展开为

对上式两边求和,根据质量守恒可得:

由此推得:

对离散方程(2)进行多重尺度处理,即可得到3个不同时间尺度的玻尔兹曼方程:

选择3速模型平衡态分布函数的各阶矩的形式为

为还原得到Richards方程,首先需对不同时间尺度的玻尔兹曼方程在不同方向上求和,然后将不同时间尺度对应的方程按不同数量级合并可得:

只要令B=1/(τ-0.5)ε,即可还原得到二阶精度的Richards方程(6),还原过程主要是保证宏观量选择和多尺度方案的正确性.
由于在计算中必须要知道平衡态分布函数,对于三速模型,3个方向的平衡态分布函数的求取可由式(15)确定.利用方程的对称性,可求得:

本文应用格子玻尔兹曼方法讨论下渗问题时,先从线性扩散方程和线性Richards方程开始,由于它们都存在分析解,这样一方面可验证LB模型的正确性,另一方面也可了解其误差特性.
2 格子玻尔兹曼方法的分析结果
如果仅考虑水力扩散效应,那么水分在土壤中的下渗过程由扩散方程(7)描述.如果水力扩散率D为常数,给定上边界含水率和初始土壤含水率,不同时间下不同深度的土壤含水率分布则呈余误差函数形式,即由式(8)决定.采用格子玻尔兹曼方法模拟扩散方程时,计算所取的参数为:初始土壤含水率 θ0=0.028,土壤表层含水率 θn=0.45,水力扩散率D分别为42.4cm2/min和424cm2/min.土壤总深度L=10m,网格结点数N=201,网格步长Δx=L/N=0.05m,时间步长Δt=0.01s,C0=Δx/Δt=5m/s,弛豫系数 τ=1.5.不同时间的土壤含水率分布如图3所示,LB模型的计算结果与分析解符合得非常好.水力扩散率越大,相同时间下深层土壤的含水率就越大.
图4是线性Richards方程的LB模型的计算结果,其水力扩散率D和水力传导率K与土壤含水率θ的关系是:D=42.4cm2/min,K=6θ cm/min.

图3 不同水力扩散率时水分在土壤中不同时间的分布Fig.3 Distribution of water in soils with different diffusion coefficients at different time

图4 线性 Richards方程的LB模型计算结果与分析解的比较Fig.4 Comparison between simulated results by LB model and analytical solutions of linear Richards equation
线性Richards方程考虑了重力下渗的影响,含水率在土壤中呈类似“S”形分布.其计算结果和真实土壤的含水率分布已经比较接近,在土壤上部存在“饱和带”,但湿润锋面并没有出现,这是线性Richards方程美中不足之处.
为了解各种因素的影响,可将格子玻尔兹曼方法的模拟结果与分析解进行比较,这里应用相对总体误差指标来衡量,其定义是:

图5(a)是线性扩散方程的LB模型的误差特性分析.对一定的扩散时间,存在一个最佳的弛豫系数τ,大约为1.0,此时计算误差最小,大约是0.1%.当弛豫系数增大或减小时(偏离最佳弛豫系数),计算误差几乎呈直线上升;在图5(a)中,上下两簇曲线分别代表不同的网格步长(时间步长均相同),这一结果表明:对应一定的时间步长,存在最佳的网格步长,即C0=Δx/Δt存在最优值.图5(b)是应用格子玻尔兹曼方法求解线性Richards方程的误差特性分析.这里仍然采用相对总体误差,它主要受到速度模型、边界格式、弛豫系数和格子长度等因素的制约.由于上下边界的含水率已经设定,边界节点各时段的分布函数用平衡态分布函数取定,所以没有讨论边界格式对计算误差的影响.
从图5(a)和图5(b)的比较可以发现:线性Richards方程的误差特性要更为复杂一些,其最佳弛豫系数随着下渗时间的延长,从1.0变为3.0,而且在本文计算的下渗时间范围内,随下渗时间的增大,最小计算误差是先增大后减小.对一定的下渗时间,存在一个最佳的弛豫系数,最小计算误差可达到0.1%.当下渗时间较短时,最佳弛豫系数在1.0附近;当下渗时间较长时,最佳弛豫系数是在3.0左右.这和大多数研究的结论不同,以往很多研究一般都认为弛豫系数范围在0.5~1.0,但本文通过对计算误差的分析,发现其最佳值有可能大于这一范围.当偏离最佳弛豫系数,计算误差几乎呈直线上升.
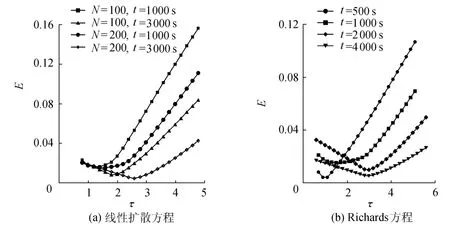
图5 LB模型误差特性分析Fig.5 Error analysis of LB model
为了了解真实土壤中的下渗情况,需直接求解非线性的Richards方程.这里采用了文献[1]中的算例,其中水力传导率K、水力扩散率D与土壤含水率θ及土壤饱和含水率θs之间的关系满足Brooks-Corey公式[1]:

Richards方程就变换为

LB模型宏观量取法如式(15)所示,其中m,n,α,β分别取:

土壤饱和含水率 θs=0.485,边界条件和初始条件仍然是:

Richards方程的分析解可由Philip提出的方法求出[1],Philips解的缺点是当下渗时间足够长时误差比较大.图6对LB模型的计算结果与Philips解[1]进行了比较.在下渗历时较短时,两者比较吻合;在一定的下渗时间后,则表现出一定的差别,由LB模型计算所得的湿润锋下渗速度要略大于Philip解[1]的结果,两者比较,最大计算误差大约是15%,土壤水分分布形态则基本一致.图7是下渗历时较长后,由LB模型计算所得的土壤水分分布特性.由图7所见,“饱和区”和“湿润锋”等典型的土壤下渗特征都可从中得到反映.这说明格子玻尔兹曼方法可以应用于实际土壤的下渗模拟研究.
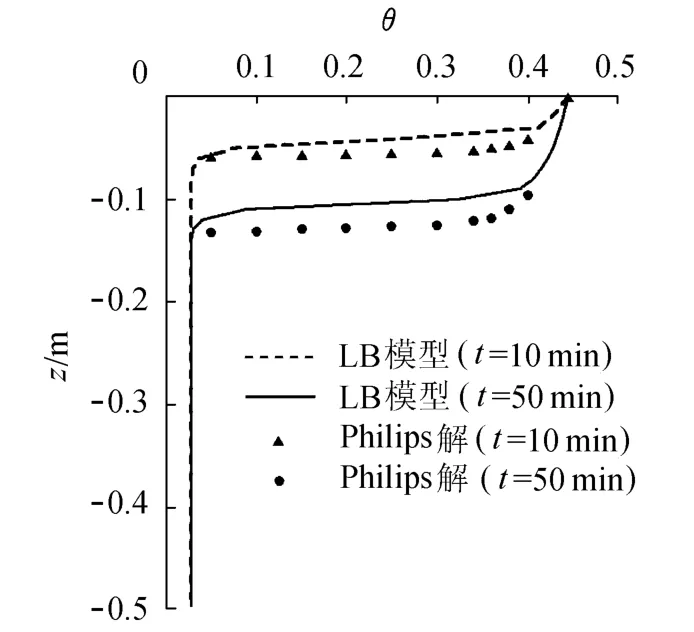
图6 LB模型计算结果与Philips解[1]的比较Fig.6 Comparison between simulated results by LB model and Philips solutions[1]

图7 非线性Richards方程LB模型的计算结果Fig.7 Simulated results by LB model for nonlinear Richards equation
由于Richards方程是属于流体力学的Burgers方程,而Burgers方程常被用于激波问题的模拟,激波现象最明显的特征是具有物理量梯度变化很大的前锋面.在土壤下渗问题中,也存在类似现象,比如说湿润峰(即干湿界面的前移)的存在.目前有些文献[11-12]就是讨论如何将激波传播的解的特性应用于Richards方程的求解.两者的区别在于:激波问题主要适用于超音速的可压缩流动,而Richards方程适用于下渗速度很慢的孔隙性介质流动.
3 结 语
与其他数值计算方法相比,本文采用的LB模型很好地解决了计算精度、稳定性和计算效率之间的矛盾,在下渗问题的应用上展现出可期待的前景.但研究中也发现:此LB模型需要水力扩散率与土壤含水率的函数关系可积,当土壤水分特征曲线满足Mualem-Van-Genuchten关系式时,水力扩散率与土壤含水率的函数关系表达式很难给出可积形式,对这一困难还需在未来研究中加以克服.
[1]雷志栋.土壤物理学[M].北京:科学出版社,1986:180-200.
[2]林宗涵.热力学与统计物理学[M].北京:北京大学出版社,2007:265-280.
[3]CHOPARD B.物理系统的元胞自动机模拟[M].北京:清华大学出版社,2003:20-78.
[4]VER MA N,SALEM K,MEWES D.Simulation of micro-and macro-transport in a packed bed of porous adsorbents by lattice Boltzmann method[J].Chemical Engineering Science,2007,62:3685-3698.
[5]YEOMANS J M,Mesoscale simulations:Lattice Boltzmann and particle algorithms[J].Physica A:Statistical and Theoretical Physics,2006,369:159-184.
[6]PAPAFOTIOU A,HELMIG R.From the pore scale to the lab scale:3-D lab experiment and numerical simulation of drainage in heterogeneous porousmedia[J].Advances in Water Resources,2008,31:1253-1268..
[7]GINZBURG I.Variably saturated flow described with the anisotropic Lattice Boltzmann methods[J].Computer&Fluids,2006,35:831-848.
[8]GINZBURG I.Lattice Boltzmann and analytical modeling of flow processes in anisotropic and heterogeneous stratified aquifers[J].Advances in Water Resources,2007,30:2202-2234.
[9]段雅丽.格子Boltzmann方法及其在流体动力学上的一些应用[D].合肥:中国科学技术大学,2007.
[10]ZHANG Jian-ying,YAN Guang-wu.Lattice Boltzmann method for one and two-dimensional Burgers Equation[J].Physica A:Statistical Mechanics and its Applications,2008,387(19):4771-4786
[11]CAPUTO J,STEPANYANTS Y.Front Solutions of Richards'Equation[J].Transport in PorousMedia,2008,74:1-20.
[12]MILLER C,ABHISHEK C,Farthing M.A Spatially and temporally adaptive solution of Richards'equation[J].Advances in Water Resources,2006,29:525-545.
