山区多沙水库干支流泥沙淤积数学模型及应用
2010-07-11舒彩文梅志宏谈广鸣
陈,舒彩文,武 见,梅志宏,谈广鸣
(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072;3.黄河勘测规划设计有限公司,河南郑州 450003;4.中国水电顾问集团昆明勘测设计研究院,云南昆明 650051)
我国西部地区水能资源丰富,大力开发水电资源实现西电东送,是我国西部大开发战略的重要组成部分.西部地区部分河流水土流失较为严重,含沙量较高,以元江为例,干流多年平均含沙量为3.5~4.3kg/m3,部分河段最大含沙量超过15kg/m3,在元江等多沙河道修建水库后泥沙问题将较为突出,因而预测建库后库区泥沙淤积对于工程的优化设计与运行具有重要的意义.目前预测水库泥沙淤积常采用一维水沙数学模型[1-5],国外比较有影响的一维模型有HEC-6模型[6]、FLUVIAL-12模型[7]、MIKE11模型[8]等,这些模型常用于低含沙冲积河流的冲淤计算,对于存在急流的山区多沙河流的冲淤计算不太适用.本文针对山区多沙河道水沙运动的特点,建立了适用于该类河流的一维非均匀非饱和输沙数学模型,将模型应用于元江上游戛洒江水电站库区泥沙淤积计算,计算结果可为水库设计与运行提供依据.
1 模型建立
1.1 基本方程
一维非均匀非饱和输沙数学模型的基本方程如下:
水流连续方程

水流运动方程
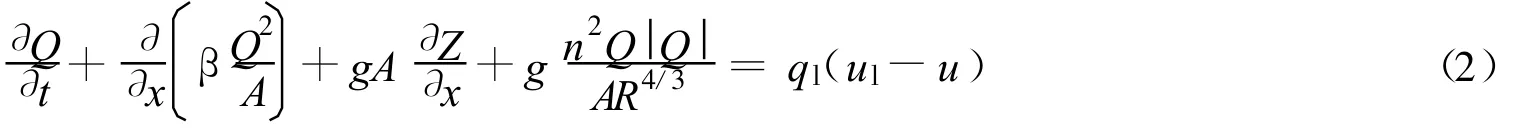
泥沙连续方程
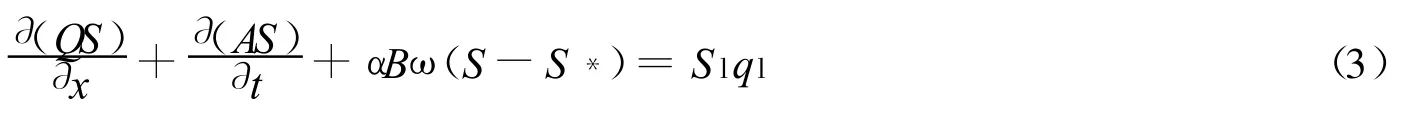
河床变形方程

式中:x——沿程距离;Q——流量;Z——水位;g——重力加速度;B——河宽;t——时间;ql,ul,Sl——侧向入流的单宽流量、流速和含沙量;A——过水断面面积;R——断面水力半径;β——动能修正系数;n——糙率系数;S——断面平均含沙量;S*——水流挟沙力;u——断面平均流速;ω——泥沙颗粒沉速;ρ——泥沙干密度;α——恢复饱和系数;Gb——推移质输沙率.
1.2 方程离散及求解
求解一维非恒定水流基本方程组采用有限体积法,此方法的特点是水量保持守恒.模型针对山区河道存在急流的特点,对运动方程的对流项采用一阶迎风格式进行离散,由于该格式求解非线性对流扩散方程时能获得相当高的精度[9],能够较好地模拟山区河道为急流时的水流运动,离散后的方程为
水流连续方程
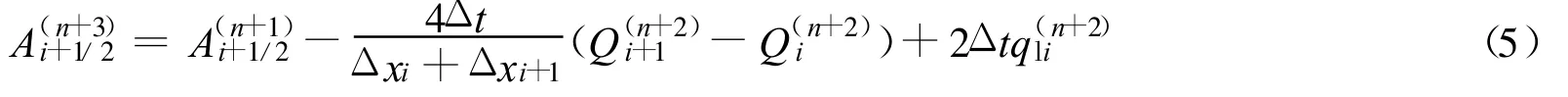
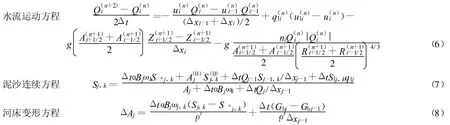
式中上角标为“0”的量表示上时刻的值.
1.3 补充方程
1.3.1 水流挟沙力公式
采用张瑞瑾水流挟沙力公式[10]:

分组水流挟沙力S*k采用窦国仁模式[11]:
其中

式中:S*——水流挟沙力;S*k——第k组沙水流挟沙力;K,M——水流挟沙力系数和指数;U——断面平均流速;——泥沙平均沉速;P*k,Pk——第k组沙水流挟沙力级配和悬沙级配;ωk——第k组沙对应的沉速;N——非均匀沙粒径组数;β——指数.
1.3.2 推移质输沙率
单宽推移质输沙率采用输沙经验关系式[12]:

其中

式中:vd——近底流速;d,d50——单组床沙粒径和非均匀沙中值粒径;h——平均水深.
1.4 支流入汇处理
考虑到支流入汇对干流的影响,方程(1),(2)和(3)均在等式右侧增加了侧向入流项的处理,而对于支流入汇后干流含沙量的计算,采用以下公式:

式中:Qm,Sm,Qc,Sc——干、支流入汇前上游最近断面的流量和含沙量;Q0,S0——入汇后首个干流断面的流量和含沙量.
2 模型应用
2.1 戛洒江水电站简介
戛洒江一级水电站位于元江干流上游戛洒江河段,坝址流域面积为1.81万km2,库区由上游石羊江段和支流绿汁江组成,干流石羊江库区平均比降约0.298%,支流绿汁江库区平均比降约0.3%,库区河道平面图见图1.大坝为面板堆石坝,最大坝高135 m,装机容量200MW.水库总库容14.79亿m3,有效库容为6.72亿m3,正常蓄水位为675m,死水位为660m.坝址处多年平均流量135m3/s,多年平均入库沙量为2840万t,多年平均含沙量为6.06kg/m3,历史最大含沙量超过18.0kg/m3.戛洒江具有径流小、含沙量高的特点.本文应用所建多沙水库干支流泥沙淤积数学模型,对戛洒江水电站的泥沙淤积问题进行研究.
2.2 计算范围及边界条件
2.2.1 计算范围与断面布置
计算范围包括干流石羊江长约60km河段(进口断面S1到坝址处),以及支流绿汁江长约50km河段(进口断面L1到支流入汇点),图1为水电站库区平面示意图.其中石羊江共布置47个断面,平均间距1.3km,支流绿汁江共布置41个断面,平均间距1.2km.
2.2.2 边界条件
模型进口边界条件为水库干支流进口断面的流量和含沙量值,出口边界为坝址处水位.由于模型进口断面处无水文站,其水沙过程通过坝址处元江水文站提供的水沙资料分配推算.其中,进口采用1988—1997年共10a的水文泥沙资料作为计算系列,年平均流量为121.94m3/s,年平均含沙量为7.09kg/m3,属于小水大沙的年份系列,入库悬沙中值粒径0.028mm.出口坝址正常蓄水位为675m,6—8月汛限水位为655m,9月汛限水位为665m.
模拟水库100a泥沙淤积过程时,选取1988—1997年的水沙系列为边界条件,前后连续计算10次共1200个月,模型计算时间步长为60s.
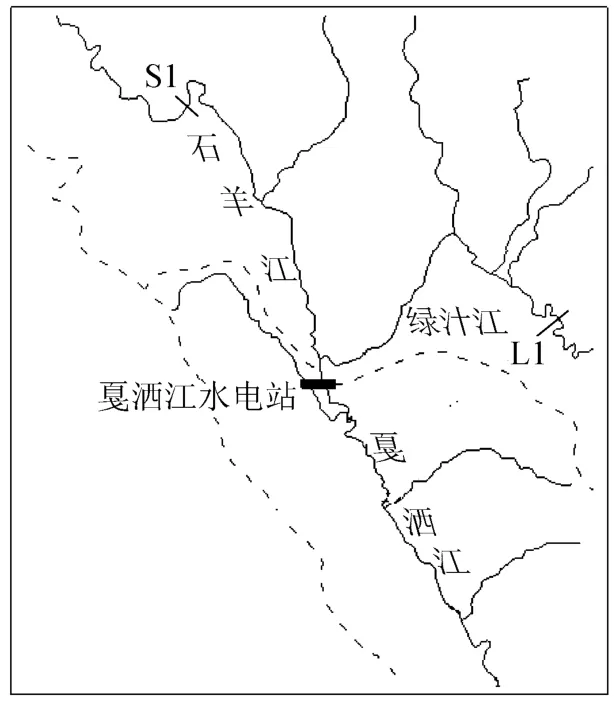
图1 戛洒江一级水电站库区示意图Fig.1 Reservoir area of Jiashajiang Hydropower Station
2.3 有关计算参数的选取
由于缺乏实测资料对模型挟沙力系数率定,采用平衡输沙的方法,假定河道建库前多年平均含沙量和水流挟沙力基本相等来确定系数.率定结果为:石羊江K平均值为0.93;绿汁江K平均值为1.16,M平均值为0.92.干支流糙率值通过实测水面线资料率定,糙率范围为0.035~0.060.恢复饱和系数 α在淤积时取为0.25,冲刷时取为1.0[13].
2.4 模型验证
图2为2006年6月25日至9月30日石羊江干流25号断面(坝上游33km)实测水位和模型计算值对比图,从图中可见两者最大误差不超过10cm,满足工程要求.由于缺乏水库泥沙冲淤验证资料,采用与戛洒江水电站相似的陡滩口水库泥沙淤积资料进行验证.图3为陡滩口水库淤积平衡后的沿程计算冲淤量与模型试验模拟冲淤量对比图,两者误差较小.所建一维非均匀非饱和输沙数学模型计算水库泥沙冲淤具有较好的精度.
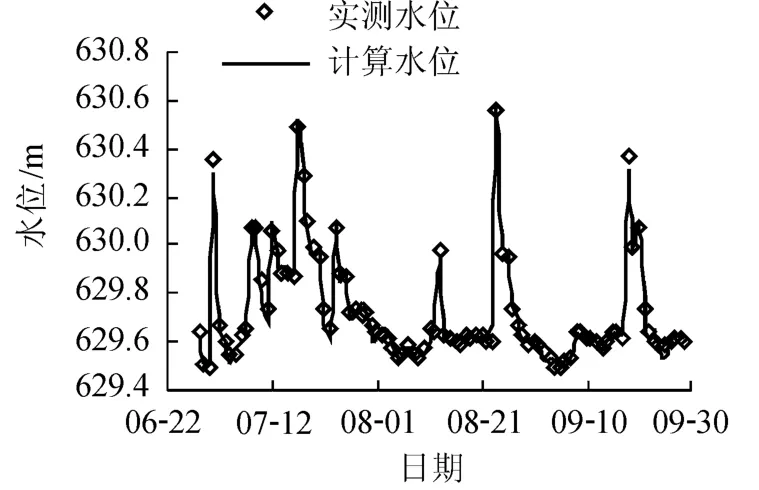
图2 水位实测与计算结果对比Fig.2 Comparison between observed and simulated water levels

图3 陡滩口水库沿程冲淤量验证Fig.3 Verification of deposition amount in Doutankou reservoir
2.5 水库淤积计算成果分析
2.5.1 河床纵横剖面变化
水电站运行100a期间,库区河道干流和支流河床纵剖面变化过程见图4.由图4可知,库区干支流泥沙均呈现三角洲淤积形态,三角洲淤积顶点随着水库运行年限的增加逐渐向坝前推移,但淤积速度逐渐变缓.由于干流库区泥沙淤积速度大于支流库区,当水库运行40 a后,干流库区泥沙淤积到支流入汇口附近,干流部分泥沙进入支流绿汁江库区发生淤积,使得绿汁江淤积加快,支流库区在运行80a后达到冲淤平衡.
2.5.2 水库库区泥沙淤积及排沙比分析
表1为戛洒江库区干流、支流及整个库区泥沙累积淤积总量及排沙比计算结果.由表1可见,在计算年限100a内,水库一直处于淤积状态,干流库区运行100a后未达到冲淤平衡,总淤积量为13.75亿t,排沙比达到85.78%,支流库区运行80a后达到冲淤平衡,总淤积量为8.8亿t,排沙比达到100%.
2.5.3 库容变化
水库初始运行时正常蓄水位675m,水库总库容、死库容和有效库容分别为14.79亿m3、8.07亿m3和6.72亿m3.水库运行后泥沙淤积导致库容损失,表2为戛洒江一级电站运行后库容变化情况及库容损失率情况.从表2可以看出,水库泥沙不断发生淤积,库容损失不断增加.水库运行40a后,死库容损失率接近50%,运行至100a,死库容损失率达到100%,有效库容损失率为6.53%,总库容损失率为57.53%.
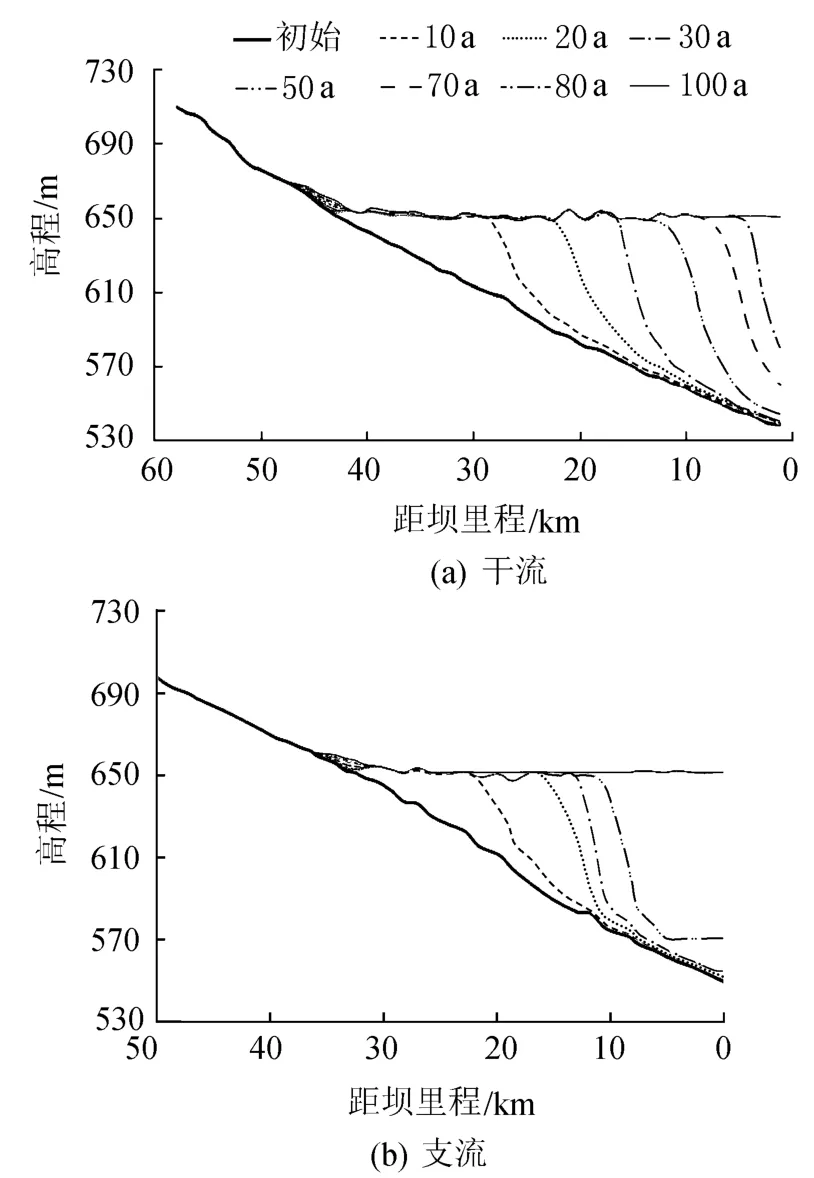
图4 库区河道深泓线变化Fig.4 Evolution of talweg in reservoir area
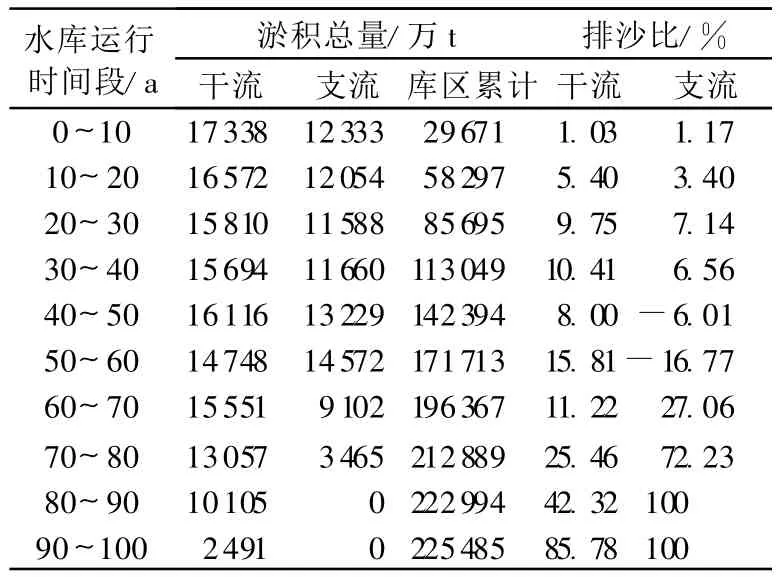
表1 戛洒江库区泥沙累积淤积总量及排沙比计算结果Table 1 Simulated results of total sediment deposition amount and delivery rate in Jiashajiang reservoir area
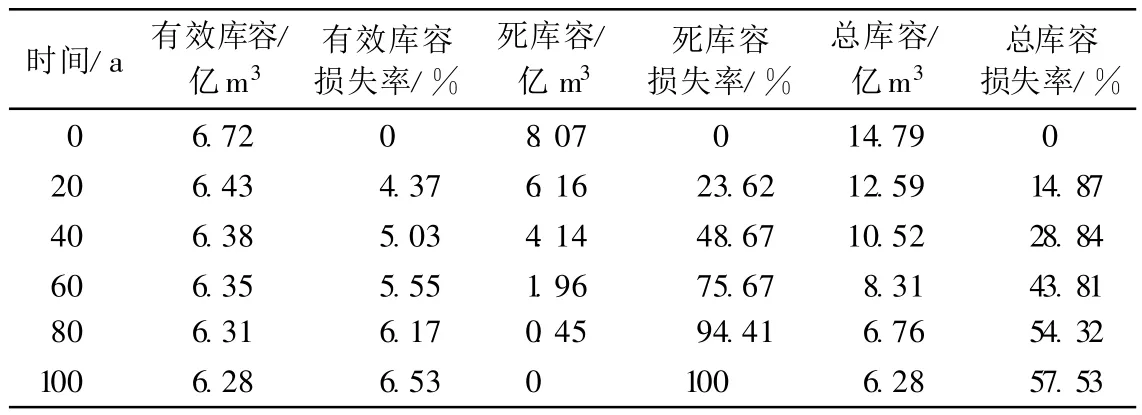
表2 建库后戛洒江水库库容损失特征值Table 2 Values of loss rate of storage in Jiasajiang reservoir
3 结 论
针对我国西南部山区多沙河流水沙运动的特点,建立了一维非恒定非饱和输沙数学模型用于水库泥沙淤积预测,模型对运动方程对流项采用一阶迎风格式进行离散,使得模型能够对山区河道急流流态进行模拟.最后将模型用于元江上游戛洒江水电站库区泥沙淤积计算,结果表明:干支流库区均呈三角洲淤积形态,三角洲淤积顶点随运行年限的增加逐渐向坝前推移,但淤积速度逐渐变缓.干流库区运行100a后未达到冲淤平衡,支流库区运行80a后达到冲淤平衡.干流库区运行100a后总淤积量为13.75亿t,排沙比达到85.78%,支流库区运行80a后总淤积量为8.8亿t,排沙比达到100%.水库运行100a后,干支流累计有效库容损失率为6.53%,死库容损失率为100%,总库容损失率为57.53%.
[1]汤立群,陈界仁,陈国祥,等.白沙水库一维泥沙数学模型及电厂取水方案计算[J].河海大学学报,1998,26(5):34-38.(TANG Li-qun,CHEN Jie-ren,CHEN Guo-xiang,et al.One dimensional model of reservoir sedimentation and its application incalculation for water intake of a power plant[J].Journal of Hohai University,1998,26(5):34-38.(in Chinese))
[2]杨国录,吴卫民,陈振虹,等.SUSBED-1动床恒定非均匀全沙模型[J].水利学报,1994(4):1-10.(YANG Guo-lu,WU Weiming,CHEN Zhen-hong,et al.SUSBED-1 movable bed modeling of graded sediments[J].Journal of Hydraulic Engineering,1994(4):1-10.(in Chinese))
[3]张小峰,谢葆玲,许全喜.三峡水库蓄水初期泥沙淤积预测模型研究[C]//中国水力发电工程学会水文泥沙专业委员会第六届学术讨论会论文集.成都:时代出版社,2005.
[4]黄仁勇,黄悦.三峡水库干支流河道一维非恒定水沙数学模型初步研究[J].长江科学院院报,2009,26(2):9-13.(HUANG Ren-yong,HUANG Yue.Preliminary study on 1-D numerical simulation of unsteady flow and sediment transport in mainstream and tributaries of three gorges reservoir area[J].Journal of Yangtze River Scientific Research Institute,2009,26(2):9-13.(in Chinese))
[5]黄永健,谈广鸣,吕平,等.黏性泥沙数学模拟中几个关键问题的研究进展[J].水利水电科技进展,2009,29(3):90-93.(HUANG Yong-jian,TAN Guang-ming,LV Ping,et al.Research advancesof severalkey problems in the numerical simulation of cohesive sediment[J].Advances in Science and Technology of Water Resources,2009,29(3):90-93.(in Chinese))
[6]FELDMAN A D.HEC models for water resources system simulation:theory and experience[J].Advances in Hydroscience,1981(12):297-423.
[7]CHANG H H,HANISON L L,LEE W,et al.Numerical modeling for sediment-pass-through reservoirs[J].Journal of Hydraulic Engineer,ASCE,1996,122(7):381-388.
[8]王领元.应用MIKE对河流一、二维的数值模拟[D].大连:大连理工大学,2007.
[9]张小峰,中川一,许全喜.一阶迎风差分格式的精度问题[J].武汉大学学报:工学版,2001,34(1):6-10.(ZHANG Xiao-feng,NAKAGAWA H,XU Quan-xi.On accuracy of first order upwind scheme[J].Journal of Wuhan University of Hydraulic and Electric Engineering,2001,34(1):6-10.(in Chinese))
[10]张瑞瑾.河流泥沙动力学[M].北京:中国水利水电出版社,1989.
[11]窦国仁,赵士清,黄亦芬.河道二维全沙数学模型研究[J].水利水运工程学报,1987(2):1-12.(DOU Guo-ren,ZHAO Shi-qing,HUANG Yi-fen.Study on two-dimensional total sediment transport mathematic model[J].Hydro-Science and Engineering,1987(2):1-12.(in Chinese))
[12]国务院三峡工程建设委员会办公室泥沙专家组.长江三峡泥沙问题研究:第五卷:1996—2000[M].北京:知识产权出版社,2002.
[13]韩其为.水库淤积[M].北京:科学出版社,2003.
