考虑水质的水资源调配模型及其解法

张松达,苏 飞,夏梦河

(1.宁波原水集团有限公司,浙江宁波 315900;2.浙江省水利河口研究院,浙江杭州 310020;3.余姚市水利局,浙江 余姚 315400)

水资源是基础性的自然资源和公共性的社会资源.随着城市化进程的加快,对水资源数量和质量的承载要求会越来越高,水量水质的联合调配作用也会显得越来越重要.尤其对水资源短缺和水质污染相对严重的地区来说,在统一考虑水量和水质问题的前提下进行水资源差别调度,具有重要的实际意义.

地处浙东沿海的宁波市,水资源总量不足,人均水资源量仅1285m3,远低于全国和全省的平均水平,并且该市城市化水平较高,经济和社会保持持续、稳定、快速发展,工业及居民生活用水量不断提高,水资源供求矛盾十分突出.为了切实解决好水资源问题,充分利用河网径流,改善居民用水水质,宁波市在水资源配置上形成了以分质供水、优水优用、挖潜增量、改善水质为主要内容,按水质配置水量的调配模式.

水库群及河网作为沿海地区较为普遍的水资源系统,水库水往往作为优质水主要供给生活和重要工业,而河网水作为农业、一般工业和环境用水水源.近年来,以大系统理论为基础的水库群联合调度方法已在宁波地区逐步得到实施[1],但水库群-河网水量水质联合调配问题还没有得到解决.为此,笔者以余姚地区为例,在水库群联合调度的大系统分解-协调模型的基础上,综合考虑河网环境需水和供水水质的不同要求,建立了水库群 河网水资源联合调配模型,并研究了其有效解法.

1 水库群-河网联合调配模型

1.1 河网环境需水量计算模型

余姚地区为感潮平原河网地区,河流众多,水系密布.由于受潮水、农业灌溉和部分工业取水的影响,该地区河流水动力情况要比一般河流复杂得多.同时,生活、工业废污水排放和灌溉回归水不断进入河网,增加了河网水质问题的复杂性.姚江干流源头属Ⅰ类水;四明湖水库坝下至城区属Ⅱ～Ⅲ类水;城区内河属Ⅲ～Ⅳ类水;市区3个节制闸至丈亭属Ⅲ～Ⅳ类水,至姚江水闸属Ⅱ～Ⅲ类水,部分河段水质已不能满足水功能区要求,水量水质联合调配时必须考虑水流水质的这种变化规律.

1.1.1 水流控制方程

水流数值计算采用圣维南基本方程组[2-5]

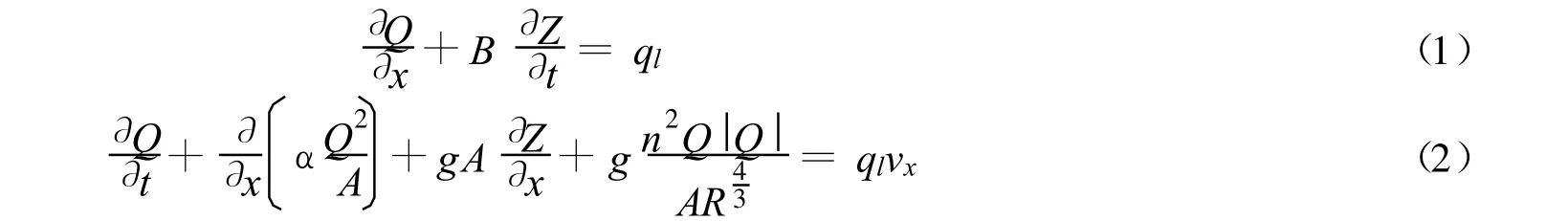
式中:Q——流量;Z——水位;B ——水面宽;A——过水断面面积;ql——单位河长旁侧入流流量;α——动量校正系数;n——河床糙率系数;R——水力半径;vx——旁侧入流沿水流方向的速度分量,如果旁侧入流垂直于主流,则 vx=0;g——重力加速度.

1.1.2 水质控制方程

水质模型采用考虑污染物对流、扩散与线性降解的基本方程[6-7]

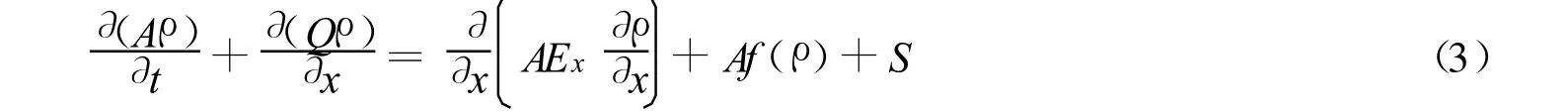
式中:ρ——断面污染物质量浓度;Ex——扩散系数;f(ρ)——污染物降解参数;S——源汇项.

1.1.3 连接方程和边界方程

连接方程将汊点作为具有水量和污染物浓度调节作用的贮水池.边界条件中的外边界水流主要由闸门控制,内边界主要为点源排放、集中取水等方式.通过河道内闸、堰调节各河区的水量,以满足不同用水的需要.水流水质计算同时满足水流连续性和污染物质量守恒2个条件.

1.1.4 迎风差分格式

对于非稳态河网来说,水流计算是非常重要的.考虑到流向的不定性,水流计算采用四点加权隐格式[8-9],将河道方程、边界方程等进行离散,形成水流连续性和动量方程组

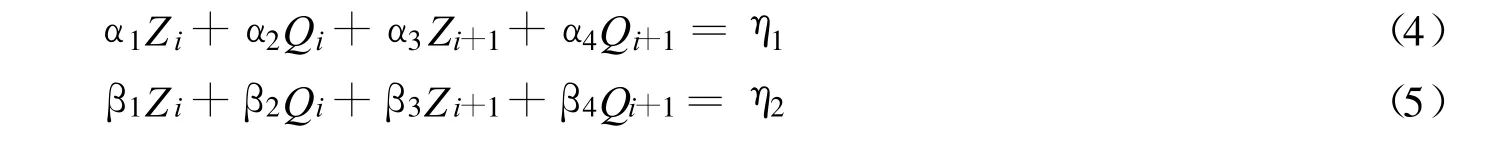
式中 αi,βi,ηj(i=1,2,3,4;j=1,2)为方程系数.

水质计算采用迎风差分格式.同向流(包括顺流和逆流,即水流沿河道向同一方向流动.河网水流在引水冲污、汛期排涝时多为这种流态)差分方程为

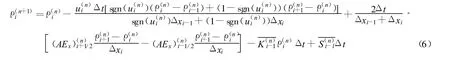
异向流(包括对向流和背向流,即水流在当前断面河道向相反方向流动.枯水期取水灌溉、污水集中排放以及受潮位涨落影响的河流多为这种流态)差分方程为

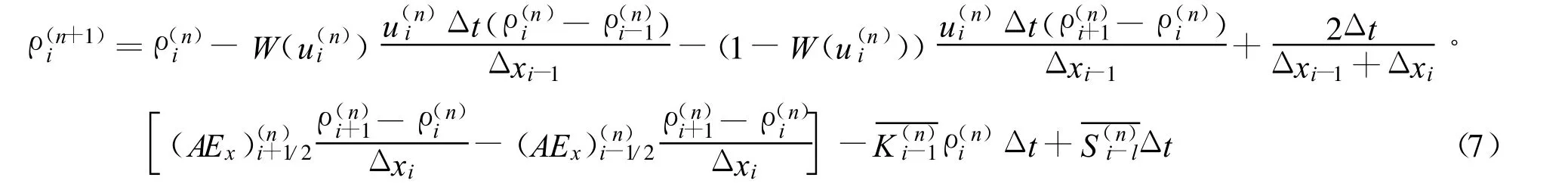
式中:u——断面流速;W——水动力调节因子;K——污染物河段衰减系数;sgn——符号函数.

1.2 水库群联合优化调度模型

根据余姚水库群系统的网络关系,建立水资源系统优化调度模型[10].该模型是一个多层次大系统模型,具有2层谱系结构,第1层为模拟模型,第2层为线性规划模型.水库群系统的协调变量为各水库的供水量,协调变量应满足总系统供水能力约束.各子系统根据总系统下达的协调变量反馈相应的目标函数值(弃水量和缺水量).总体协调层模型为

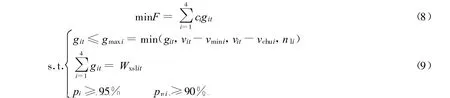
子系统模型为

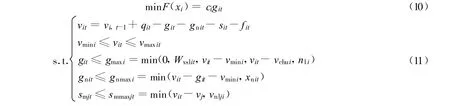
式中:git——i子系统t时段水厂供水量;ci——价格系数,i子系统水厂单位供水量产生的弃水量;gmaxi——i子系统水厂最大供水能力;vit,vi,t-1——i子系统t时段和t-1时段水库库容;vmini——i子系统死库容;vmaxit——i子系统t时段允许蓄水库容;vchui—— i子系统水厂取水口高程相应库容;nli——i水库管网输水能力;Wxslit——i子系统t时段水厂需水量;pi——i子系统生活供水保证率;pni——i子系统农业供水保证率;qit——i子系统t时段水库来水量;gnit——i子系统t时段农业供水量;sit——i子系统t时段水库蒸发渗漏损失量;fit——i子系统t时段水库弃水量;xnit——i子系统t时段农业需水量;smjt——j连接工程t时段输水能力;smmaxjt——j连接工程t时段最大输水能力,j=1为四明湖至牟山湖的连接工程,j=2为陆埠至梁辉的连接工程;vj——j连接工程出水口对应库容,j=1为四明湖出水口,j=2为陆埠水库出水口;vnlji——i子系统j连接工程管网输水能力.

1.3 水库群-河网联合调配模型

由水库群以及河网共同组成的供水系统,水库主要向生活、重要产业用户供水,河网则向农业、一般产业、生态环境用户供水.水库群可以通过有关输水设施调水,河网之间也可通过闸泵工程调水,同时,水库还可向河网补水.整个系统蓄水、供水、用水之间,水库群和河网之间,各水库群之间,各河网之间存在着耦合关系.

针对该系统特点,建立3级结构的水库-河网对偶系统模型.即将整体系统分解为河网和水库群2个分系统.其中河网分系统按水级分解为若干个更低一级的子系统;水库群分系统也相应地分解为若干个更低一级的子系统.

2 模型求解

2.1 河网水流水质模型求解

对于非稳态河网水质计算问题,由于形成的方程组多为稀疏矩阵,需要研制相应的解法[11].实际应用中出于规划分析等需要,经常采用较为简便的方法.本文从实用角度出发,在主要考虑河道异向流的情况下,利用流量对水质浓度计算的权重影响,进行非稳态河网水质的校正计算分析,并进行了验证.

上述模型,采用牛顿迭代法和压缩存储的高斯列主元消去法进行求解[12],水流计算中引入衰减二乘自回归校正技术,水质计算中引入流量调节因子.水流水质模型的验证结果和实际应用表明,所建立的模型能够较好地反映地区河网的水质变化情况.

2.2 水库群联合优化调度模型求解

各子系统根据总系统下达的协调变量反馈相应的目标函数值(弃水量和缺水量).当水库群系统的弃水量和缺水量达到最小时,则输出相应的结果[13-14];当总系统内各子系统在当前协调变量下都达到各自供水保证率要求时,则增加总系统供水能力,同时求得各子系统的供水量,再次进行子系统模拟计算直至总系统弃水量和缺水量最小.对于上层大系统给定的供水量建立模拟模型,模拟子系统的运行状况以得出各子系统的弃水量和缺水量.

当子系统内有多个供水工程能同时满足某一用水户需水时,如陆埠和梁辉水库均可以供水至姚中区,从满足水资源需求量的角度来说,无论哪个水库供水至水厂,再进入供水管网,只要总量满足即可.但是,对于子系统的目标函数(即缺水量、弃水量均为最小),由于不同水库当前蓄水情况不同、集雨面积下时段的来水量不同,则存在优先使用哪个水库的水资源问题.为确定优先顺序,引进动态空库系数控制变量[10],变量值越小表明面临时段产生弃水的可能性越大,应优先取用该水库的水资源.

2.3 水库群-河网联合调配模型求解

将余姚市水资源系统分为水库群和河网2个分系统.水库群(河网)分系统进一步划分为姚东水库群(河网)、姚中水库群(河网)、姚北水库群(河网)几个子系统.子系统采用动态空库系数的模拟方法,分系统采用线性规划方法,2个分系统通过反馈进行协调,用迭代法进行求解.2个2级分系统是一个相互耦合的对偶系统,把2级河网分系统的缺水量反馈给2级水库群分系统,将其加到这一分系统的供水量的约束条件中,相应于2级水库群分系统,将弃水量反馈给2级河网分系统,作为这一分系统的来水.

当前后2次水库群2级分系统的弃水量之差,或者当前后2次河网2级分系统的缺水量之差小于允许误差时,便求得了系统平衡解.据此,采用0.618法调整需水量约束条件,重复计算,通过对偶迭代可以求得系统最大平衡解,即模型最小弃水量(最大可供水量)目标.

2.4 结果分析

采用大系统分解-协调对偶迭代技术对水库-河网系统模型进行的优化调度结果表明:余姚市可供水量由原来3.93亿m3提高到4.54亿m3,增加供水6 100万m3,增加比例 15.5%;水库群供水能力由原来52.6万t/d增加到59.7万t/d,增加7.1万t/d,增加了13.5%;河网供水增加1700万m3,增加4.3%,充分利用了河网径流,能满足河网各类水质目标要求,河网环境需水6600万～8000万m3/a;水库群-河网的联合优化配置,使得中长期水资源的水量和水质能够支持社会经济的可持续发展.

3 结 语

在水资源优化配置和调度中,考虑地区水环境保护和改善要求,建立水质水量的联合调配模型,是水资源研究领域的热点和难点.为了解决感潮平原河网地区水库群-河网水资源联合调配问题,笔者以余姚地区为例,在水库群联合调度大系统分解-协调模型的基础上,综合考虑河网环境需水和供水水质的不同要求,建立了水库群 河网水资源联合调配模型,并研究了其有效解法.应用结果表明,采用本文所述联合调配模型和求解方法,可以将水量配置与水质配置相结合,实现感潮平原河网地区水量水质的联合调配,为河网水质的实时管理和调控提供决策依据,提升水资源的综合利用和管理层次.

[1]余姚市水利局.余姚市水资源优化调度决策支持系统技术研究报告[R].余姚:余姚市水利局,2008.

[2]李曦,逄勇.江阴城区水环境数学模型建立及应用[J].水资源保护,2009,25(2):38-41.(LI Xi,PANG Yong.Application of water environment numerical model in Jiangyin City[J].Water Resources Protection,2009,25(2):38-41.(in Chinese))

[3]张聃,周蔚,徐海岚,等.引配水对京杭运河杭州段水质的改善预测[J].水资源保护,2010,26(3):45-48.(ZHANG Dan,ZHOU Wei,XU Hai-lan,et al.Prediction of water quality improvement of Grand Canal(Hangzhou section)by water diversion[J].Water Resources Protection,2010,26(3):45-48.(in Chinese))

[4]刘中峰,李然,陈明千,等.大型水库三维水质模型研究[J].水利水电科技进展,2010,30(2):5-9.(LIU Zhong-feng,LI Ran,CHENMing-qian,et al.Three-dimensional model for water quality of large reservoirs[J].Advances in Science and Technology of Water Resources,2010,30(2):5-9.(in Chinese))

[5]孙志林,陈永明,夏珊珊,等.基于混合模型的河网输水能力计算[J].河海大学学报:自然科学版,2010,38(2):144-148.(SUNZhi-lin,CHEN Yong-ming,XIA Shan-shan,et al.Calculation of water transport capacity of river networks based on mixed models[J].Journal of Hohai University:Natural Sciences,2010,38(2):144-148.(in Chinese))

[7]许其功,刘鸿亮,沈珍瑶.有限单元算法在水质模拟中的应用研究[J].环境科学与技术,2006,29(9):11-13.(XU Qi-gong,LIUHong-liang,SHENZhen-yao.Application study of FEM in water quality simulation[J].Environmental Science and Technology,2006(9):11-13.(in Chinese))

[8]郑孝宇,褚君达,朱维斌.河网非稳态水环境容量研究[J].水科学进展,1997,8(1):25-31.(ZHENGXiao-yu,CHU Jun-da,ZHU Wei-bin.A study on unsteady water environmental capacity of river network[J].Advances in Water Science,1997(1):25-31.(in Chinese))

[9]卢士强,徐祖信,罗海林,等.上海市主要河流调水方案的水质影响分析[J].河海大学学报:自然科学版,2006,34(1):32-36.(LU Shi-qiang,XU Zu-xin,LUO Hai-lin,et al.Influence of water diversion schemes on water quality of Shanghai river network[J].Journal of Hohai University:Natural Sciences,2006,34(1):32-36.(in Chinese))

[10]夏梦河,姚俊杰,奕永庆.余姚市水资源优化配置与调度的大系统模型及其解法[J].浙江水利科技,2008(1):18-20.(XIA Meng-he,YAO Jun-jie,YI Yong-qing.Large system model for optimal allocation of water resourcesin Yuyao and its solution[J].Zhejiang Hydrotechnics,2008(1):18-20.(in Chinese))

[11]陈杨,俞国青.明满流过渡及跨临界流一维数值模拟[J].水利水电科技进展,2010,30(1):80-84.(CHEN Yang,YU Guo-qing.One-dimensional numerical simulation of transcritical flows and transition between free surface and pressurized flows[J].Advances in Science and Technology of Water Resources,2010,30(1):80-84.(in Chinese))

[12]郑权.牛顿迭代法在弱条件下的二阶收敛性和比值收敛因子[J].北方工业大学学报,2003,15(1):126-129.(ZHENG Quan.Quadratic convergence and convergence ratio factor of Newton's iteration method under weak conditions[J].Journal of North China University of Technology,2003,15(1):126-129.(in Chinese))

[13]韩帅,夏自强,刘猛,等.水库调度对大坝下游河道生态径流的影响[J].水资源保护,2010,26(1):21-23.(HANShuai,XIA Ziqiang,LIUMeng,et al.The influence of reservoir operation on in-stream ecological flow downstream of dam[J].Water Resources Protection,2010,26(1):21-23.(in Chinese))

[14]朱记伟,张洪波,辛琛,等.水库调度PSO优化模型及求解方法[J].系统工程,2010(1):105-112.(ZHU Ji-wei,ZHANG Hongbo,XIN Chen,et al.PSO model and calculation method to reservoir optimal operation[J].Systems Engineering,2010(1):105-112.(in Chinese))