三角网格曲面的球面参数化
2010-07-07姚建强何援军
姚建强, 何援军
(上海交通大学计算机系,上海 200240)
3D几何模型的发展,使网络曲面的参数化成为近年来图形学的研究热点之一。由于三角网络曲面具有简单,灵活以及受各种图形硬件的广泛支持的特点[1],三角网格曲面的参数化在娱乐业、制造业、医学和科学可视化等领域中得到广泛的应用。
三角网格曲面参数化主要是将由三角网格M表示的曲面S与二维流形参数域之间寻求一个一一对应映射ϕ 使得ϕ (M)与M同构,并使曲面映射后扭曲失真最小。过去的一段时间里,许多学者一直在研究如何计算扭曲失真的程度。并提出了等积映射、调和映射、保角映射、虚拟边界等方法来减小失真[2]。
1 前人工作
三角网格曲面的参数化主要分为曲面网格参数化和网格内部点映射。
1.1 三角网络参数化
根据参数域的不同,三角网格参数化方法主要可以分为平面参数化和球面参数化。
平面参数化是目前研究得最多的参数化算法,它把一个空间三角网格尽可能均匀地摊平到某个平面区域中。Tutte[2]在1960提出了凸组合方法, Floater[3-4]在Tutte的基础上通过给每条边附加一个与边长相关的权值改进了凸组合方法。它们的基本思想是固定边界点,内部点由它的相邻点的加权凸组合给出。并提出了保角参数化和均值参数化方法。
通常几何模型都是由亏格为零的封闭网格组成,如变形的球体。对于这样的模型,将它参数化到它拓扑同构的球面更为合理[5]。近些年,人们逐渐把球面参数化作为研究的重点。
一个最简单的方法就是先使用一个三角形作为边界将三角网络参数化到平面上,然后将平面域映射到球面上。这种方法在实践中使用得很好,但在理论上没有什么保证,并且结果会依赖于三角形边界的选取[6]。Shapiro等[7]提出了一个基于网格简化的球面参数化方法,该方法先将原始网格简化为四面体,再把这个四面体映射到球面,并通过逆操作把被删除的顶点添加到球面上。Alexa[8]给出了一种很简单的球面参数化算法。首先把网格的所有顶点投影到模型的最小包围球面上;然后保持球面上6个顶点的位置不动,用离散Laplacian 平均算子来松弛球面的其他顶点,直到球面网格变成星型,达到球面参数化的目的。但是,这种先简单投影后松弛的方法,对形状比较复杂的模型需要多次循环。因此,时间代价很高。
1.2 内部点映射
为了得到曲面S的映射ϕ,必须定义对三角网格内部点的映射。Arvo[9]提出了一种从平面方形到球面的保积映射,Turk[10]提出了从方形到三角形的保积映射。将两者结合起来可以得到一个从三角形到球面的保积映射 Arvo·Turk-1。Buss-Fillmore[11]重新定义了对球面点A1,A2,Ak的重心组合方式。该算法需要多次迭代,但收敛速度较快。Emil[5]等总结了网格内部点映射的方法。
在本文中将凸组合方法应用到球面参数化中,结合 slerp算法参数化三角网格曲面。由于需要带边界的三角网格,因此先提出了一种快速分割封闭网格的办法。将得到的带边界的三角网格分别参数化,再利用 2-slerp算法映射三角网格内部点。
2 三角网络的球面参数化
凸组合参数化适用于带边界的三角网络。对于封闭的网络首先需要做切割处理。然后将网络边界映射到参数区域的凸边界上。
2.1 网格分割
寻找切割线,将三角网络切割成带边界的三角形网格,然后把网格的边界按边长比例逆时针映射到球面的凸区域边界上.凸组合参数化方法必须把网格的边界映射到球面的凸区域边界,否则结果可能无效。网络边界被映射到参数区域的凸边界上后,三角网格内部点在球面的对应点将由球面区域边界唯一表示。
切割线的选取对参数化的结果影响很大。为了减小参数化引起的扭曲和将网格均匀的参数化,可以通过寻找最长的顶点间最短路径。
从图论的角度看,三角网格可以视为带有权重的无向图,它的权重由边长来决定。因此,网格上任意两点间的最短路径可由Dijkstra算法或Floyd算法来获得
设得到的最短路径为ABCDEF。其中,AB为路径端点,BCDE为最短路径的中间点,如图1所示

图1 最短路径
获得初始切割线之后,需要将切割线展开成一个封闭的环,以将这个环作为参数域的边。对于最短路径中的每条边可以分拆一次得到环。如可将图1中的最短路径展开为

2.2 网格参数化
凸组合方法是指点的位置由其周围顶点位置决定。 设在三角网格中顶点vi相邻的顶点集为Ni={ ni1… nik},映射ϕ将vk映射到参数域中为 ∂ ( v k )( v k∈N i )则
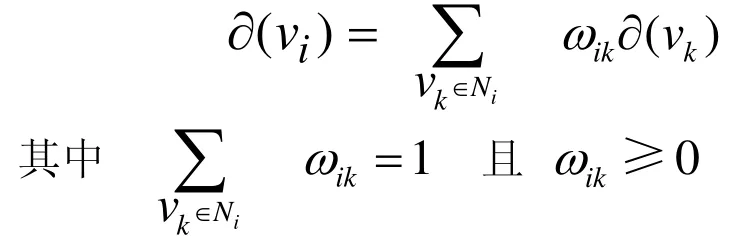
Floater[3-4]证明了该方法的保凸性。
选择映射ϕ,将bi到Sb。Sb为球面区域S边界,bi属于VB。三角网络的边界被映射到球面区域的边界上。
其次,对于所有的 vi ∈ V I,找到合适的正值 λij使得

由于方程左边全是网络中的内部顶点,右边点是网格中的外部顶点。所以方程可以写为
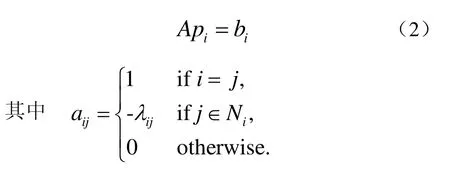
对于ijλ的选取,floater提出利用保角映射,可以减小参数化带来的形变。
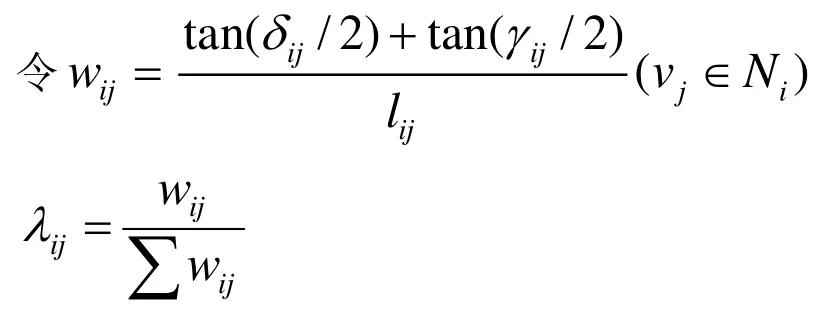
夹角(δij,γij)与边权(lij)的如图2所示。
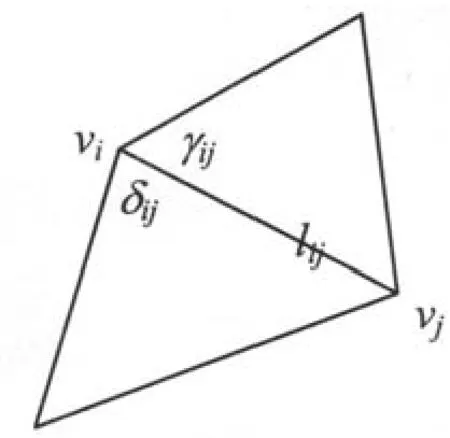
图2 夹角与边权
满足条件(1)的方程组中的矩阵A是非奇异的并且是稀疏的,构造了正值集合ijλ,通过解方程(1),可以得到了网格内部顶点的边界表示。可见,内部点的初始映射位置并不重要,因为它由边界点惟一确定。
Floater[3-4]证明了凸组合方法解的存在性和惟一性。利用凸组合参数化,可以将由边界分割得到的网络参数化到对应的球面区域边界上。封闭的三角网络便被全部映射到了球面上。
2.3 网格内部点的映射
三角网格被参数化到球面后,为了得到三角网格曲面的参数化,需要映射网格的内部点。设三角形的顶点为 { A,B,C},映射到球面上的对应点为A′=ϕ(A),B′=ϕ(B ),C′=ϕ(C)。对三角形中的点P=αA+βB+γC,其中α+β+γ=1,必须定义它在球面上的映射点P′=ϕ(P)。
在本文中,采用2-slerp算法[5]。在球面插值中,P ′ =s lerp(A′,B′,α)指寻找参数点P′使得
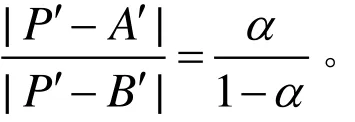
可以看出,slerp算法只能在一维空间中线性插值。为了将 slerp算法应用到三角形中,可以两次迭代slerp得到2-slerp。
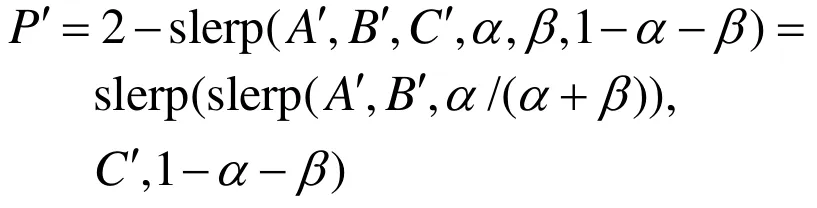
三角形内部点被映射后,三角网格曲面被完全映射到了球面上。
3 结果及讨论
本文将凸组合方法应用到球面参数化中,结合 slerp算法,提出了一种参数化三角网格球面的方法。在AMD双核2.21G,内存1G的PC机上,VC6.0的编译环境下实现了该方法。图3给出了一些动物模型参数化的结果。可以看出,在这4个模型中,三角网格曲面被较均匀的参数化。该算法在这些模型上应用得很好。可以直接将其应用到纹理映射、重新网格化、曲面拟合、morphing等技术中。
但在本文中,作者没有进行失真度量,以及根据失真分析的结果来优化算法。在以后的工作中,作者将失真分析考虑到模型的建立中,以得到更好的结果。

图3 凸组合参数化
[1]何援军. 计算机图形学[M]. 北京: 机械工业出版社,2006. 228-234.
[2]Alla Sheffer,Emil Praun, Kenneth Rose. Mesh parameter-ization methods and their applications [C]//Foundations and Trends® in Computer Graphics and Vision, 2006: 105-171.
[3]Floater M S. Parametrization and smoth approximation of surface triangulations [J]. Computer Aided Geometric Design, 1997, 14(3): 231-250.
[4]Floater M S. Mean value cordinates [J]. Computer Aided Geometric Design, 2003, 20(1): 19-27.
[5]Praun E, Hoppe H. Spherical parametrization and remeshing [C]//Computer Graphics Proceedings,Annual Conference Series, ACM SIGGRAPH, San Diego, 2003: 340-349.
[6]Craig Gotsman, Xianfeng Gu, Alla Sheff.Fundamentals of spherical parameterization for 3D meshes [J]. ACM Transactions on Graphics(TOG), 2003, 22(3): 358-363.
[7]Shapiro A, Ayellet T. Polyhed ron realization for shape transformation [J].The Visual Computer, 1998,14(8/9): 429-444.
[8]Alexa M. Merging po lyhed ron shapes with scattered features [J]. The Visual Computer, 2000, 16(1): 26-37.
[9]James Arvo. Stratified sampling of spherical triangles [C]//ACM SIGGRAPH, 1995: 437-438.
[10]TURK G. Generating random points in triangles,Graphics gems [M]. Academic Press, 1990. 649-650.
[11]BUSS S, AND FILLMORE J. Spherical averages and applications to spherical splines and interpolation [J].ACM Transactions on Graphics, 2001, 20(2): 95-126.
