基于脊波变换的旋转不变性纹理特征提取方法

韩 光， 赵春霞

（南京理工大学计算机学院，江苏 南京 210094）

纹理分析在过去的几十年里一直都是研究的热点问题，因为其在很多领域都起着十分重要的作用，例如，遥感分类[1]、图像检索[2]以及智能机器人导航[3]等领域。其中，纹理分类问题，特别是对于旋转了一定角度后的纹理图像的分类，在纹理分析中是一个既有挑战性又非常重要的问题。在文献中已经有很多关于旋转不变性的纹理特征提取方法被提出[4-5]。

脊波(Ridgelet)变换是最近才发展起来的一种信号表示方法[6]，这种变换可以分为两个阶段：Radon变换阶段和一维小波变换阶段，脊波变换可以能够解决线奇异问题，因此相对于只能解决点奇异的小波变换来说是更好的特征提取工具。Chen等[7]人首先提出了一种利用脊波变换来提取旋转不变性特征的方法，并且在字符和形状识别中表现良好。然而，该方法能产生高维特征，例如一幅64×64的字符图像，能够产生168维的特征，这使其在纹理分类中变得不可用，因为纹理图像的尺寸可能更大。Huang等[8]也提出了一种类似特征提取方法。Pan等[9]则提出了在脊波变换中使用频率 B-样条小波来提取旋转不变性特征的方法。

以上基于脊波变换的旋转不变性纹理特征是经过一维小波变换后，在每个频率子波段中独立提取的，并没有考虑到同一分解尺度下高、低频子波段之间的相互关系。然而这种关系是的确存在的，即使使用正交化小波进行分解，同一分解尺度下高、低频子波段之间的相互关系也是存在的。Portilla 和 Simoncelli[10]已经证明如果没有这些子波段间相互关系的知识，纹理的准确重构是不可能的。Wang等[11]也将这种关系用于纹理分类，该方法是在小波包变换中利用线性回归模型来评估子波段间关系，并将回归模型的系数作为特征。Hiremath等[12]则在小波变换后的图像中计算共生直方图来提取不同频率子波段之间的关系作为特征，并且在纹理分类和字符识别中表现良好。

基于以上分析，本文提出了一种新的基于脊波变换的旋转不变性纹理特征提取方法。该方法是先将图像经过脊波变换得到脊波变换系数矩阵。然后，对于上述矩阵中的频率系数，采用一种直方图的形式来提取特征，用以评估高、低频子波段之间系数的相互关系，对这些关系特征数据以及在每个子波段中提取的特征沿方向θ进行一维傅里叶变换并取其幅值，从而得到本文所提出的旋转不变性纹理特征。实验表明，本文方法可靠有效。

1 脊波变换

1.1 连续Ridgelet变换[13]

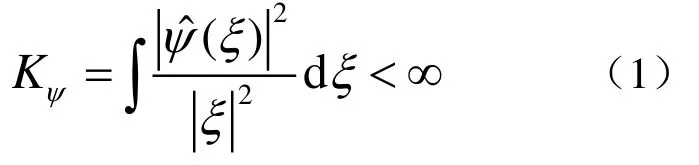
则对于参数集γ，定义2R →R函数

则称γψ为由容许条件生成的Ridgelet函数。其中，a称为Ridgelet的尺度参数，u表示方向，b为位置参数。

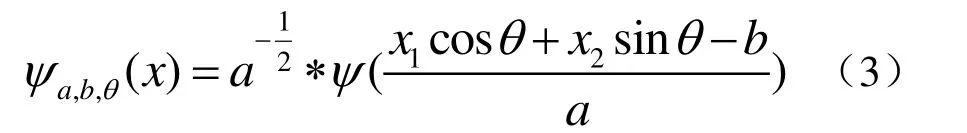
其中 ψ(x)为一维Wavelet函数，称变换

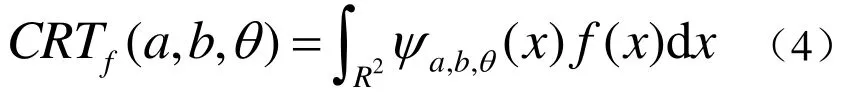
1.2 脊波变换的数字实现

由脊波变换与Radon变换的关系可知，为了实现脊波变换，第一步首先要计算 Radon变换Rf(θ,t)，然后对投影切片 Rf(θ,⋅)进行一维小波变换，最终得到Ridgelet变换系数矩阵。

由投影切片定理，如下式(7)所示

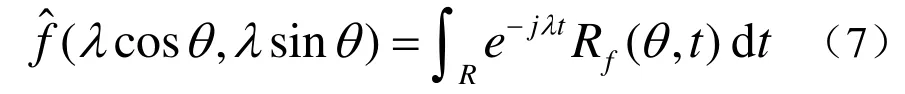
2 在脊波域中的旋转不变性纹理提取方法

2.1 纹理图像的脊波变换

假设给定一幅 N×N的纹理图像，首先对该图像进行二维傅里叶变换，然后在变换后的图像中央选择一个圆盘区域，并在方向[0°，180°]内等间隔角度进行频率抽样，从而得到映射切片。根据文献[5]，映射切片的总数在(π/2)N～πN时，可产生较好的分类结果，这里选择映射切片的总数为2N，即频率抽样的间隔角度为180°/2N。经过Radon变换后，在每个映射切片上应用一维小波变换，可得到脊波变换系数矩阵。从脊波变换系数矩阵可以看出，给定图像的旋转将会导致在每个矩阵中列指数的循环平移。上述过程可由图1所示。

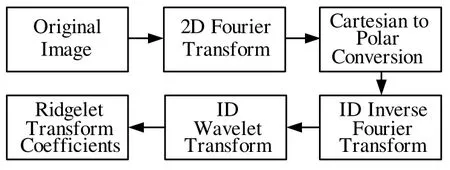
图1 脊波变换流程图

2.2 脊波变换后高、低频子波段间关系特征的提取

Hiremath等人[12]在二维图像中进行小波变换后，用共生直方图来提取不同频率子波段之间的关系，但这种方法不能够直接用于脊波变换后的频率系数中，本文对Hiremath的方法进行了简化和改进，使其能够用于提取脊波变换后各频率子波段之间的关系。对于一幅纹理图像，通过上述脊波变换得到脊波变换系数矩阵，该矩阵的列坐标是采样方向θ，行坐标是频率系数长度。其中，在对投影切片进行一维小波变换时，每分解一层，便可产生一个近似(A)和一个细节(V)系数矢量（不同于二维小波变换，会形成3个方向的细节系数矩阵）。近似(A)和细节(V)系数矢量分别对应的是低、高频子波段。脊波变换后高、低频子波段间关系特征的提取算法如下：

（1）对脊波变换系数矩阵按列平分成 M组，每组包含n列，这样就得到M组长度为m（对投影切片进行一维小波变换后的频率系数长度），宽度为n的近似系数矩阵Aq和细节系数矩阵Vq，其中，1≤q≤M。

（2）直方图构建。在 Aq中的小波系数 xij对应在 Vq中的系数 yij，1≤i≤m，1≤j≤n，其上下最近邻ak和hk展示如图2所示，k=1、2分别代表上、下方向。

图2 在Aq和Vq中xij和yij的上下最近邻

直方图构建的伪代码如下（见表1）：

表1 直方图构建算法

对于每一对(Aq, Vq)，通过上述算法将产生4个直方图H，每个方向两个。

（3）规范化累积直方图

将H设为256等级值，即

这里，ni是每个等级值的占有数目。然后对于这256个等级值的累计占有数目进行计算并使其规范化，从而得到规范化的累积直方图。

所有在步骤(2)中得到的直方图都要再经过上述处理。

（4）特征提取

对于规范化的累积直方图NCH，可得到序列对 ( y0, x0), ( y1, x1),…,( y255, x255)，其中，yi在 0到1之间，xi在0到255之间。将这些序列对利用最小均值的方法进行直线拟合，并计算其斜率k和偏移量h

对于每一对 (Aq, Vq)，可得到4个直方图，而每个直方图可以给出了2个特征，也就是说对于每一对(Aq, Vq)共可得到2（特征）×4（直方图）=8个特征。

2.3 旋转不变性的纹理特征提取

对每个投影切片进行3尺度的小波分解后得到脊波变换系数矩阵，并在该矩阵中进行旋转不变性纹理特征提取，具体过程如下：

（1）首先对脊波变换系数进行分组，将该矩阵中列平分成16组。例如，组1包含了给定矩阵的1-16列，组2包含了给定矩阵的17-32列等。

（2）在每组系数中，分别计算近似和细节系数的均值和方差如下所示

这里的Mi是在第i组中系数的个数，c是第i组中的系数。

（3）按2.2节中的方法计算每个分解尺度子波段间的关系特征k、h。

3 实验结果及其分析

该实验使用了以下两个数据库来评估本文算法的性能，第一个数据库是来自麻省理工学院的视觉纹理数据库(VisTex)，另一个是Brodatz数据库。 其中，VisTex是关于真实世界场景的纹理库，而Brodatz则是标准的纹理库，并且这两个数据库都是可以公开获得的。同时将本文提出的算法与Pan的方法[9]和Pietikäinen的LBP特征提取法[15]进行实验对比，上述两种对比方法分别称为方法一和方法二。该实验使用了 K近邻(K Nearest-Neighbour, K-NN)分类器用于纹理分类，K值被分别设置为 1、3、5、7和 9。这里的 K值是指将一个测试数据分类为与它最接近的 K个近邻训练数据中出现最多的那个类别，为了不产生分类模糊，K一般为奇数。在实验中作者发现当 K值超过 10以后，分类正确率(Correct Classification Percentages，CCP)下降明显，所以这里只给出10以内K值的分类结果。

数据集1是从VisTex数据库中随机挑选的20幅纹理图像，其大小为512×512，如图3所示。每幅图像都被分割成 16个无重叠的大小为128×128的子图像，这样共可得到320(20×16)幅子图像用做训练集。将每幅图像按一定角度旋转，旋转角度从 10°到 160°，间隔 10°，然后在每个旋转图像的中心区域分割出 4幅无重叠的128×128的子图像。这样可获得 1280(20×16×4)幅子图像用作测试集。

图3 VisTex数据库中的20幅纹理图像

数据集2是从Brodatz数据库中随机挑选的30幅纹理图像，其大小为640×640，如图4所示。每幅图像被分割成25个128×128大小的子图像，因此共有750(30×25)幅子图像用作训练集。测试集的创建方法同数据集 1中方法一样，有1920(30×16×4)幅子图像用做测试集。

图4 Brodatz数据库中的30幅纹理图像

表2为使用不同类型小波基时的本文方法与现有方法在数据集 1上的分类正确率(Correct Classification Percentages，CCP)对比。由表可见，对使用同一类小波基， CCP随K的增加没有明显的变化；对于同一K值，使用不同类型的小波基时，CCP也无明显变化，只是使用Rbio3.7小波基时的 CCP要稍高于其它几种小波基。从表中也可看出，本文方法使用表中各类型小波基时的CCP(除及个别外)，要高于文献方法一，远高于文献方法二，这同时也验证了本文所提出的旋转不变性纹理特征的有效性。

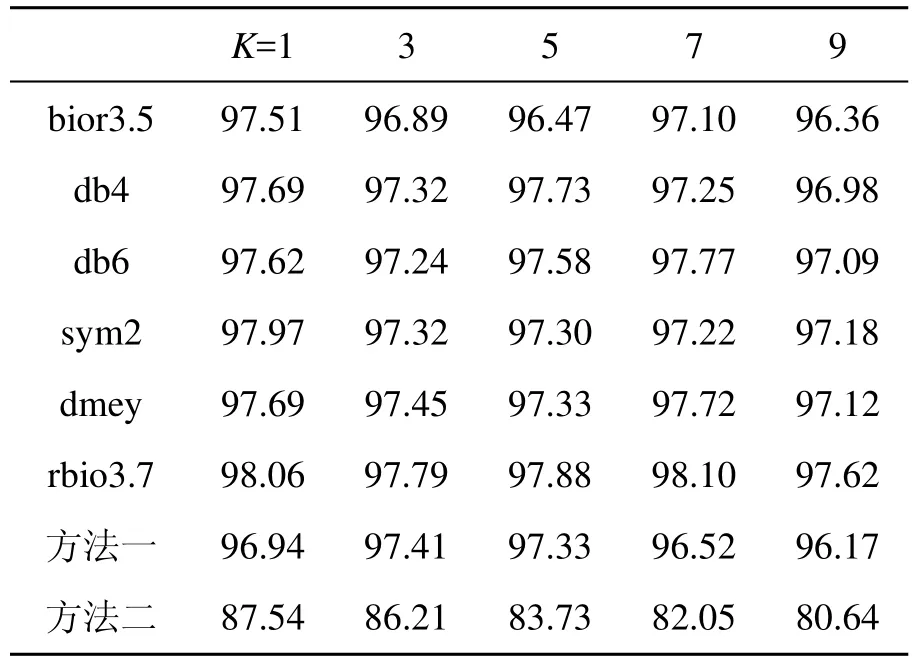
表2 使用不同小波基时的本文方法与现有方法在数据集1上的CCP对比(%)

表3为使用不同类型小波基时的本文方法与现有方法在数据集2上的CCP对比。由表可知，对于同一类小波基，CCP随K的增加略微呈上升趋势；对于同一K值，使用不同类型的小波基时，CCP变动幅度较大，使用 Rbio3.7小波基时的CCP要高于使用其它几种小波基的结果，尤其要高于使用 bior3.5小波基时的结果。这说明该数据集对使用何种类型的小波基较敏感，但从结果来看，使用rbio3.7小波基时的CCP仍然是较高的。但与表2 相比，CCP普遍有所下降，原因除了数据集2中的图像增多外，在于该数据集中的图像纹理相似性程度要高于数据集 1。使用bior3.5、db4、db6、sym2及dmey6的CCP比使用方法一的CCP要低，除Bior3.5外均高于方法二。但是当本文方法使用rbio3.7小波基时的CCP要高于上述两种文献方法。

4 结 论

本文提出了一种新的基于脊波变换的旋转不变性纹理特征提取方法。该方法的特点是在脊波变换后所形成的每个频率子波段中独立提取特征的基础上，融合了同一分解尺度下高、低频子波段之间的关系特征。将本文所提出方法与两种最近才发展起来的用于旋转不变性纹理分类的方法进行了对比实验，结果表明本文的方法能够取得更好的分类结果。如何利用脊波变换提取的旋转不变性特征在真实的场景图像中进行地形分类，是本文下一步的研究方向。

[1]Kandaswamy U, Adjeroh D A, Lee M C. Efficient texture analysis of SAR imagery [J]. IEEE Transaction on Geoscience and Remote Sensing, 2005, 43(9):2075-2083.

[2]Giacinto G, Roli F. Bayesian relevance feedback for content-based image retrieval [J]. Pattern Recognition,2004, 37(7): 1499-1508.

[3]Manduchi R, Castano A, Talukder A, et al. Obstacle detection and terrain classification for autonomous off-road navigation [J]. Autonomous Robots, 2005, 18:81-102.

[4]Pun C M, Lee M C. Log-polar wavelet energy signatures for rotation and scale invariant texture classification [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5):590-603.

[5]Jafari-Khouzani K, Soltanian-Zadeh H. Rotation invariant multi-resolution texture analysis using radon and wavelet transforms [J]. IEEE Transactions on Image Processing, 2005, 14(6): 783-795.

[6]Candes E J, Donoho D L. Ridgelets: a key to higherdimensional intermittency [J]. Philosophical Transactions of the Royal Society of London, Series A,1999, 357(1760): 2495-2509.

[7]Chen G Y, Bui T D, Krzyzak A. Rotation invariant pattern recognition using ridgelet, wavelet cycle-spinning, and fourier features [J]. Pattern Recognition, 2005, 38(12): 2314-2322.

[8]Huang K, Aviyente S. Rotation invariant texture classification with ridgelet transform and fourier transform [C]//Proceeding of IEEE International Conference on Image Processing, 2006: 2141-2144.

[9]Pan W, Bui T D, Suen C Y. Rotation invariant texture classification by ridgelet transform and frequencyorientation space decomposition [J]. Signal Processing,2008, 88: 189-199.

[10]Portilla J, Simoncelli P E. A parametric texture model based on joint statistics of complex wavelet coefficients [J]. International Journal of Computer Vision, 2000, 40(1): 49-70.

[11]Wang Z Z, Yong J H. Texture analysis and classification with linear regression model based on wavelet transform [J]. IEEE Transactions on Image Processing, 2008, 17(8): 1421-1430.

[12]Hiremath P S, Shivashankar S. Wavelet based co-occurrence histogram features for texture classification with an application to script identification in a document image [J]. Pattern Recognition Letters, 2008, 29: 1182-1189.

[13]Candes E J. Ridgelet theory and applications [D].Stanford University, 1998.

[14]Starck J, Candes E J, Donoho D L. The curvelet transform for image denoising [J]. IEEE Transaction on Signal Processing, 2002, 11(6): 670-684.

[15]Pietikäinen M, Nurmela T, Mäenpää T, et al.View-based recognition of real-world textures [J].Pattern Recognition, 2004, 37(2): 313-323.