基于八叉树编码的点云数据精简方法

邵正伟， 席 平

（北京航空航天大学机械工程及自动化学院，北京 100191）

在逆向工程中，非接触式测量方法获取的被测物的数据一般具有无序、海量的特点[1]。无序的特点是指每个数据点只具有三维坐标值的信息，而没有明确的空间邻域信息，不利于邻域数据点的搜索，而邻域数据点的搜索速度正是影响散乱数据处理和曲面重构效率的主要因素之一。海量的特点是指测量数据过密，这不但会影响曲面的重构速度，而且在重构曲面的曲率较小处还会影响曲面的光顺性。因此，在进行曲面重构前，需要建立数据的空间邻域关系和精简数据。文中应用八叉树编码的空间邻域划分方法，并在此基础上提出了一种新的点云数据均匀精简方法。

1 点云精简方法

近年来，人们做了很多关于数据精简方面的研究，主要包括曲率精简和均匀精简两类方法。在曲率精简方法中，洪军[2]先利用包围盒法构造分割面，然后利用分割面将点云处理成扫描线结构，再利用角度、弦高联合准则法逐线精简；周绿[3]使用了抛物面拟合法求解局部曲率，再根据曲率偏差对点云进行精简。在均匀精简方法中，万军[4]通过以某一点定义采样立方体，求立方体内其余点到该点的距离，再根据平均距离和用户指定保留点的百分比进行精简，该方法由于没有预先对点云数据划分空间邻域，在检索采样立方体过程中，需要对全部点云数据进行判断，因此处理海量数据时计算量较大，且不能根据指定的点距精简点云。

针对以上方法的不足，文中提出新的均匀精简方法的原理是：

（1）根据指定的点距，应用八叉树编码法对点云进行空间邻域划分，把点云数据的空间包围盒（最小外接立方体）划分为多个指定点距d0边长的子立方体，具体方法见2节；

（2）分别对每个子立方体进行数据精简，如图1所示，若在划分后的某两个相邻子立方体中存在8个数据点p1～p8，保留每个子立方体中距中心点最近的点p3和p7。由于相邻子立方体中心点的距离为d0，所以精简后点云中p3和p7之间的距离也近似为d0。

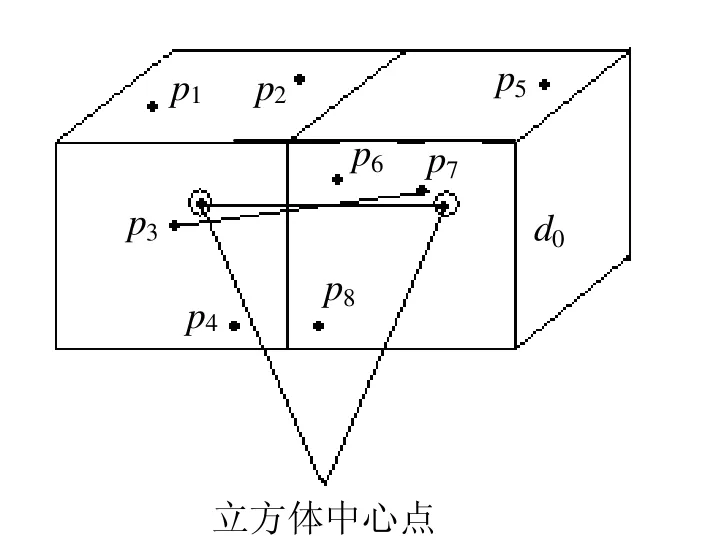
图1 点云子立方体

2 空间邻域划分

在对散乱数据进行精简、滤波、特征提取等处理过程中，需要获取数据点在其型面对应点处的单位法矢、微切平面及曲率值等信息，这就需要搜索数据点的k近邻，即在数据点集中寻找k个与该点欧氏距离最近的点。一般的搜索方法就是穷举法：计算某点与点集中其余点的欧氏距离，并按从小到大排序，选取排在前面的K个点为该点的k个最近邻点。对于海量点数据，这种搜索方法耗时极大，因此，为点云建立良好的空间邻域结构是提高数据点 k近邻搜索速度的关键。

下面介绍一种在逆向工程中常采用的空间邻域划分方法——八叉树法。

2.1 八叉树法原理

八叉树结构是区域四叉树向三维空间的推广，是通过递归分割点云空间的方式实现的。首先构造点云数据的空间包围盒（外接立方体），并把它作为数据点云拓扑关系的根模型；再将外接立方体分割成大小相同的8个子立方体，每个子立方体均视为根节点的字节点；如此递归分割，直至最小子立方体的边长等于给定的点距，将点云空间hu划分为2的幂次方个子立方体。

在八叉树划分过程中，子立方体的编码与其所在的位置有关[5]。如图2所示，规定：在x轴上位于x中分面右侧的子节点编码均比左侧相邻节点编码加1；在y轴上位于y中分面前侧的均比后侧的相邻节点位置码增加2；在z轴上位于z中分面上侧的均比下侧的相邻节点位置码增加4。

图2 八叉树空间划分模型

对于一个正立方体包围盒空间进行递归八等分，假设剖分层数为n，则八叉树空间模型可以用n层八叉树表示，八叉树空间模型中的每个立方体与八叉树中的结点一一对应，它在八叉树空间模型中的位置可由对应结点的八叉树编码Q表示

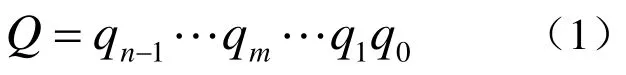
其中 qm为八进制数表示该节点在其兄弟节点之间的序号，而qm+1表示qm节点的父节点在其同胞兄弟节点间的序号。这样，从q0到qn-1完整地表示出八叉树中的每个叶子节点到树根的路径。

2.2 点云数据编码

点云数据编码的步骤为：

（1）确定点云八叉树剖分层数n，满足

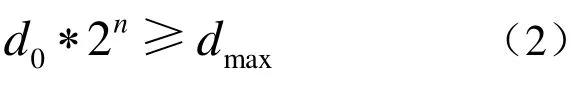
其中 d0为精简的指定点距，dmax为点云包围盒的最大边长。

（2）确定点云数据点所在子立方体的编码，假设数据点 P ( x , y,z )，所在子立方体的空间索引值为(i, j,k )，Q为与子立方体相对应的结点的八叉树编码。三者的关系可由公式(3)～(5)表示[6-8]

其中 (xmin,ymin,zmin)表示与根节点对应的包围盒的最小顶点坐标值，[…]为取整操作符。

将索引值(i , j,k )转换为2进制表示方式

则子立方体对应的八叉树编码可由公式(1)表示。同时，如果已知子立方体对应的八叉树编码Q，也可以反求出数据点所在子立方体的空间索引值(i , j,k )

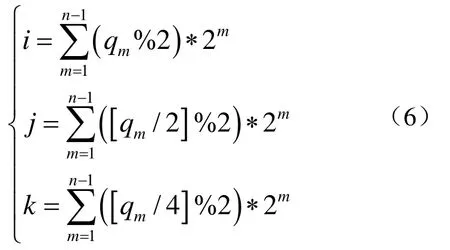
其中 (qm%2)表示对qm除以 2所得余数，[qm/2]表示对qm除以2所得结果取整数。

在搜索数据点的k近邻时，可在数据点所在的子立方体及其周围相邻的 26个子立方体中搜索。若空间某子立方体的索引值为(i , j,k )，则其周围 26个子立方体的索引值可由(i ±δ, j ±δ,k±δ)表示，δ ∈ {0 , 1}。因此，经过八叉树划分后的点云，只需要在局部进行k近邻搜索，明显提高了搜索速度。

3 应用实例

基于八叉树编码的均匀精简算法的流程如图3所示，在UG软件平台上使用C++语言二次开发了点云数据的预处理模块，如图4所示。并针对涡轮叶片模具的测量数据进行精简，图5所示为初始测量点云，包含数据点24500个，图6所示为指定精简距离为 2mm的精简后点云，包含数据点 4607个，精简后的点云在空间分布均匀，适合数据的后续处理。

图3 算法流程图

图4 点云数据的预处理模块

图5 初始测量点云

图6 精简后点云

4 结 论

本文提出的点云精简算法能对逆向工程测量的海量数据做出快速有效的精简，算法具有以下特点：

（1）从空间整体角度考虑点云的均匀精简，精简效果较好；

（2）由于精简前对点云进行了空间划分，因此算法简洁、高效；

（3）用户通过设定精简点距，可以灵活实现点云精简。

[1]孙肖霞, 孙殿柱, 李延瑞, 等. 反求工程中测量数据的精简算法[J]. 机械设计与制造, 2006, (8): 37-38.

[2]洪 军, 丁玉成, 曹 亮, 等. 逆向工程中的测量数据精简技术研究[J]. 西安交通大学学报, 2004, 38(7):661-664.

[3]周 绿, 林 亨, 钟跃先, 等. 曲面重构中测量点云精简方法的研究[J]. 中国制造业信息化, 2004, 33(5):102-104.

[4]万 军, 鞠鲁粤. 逆向工程中数据点云精简方法研究[J]. 上海大学学报, 2004, 10(1): 26-29.

[5]张传明, 潘 懋, 徐绘宏. 基于分块混合八叉树编码的海量体视化研究[J]. 计算机工程, 2007, 33(14):33-35.

[6]范 茵, 汪德宗. 八叉树编码的三维物体截面之比计算[J]. 数据采集与处理, 1999, 14(1): 47-51.

[7]赵 强. 基于BSP树的点云精简方法研究[D]. 西安:西北工业大学, 2007.

[8]孙肖霞. 基于UGII的反求工程数据处理技术研究与系统开发[D]. 淄博: 山东理工大学, 2006.